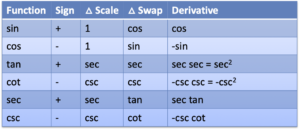
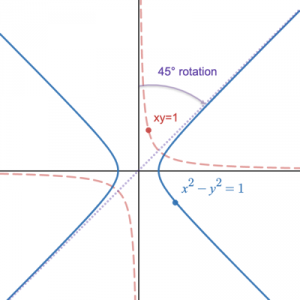
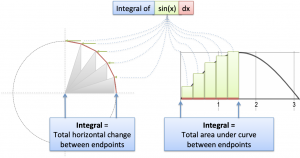
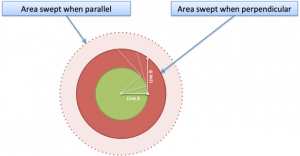
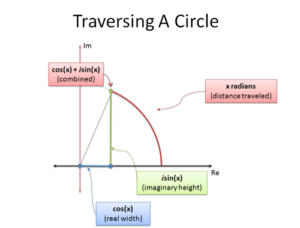
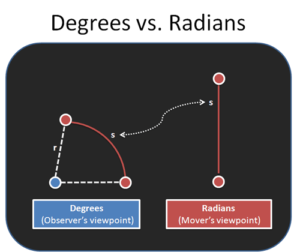
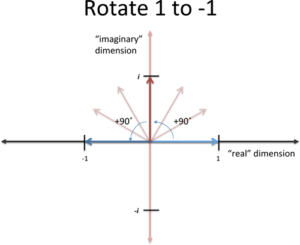
Why Is Better Explained Different?
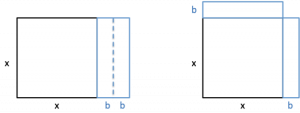
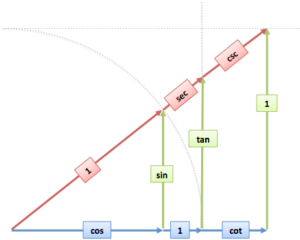
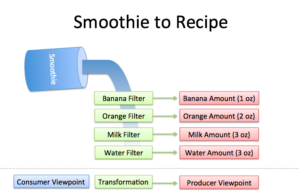
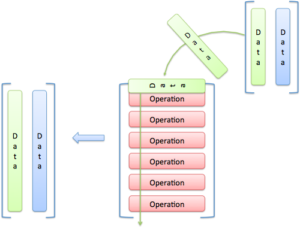
Most lessons offer low-level details in a linear, seemingly logical sequence. Better Explained focuses on the big picture — the Aha! moment — and then the specifics. Here’s the difference:

I know which approach keeps my curiosity and enthusiasm. The learning strategy is the ADEPT Method:
Learning isn’t about memorizing facts to pass a test. It’s about unlocking the joy of discovery when an idea finally makes sense. If this approach resonates with you, welcome aboard.
About Kalid Azad
I enjoyed math until a poorly-taught class nearly destroyed that passion. A last-minute Aha! moment showed me math could make sense, even be enjoyable, when presented with:
- A friendly, curious attitude
- A mix of intuitive and technical understanding
- A focus on lasting insight
I share explanations that helped, hoping they help you too. I’m thrilled that Better Explained now reaches millions every year, and has appeared in blogs for the New York Times and Scientific American. Read more…