Multiplication is a wonderful little operation. Depending on the context, it can
- Scale or stretch a number
- Rotate a vector, without needing sine or cosine
And today we’ll see yet another use: listing combinations.
Revisiting multiplication has a few uses:
- It demystifies other parts of math. The binomial theorem, Boolean algebra (used in computer circuits) and even parts of calculus become easier with a new interpretation of “multiplication”.
- It keeps our brain fresh.Math gives us models to work with, and it’s good to see how one model can have many uses. Even a wrench can drive nails, once you understand the true nature of “being a hammer” (very Zen, eh?).
The long multiplication you learned in elementary school is quite useful: we can find the possibilities of several coin flips, for example. Let’s take a look.
You’ve Been Making Combinations All Along
How would you find 12 × 34? It’s ok, you can do it on paper:

“Well, let’s see… 4 times 12 is 48. 3 times 12 is 36… but it’s shifted over one place, so it’s 360. Add 48 and 360 and you get… uh… carry the 1… 408. Phew.”
Not bad. But instead of doing 12 × 34 all at once, break it into steps:
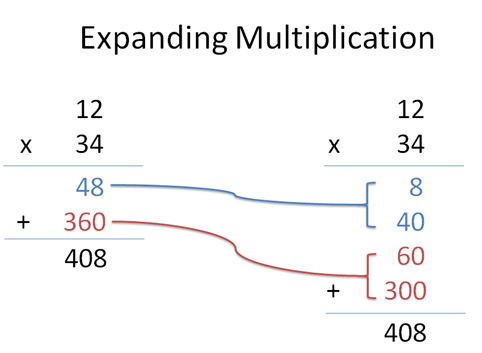
What’s happening? Well, 4 × 12 is actually “4 x (10 + 2)” or “40 + 8″, right? We can view that first step (blue) as two separate multiplications (4×10 and 4×2).
We’re so used to combining and carrying that we merge the steps, but they’re there. (For example, 4 × 17 = 4 x (10 + 7) = 40 + 28 = 68, but we usually don’t separate it like that.)
Similarly, the red step of “3 × 12″ is really “30 × 12″ — the 3 is in the tens column, after all. We get “30 x (10 + 2)” or “300 + 60″. Again, we can split the number into two parts.
What does this have to do with combinations? Hang in there, you’ll see soon enough.
Curses, Foiled Again
Take a closer look at what happened: 12 × 34 is really (10 + 2) x (30 + 4) = 300 + 40 + 60 + 8. This breakdown looks suspiciously like algebra equation (a + b) * (c + d):

And yes, that’s what’s happening! In both cases we’re multiplying one “group” by another. We take each item in the red group (10 and 2) and combine it with every element of the blue group (30 and 4). We don’t mix red items with each other, and we don’t mix blue items with each other.
This combination technique is often called FOIL (first-inside-outside-last), and gives headaches to kids. But it’s not a magical operation! It’s just laying things out in a grid. FOIL is already built into the way we multiply!
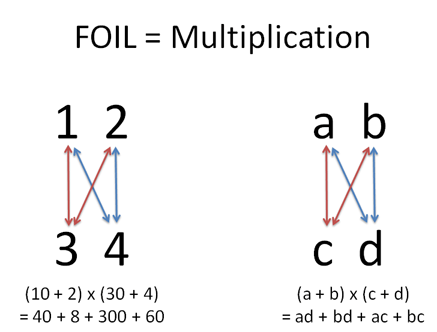
When doing long multiplication, we “know” we’re not supposed to multiply across: you don’t do 1 × 2, because they’re in the same row. Similarly, you don’t do a x b, because they’re in the same parenthesis. We only multiply “up and down” — that is, we need an item from the top row (1 or 2, a or b) and an item from the bottom row (3 or 4, c or d).
Everyday multiplication (aka FOIL) gives us a way to crank out combinations of two groups: one from group A, another from group B. And sometimes it’s nice having all the possibilities as an equation.
Examples Make It Click
Let’s try an example. Suppose we want to find every combination of flipping a coin twice. There’s a few ways to do it, like using a grid or decision tree:
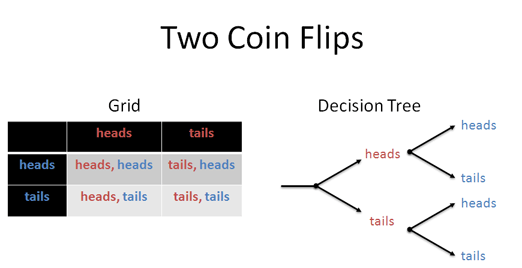
That’s fine, but let’s be different. We can turn the question into an equation using the following rules:
- addition = OR. We can get heads OR tails: (h+t)
- multiplication = AND. We have a first toss AND a second toss: (h+t) * (h+t)
Wow! How does this work?
Well, we really just want to crank out combinations, just like doing (a+b) * (c+d) = ac + bc + ad + bd. Looking carefully, this format means we pick a OR b, and combine it with one of c OR d.
When we see an addition (a+b), we know it means we must choose one variable: this OR that. When we see a multiplication (group1 * group2), we know it means we take one item from each: this AND that.
The shortcuts “AND = multiply” & “OR = add” are simply another way to describe the relationship inside the equation. (Be careful; when we say three hundred and four, most people think 304, which is right too. This AND/OR trick works in the context of describing combinations).
So, when all’s said and done, we can turn the sentence “(heads OR tails) AND (heads OR tails)” into:
![]()
And just for kicks, we can multiply it out:
![]()
The result “h2 + 2ht + t2” shows us every possibility, just like the grids and decision trees. And the size (coefficient) of each combination shows the number of ways it can happen:
- h^2: There’s one way to get two heads (h2 = hh = heads AND heads)
- 2ht: There’s two ways to get a head and tails (ht, th)
- t^2: There’s one way to get two tails (tt)
Neato. The sum of the coefficients is 1 + 2 + 1 = 4, the total number of possibilities. The chance of getting exactly one heads and one tails is 2/4 = 50%. We figured this out without a tree or grid — regular multiplication does the trick!
Grids? Trees? I Figured That Out In My Head.
Ok, hotshot, let’s expand the scope. How many ways can we get exactly 2 heads and 2 tails with 4 coin flips? What’s the chance of getting 3 or more heads?
Our sentence becomes: “(heads OR tails) AND (h OR t) AND (h OR t) AND (h OR t)”
![]()
Looking at the result (it looks hard but there are shortcuts), there are 6 ways to get 2 heads and 2 tails. There’s 1 + 4 + 6 + 4 + 1 = 16 possibilities, so there’s only a 6/16 = 37.5% chance of having a “balanced” result after 4 coin flips. (It’s a bit surprising that it’s much more likely to be uneven than even).
And how many ways can we get 3 or more heads? Well, that means any components with h3 or h4: 4 + 1 = 5. So we have 5/16 = 31.25% chance of 3 or more heads.
Sometimes equations are better than grids and trees — look at how much info we crammed into a single line! Formulas work great when you have a calculator or computer handy.
But most of all, we have another tool in our box: we can write possibilities as equations, and use multiplication to find combinations.
Where Next?
There’s a few areas of math that benefit from seeing multiplication in this way:
Binomial Theorem. This scary-sounding theorem relates (h+t)^n to the coefficients. If you’re clever, you realize you can use combinations and permutations to figure out the exponents rather than having to multiply out the whole equation. This is what the binomial theorem does. We’ll cover more later — this theorem shows up in a lot of places, including calculus.
Boolean Algebra. Computer geeks love converting conditions like OR and AND into mathematical statements. This type of AND/OR logic is used when designing computer circuits, and expressing possibilities with equations (not diagrams) is very useful. The fancy name of this technique is Boolean Algebra, which we’ll save for a rainy day as well.
Calculus. Calculus gets a double bonus from this interpretation. First, the binomial theorem makes working with equations like x^n much easier. Second, one view of calculus is an “expansion” of multiplication. Today we got practice thinking that multiplication means a lot more than “repeated addition”. (“12 × 34″ means 12 groups of 34, right?)
More advanced combinations. Let’s say you have 3 guests (Alice, Bob, and Charlie) and they are bringing soda, ice cream, or yogurt. Someone knocks at the door — what are the possibilities? (a + b + c) * (s + i + y). The equation has it all there.
So you can teach an old dog like multiplication new tricks after all. Well, the tricks have always been there — it’s like discovering Fido has been barking poetry in morse code all this time.
And come to think of it, maybe we’re the animal that learned a new trick. The poetry was there, staring us in the face and we just didn’t recognize it (12 × 34 is based on combinations!). I know I had some forehead-slapping moments after seeing how similar combinations and regular multiplication really were.
Happy math.
