Understanding Why Complex Multiplication Works

Seeing imaginary numbers as rotations was one of my favorite aha moments:

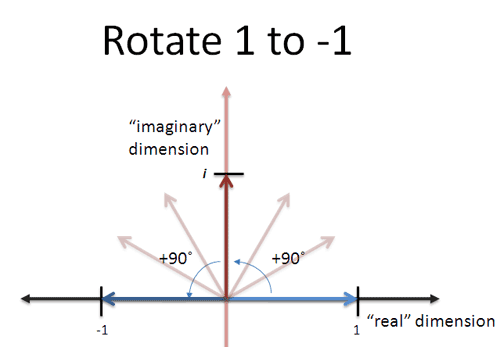
i, the square root of -1, is a number in a different dimension! Once that clicks, we can use multiplication to "combine" rotations of two complex numbers:

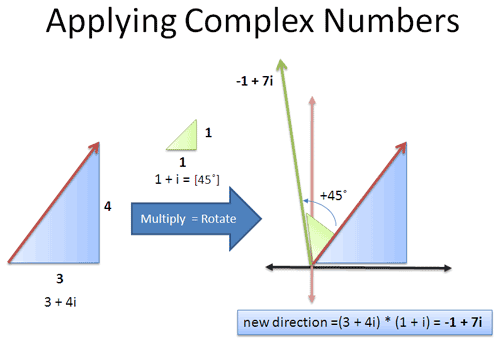
Yowza, did that ever blow my mind: add angles without sine or cosine! Unfortunately, I didn't have an intuitive grasp of why this worked. Let's fix that!

The Boring Explanation: How?

Here's the common explanation of why complex multiplication adds the angles. First, write the complex numbers as polar coordinates (radius & angle):

$\displaystyle{ r1(\cos(a) + i\sin(a)) \cdot r2 (\cos(b) + i\sin(b)) }$

Next, take the product, group by real/imaginary parts:

$\displaystyle{ = (r1 \cos(a) \cdot r2 \cos(b) - r1 \sin(a) \cdot r2 \sin(b))}$ $\displaystyle{ + i (r1 \cos(a) \cdot r2 \sin(b) + r2 \cos(b) \cdot r1 \sin(a)) }$

$\displaystyle{ = r1 \cdot r2[(\cos(a) \cdot \cos(b) - \sin(a) \cdot \sin(b))}$ $\displaystyle{ + i (\cos(a) \cdot \sin(b) + \cos(b) \cdot \sin(a))] }$

Lastly, notice how this matches the sine and cosine angle addition formulas:

$\displaystyle{ \cos(a+b) = \cos(a) \cdot \cos(b) - \sin(a) \cdot \sin(b) }$ $\displaystyle{ \sin(a+b) = \cos(a) \cdot \sin(b) + \cos(b) \cdot \sin(a) }$

And there you have it! What's that? You don't intuitively think in terms of sine and cosine expansions? Too bad, the math checks out!

...

Still here? Good. The problem is we've lost the magic: it's like saying two poems are similar because we analyzed the distribution of letters. Accurate but unsatisfying!

I like sine as much as anyone, but the details come after seeing the relationship click.

The Fun Explanation: Why!

What's our goal again? Oh yes -- to see why we can multiply two complex numbers and add the angles.

First, let's figure out what multiplication does:

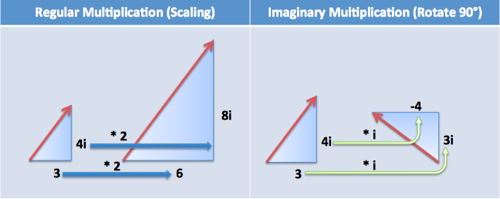
Regular multiplication ("times 2") scales up a number (makes it larger or smaller)
Imaginary multiplication ("times i") rotates you by 90 degrees

And what if we combine the effects in a complex number? Multiplying by (2 + i) means "double your number -- oh, add in a perpendicular rotation".

Quick example: $4 \cdot (3+i) = 4 \cdot 3 + 4 \cdot i = 12 + 4i$

That is, take our original (4), make it 3 times larger (4 * 3) and then add the effect of rotation (+4i). Again, if we wanted only rotation, we'd multiply by "i". If we wanted only scaling we'd multiply by plain old 3. A complex number (a + bi) has both effects.

Visualizing Complex Multiplication

That was easy -- a real number (4) times a complex (3+i). What about two complex numbers ("triangles"), like $(3 + 4i) \cdot (2 + 3i)$?

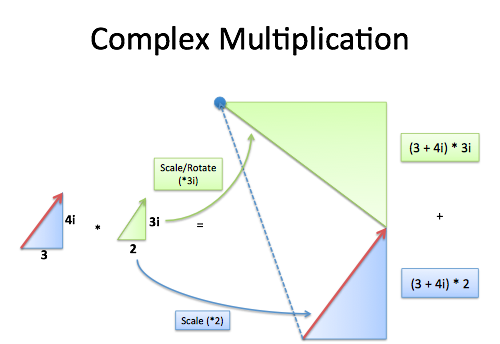
Now we're talking! I see this as "Make a scaled version of our original triangle (times 2) and add a scaled/rotated triangle (times 3i)". The final endpoint is the new complex number.

But... I love alternate explanations! Here's another:

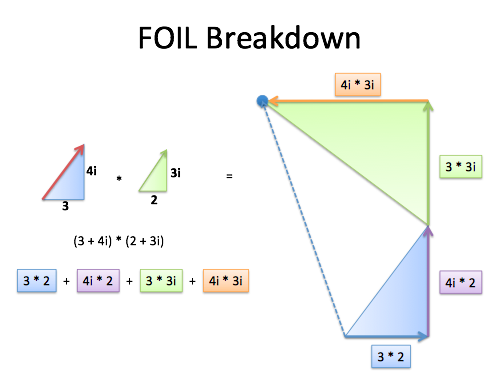
Instead of grouping the multiplication by triangle, we analyze each part of the FOIL (first, outside, inside, last). Adding each component takes us along a path and ends in the same spot!

But What About the Angles?

Ah yes, the angles. It looks like we're adding the angles, but can we be sure?

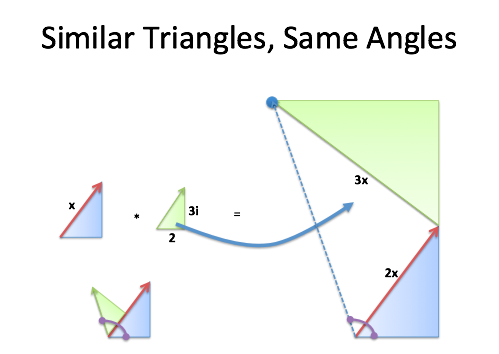
Captain Geometry to the rescue! Oh, how I've missed you from 9th grade. Is the result (dotted blue line) at the same angle as plopping the triangles on each other?

In the normal case, we start with a triangle (3 + 4i) and plop on the other (2 + 3i) to get the combined angle.

After the multiplication, we start with a scaled triangle (2x) and plop on another scaled triangle (times 3i). Even though it's larger, similar triangles have the same angles -- they're just bigger (but don't ask about its size, ok?).

We scaled up the original triangle (no change in angle) and "plopped on" another scaled triangle (no change in angle), so the result is the same! I love seeing this come together -- we scale up, rotate out, and boom -- we're at the combined angle. This isn't about "imaginary numbers" -- it's a way to combine triangles without trigonometry!

Side Effects May Include Scaling

Notice how we're making larger copies of our original triangle and adding them together. What's the change in size compared to our starting blue triangle?

Well, let's call our original length "x". Whatever it is, we end up getting a new triangle layered on top, with a size of 2x + 3x (a + bi in general). And from Pythagoras (I love that gentleman) the "real" distance is

$\displaystyle{\sqrt{(ax)^2 + (bx)^2} = \sqrt{x^2(a^2 + b^2)} = x \cdot \sqrt{a^2 + b^2}}$

That is, we take our original distance (x) and scale it by the size of the new triangle (size of a + bi).

If the new triangle is size 1 ($a^2 + b^2 = 1$) then the distance won't change!

A Few Thoughts

I don't hate rigorous proofs -- I hate pretending they're helpful when they're not. Proofs have two goals:

Show that a result is true. This is for mathematicians presenting results -- students rarely question the validity of facts in math class.
Show why a result is true.

Real, satisfying insight comes from playing with analogies and examples -- not reading distilled, minimalist proofs (especially those which appeal to the sine/cosine addition formulas!).

Polya said it well: “When you have satisfied yourself that the theorem is true, you start proving it."

Happy math.