If the exponential function $e^x$ is water, the hyperbolic functions ($\cosh$ and $\sinh$) are hydrogen and oxygen. They're the technical, rarely-discussed parts that combine into a famous whole.
Admittedly, the hyperbolic functions were tucked into a dark part of my attic. They were defined with strained motivations ("Need yet another way to build a hyperbola?") then crammed into tables of integrals, soon to be forgotten. I couldn't think with them.
After much struggle, I found their purpose:
What are the hyperbolic functions ($\cosh$ and $\sinh$)? The even/odd parts of the exponential function ($e^x$) that, funny enough, can build a hyperbola.
Why are parts of the exponential called hyperbolic? That's the modern name. These functions are so darn good at making hyperbolas that they're typecast for that role. (Similarly, sine isn't just about circles, and we shouldn't name it "circular sine"!)
Why are hyperbolic functions useful? A better framing is: Why are parts of $e^x$ useful? We now have "mini logarithms" and "mini exponentials", with partial versions of $e$'s famous properties.
I can handle it: how do hyperbolas connect to exponentials? Hyperbolas come from inversions ($xy = 1$ or $y = \frac{1}{x}$). The area under an inversion grows logarithmically, and the corresponding coordinates grow exponentially. If we rotate the hyperbola, we rotate the formula to $(x-y)(x+y) = x^2 - y^2 = 1$. The area/coordinates now follow modified logarithms/exponentials: the hyperbolic functions.
Actually, I couldn't handle it. That's ok. We'll build up to it. These functions took many years to be discovered, and their behavior is hardly obvious.
This post is fairly technical: we're studying hydrogen, not water. If hyperbolic functions appear in class, you don't have much choice, and may as well get an intuition. If you're studying for fun, don't sweat the details, that's what calculus students are for.
As a prerequisite, have these insights in mind:
- $e^x$ is the process of continuous, 100% growth
- natural log is the time for $e^x$ to grow to a given value
Let's dive in.
Contents
Part 1: Exponential Viewpoint
Background: Odd/Even Functions
Chemical compounds can be separated into constituent atoms; math objects are similar.
The number 13 can be split into an even part (12) and odd part (1). They combine to the whole: 13 = 12 + 1.
This even/odd split works for functions, too:
![]()
Functions are tricky to separate because they have multiple values. The separation we look for is between the future values ($x > 0$) and the past ones ($x < 0$).
To see what the future and past have in common, take their average:
![]()
To see how the future and past differ, average their gap:
![]()
Can we combine these parts to get the original?
$f_\text{even}(x) + f_\text{odd}(x) = \frac{f(x) + f(-x)}{2} + \frac{f(x) - f(-x)}{2} = \frac{f(x) + f(-x) + f(x) - f(-x)}{2} = \frac{2f(x)}{2} = f(x)$
Neat trick. We can split any pattern into its even and odd parts.
Taylor series
The Taylor Series (Math DNA) expresses a function as a polynomial:
![]()
The even exponents ($x^0, x^2, ...$) are symmetric in the past and future (for example: $x^2 = (-x)^2$), and the odd exponents are anti-symmetric ($x^3 = - (-x)^3$).
We can quickly extract the even/odd parts by separating the function's Taylor series into even/odd exponents:
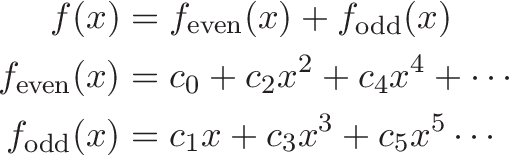
Even and Odd Exponentials
Ok, we have our trick. Why not try to split up the famous exponential function?
![\begin{align*}
e^x_{\text{even}} &= \text{avg}[e^x, e^{-x}] = \frac{e^x + e^{-x}}{2} = \cosh(x) \\
e^x_\text{odd} &= \text{avg}[e^x, -e^{-x}] = \frac{e^x - e^{-x}}{2} = \sinh(x) \\
e^x &= e^x_{\text{even}} + e^x_{\text{odd}} = \cosh(x) + \sinh(x)
\end{align*}](https://betterexplained.com/wp-content/plugins/wp-latexrender/pictures/57c4683189f9e74ddebed533a6931e7b.png)
Instead of the awkward $e^x_{\text{even}}$ and $e^x_{\text{odd}}$, we call the even part $\cosh$ (hyperbolic cosine) and the odd part $\sinh$ (hyperbolic sine). (The pronunciation varies.)
Now, why the adjective "hyperbolic"? Euler used the quantity $(e^{x} + e^{-x})$ without giving it a special name. Lambert later called them "transcendental logarithmic functions", and even later the ability to build hyperbolas was seen. That use case has stuck.
Call me old-fashioned, but parts of $e^x$ are interesting for that reason alone. I don't need a hyperbola to justify their utility.
Part 2: What do hyperbolic functions look like?
Let's graph $\cosh$ and $\sinh$ with their parent:
- $e^x$ is our standard exponential, with Taylor series: $e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + ...$
- $\cosh(x)$ is a gentle bowl. It's roughly parabolic, then expands exponentially, with Taylor series: $\cosh(x) = 1 + \frac{x^2}{2!} + \frac{x^4}{4!} + ...$
- $\sinh(x)$ looks linear at first, then grows exponentially also: $\sinh(x) = x + \frac{x^3}{3!}...$
Now for a usually-confusing question: What does the parameter $x$ in $\cosh(x)$ really mean?
It's nothing special! It's the same $x$ we feed to any exponential, usually the time to grow: $e^x = e^{rt} = e^{100\% t}$.
We can see the hyperbolic trig functions as:
- $\cosh(x)$: What is the even part of $e^x$ after $x$ units of time?
- $\sinh(x)$: What is the odd part of $e^x$ after $x$ units of time?
A few gut checks:
- What's $\cosh(0)$? At $x=0$ (aka $\text{time} = 0$), we haven't moved from 1.0 (the exponential starting point). The average is 1, and there's no separation, so $\sinh(0) = 0$.
- As time goes on, the future grows and the past ($e^{-x}$) vanishes. The average value becomes $\frac{e^x + 0}{2}$, and the average difference becomes $\frac{e^x - 0}{2}$. For large $x$, we'd expect $\cosh(x) \sim \sinh(x) \sim 0.5 e^x$.
Now, how about the inverse hyperbolic functions like $\text{acosh}$ (also called $\text{arccosh}$ or $\text{arcosh}$)? "Inverse hyperbolic cosine" sounds scary, but think of it like this:
$\ln(a)$: How long until $e^x$ reaches value $a$?
$\text{acosh(a)}$: How long until the even part of $e^x$ reaches $a$? This must take longer than $\ln(x)$, since we're only using the even powers in our exponential growth Taylor series.
- $\text{asinh(a)}$: How long until the odd part of $e^x$ reaches $a$? Similarly, this must require more time $\ln(x)$.
In the graphs above, $\text{acosh}$ and $\text{asinh}$ require more time (i.e., are above) the natural log.
Intuitively, I see the various hyperbolic functions as modified exponentials and logarithms:
- $\cosh$ and $\sinh$ are partial/delayed exponential curves (with new behavior near zero, where the past still has influence).
- $\text{acosh}$ and $\text{asinh}$ are slower versions of the natural log. It takes $\ln(3) = 1.09$ units for $e^x$ to grow from 1 to 3, but it takes $\text{acosh}(3) = 1.76$ units for just the even part of $e^x$ to do the same.
Part 3: Applications of the Exponential Interpretation
Since $\cosh$ and $\sinh$ are mini exponentials (those little cherubs!), we'd guess they still have interesting properties.
Function equal to its own second derivative
$e^x$ is the function equal to its own derivative ($f' = f$).
![]()
Ok. And Sine and cosine are functions equal to their own fourth derivatives ($f'''' = f$).
![]()
Repeating after one derivative, repeating after four derivatves... that's a big gap. Anything in-between?
You bet. The hyperbolic functions equal their own second derivative ($f'' = f$):
![]()
![]()
Unlike $\sin$ and $\cos$, there's no awkward negative signs in the cycle, just a toggle:
![]()
Neat. The hyperbolic functions are like "half exponentials" because it takes two derivatives to complete the cycle. This is why they're useful in calculus -- not because we care about the coordinates on a hyperbola!
Understanding Integral Tables
You'll see hyperbolic functions in tables of tricky integrals and derivatives:
Ignore the specifics. Let's see the general pattern without getting lost in the details.
We have our standard relationship:
![]()
Since the hyperbolic functions are variations of the exponentials, we'd expect $\frac{d}{dx}\text{asinh}$ to resemble $\frac{1}{x}$. From the table:
![]()
When $x$ is large, the "$+ 1$" doesn't matter much, and the derivative becomes:
![]()
Ah! The function $\text{asinh}(x)$ behaves like $\ln(x)$, except for small $x$ where the $+1$ term still matters. Without this exponential perspective, I'd have no clue what the derivative of $\text{asinh}$ should resemble. (You want the rate of change of the inverse function that determines the y-coordinate a in a hyperbola? What?)
New descriptions of Sine and Cosine
Remember, we can now split the exponential function whenever we want:
![]()
So, what if we plug in $ix$? We'd get
![]()
But Euler's formula says:
![]()
Whoa. The even/odds parts of each function must be the same, so:
![]()
![]()
If we feed the imaginary axis to our everyday exponential function, we get the trig functions which live on a circle. The rotation is happening via the parameter $ix$, vs. in the function $e^{ix}$. (Instead of rotating the steering wheel, we're rotating the engine, so to speak.)
In sine's case, we have an awkward imaginary term to shuffle around:
![]()
These connections are more useful in complex analysis (still learning...), normally you'd prefer to pass real parameters into functions.
New Trig Identities
A few new identities doesn't hurt. With some quick algebra, we can turn regular trig identities into their hyperbolic versions. Starting with:
![]()
We swap in $\cos(x) = \cosh(ix)$ and $\sin(x) = -i \sinh(ix)$ to get:
![\begin{align*}
\cosh^2(ix) + [-i\sinh(ix)]^2 &= 1 \\
\cosh^2(ix) + i^2\sinh^2(ix) &= 1 \\
\cosh^2(ix) -\sinh^2(ix) &= 1
\end{align*}](https://betterexplained.com/wp-content/plugins/wp-latexrender/pictures/d0e992723f18aae63ab8f60ae6364261.png)
Now, the term $ix$ is just a parameter. To simplify things, just say $z = ix$ and write:
![]()
We can leave out the specific parameter and write:
![]()
This pattern works in general. To convert a regular trig formula to its hyperbolic equivalent (Osborne's Rule), swap:
- $\cos^2 \Rightarrow \cosh^2$
- $\sin^2 \Rightarrow -\sinh^2$ (due to the $i$ when converting $\sin$ into $\sinh$)
Machine Learning Functions
While looking for applications of $\cosh$, I ran across this function, used in Machine Learning:
![]()
A direct interpretation is confusing: "Take the natural log of the x-coordinate in a hyperbola". Huh? What does that represent?
The exponential perspective makes it simpler:
- We don't want to take the natural log of the regular exponential, since $\ln(e^x) = x$. A function like $x$ (or rather, the absolute value $|x|$) is too pointy, and doesn't have a clean derivative at zero.
- However, $\cosh(x)$ only resembles the regular exponential function. Its natural log will only resemble $f(x) = x$. The resulting function $\ln(\cosh(x))$ looks parabolic near zero, and linear as we grow:
How does this work? For small $x$:
- $\cosh(x) \approx 1 + \frac{x^2}{2}$. These are the first few terms of its Taylor series.
- $\ln(1 + x) \approx x$. The time to grow from 1.0 to 1 + .01 at 100% interest is only .01 units (not enough time for compounding)
- Combining the approximations, we get: $\ln(\cosh(x)) \approx \ln(1 + \frac{x^2}{2}) \approx \frac{x^2}{2}$.
As $x$ increases, we approach an offset line:
![]()
Cool! We have a parabola-line hybrid. No need for hyperbolas, we're dealing with variations of the exponential function.
Bonus: Lining Things Up
Maybe we can get $\text{logcosh}$ to turn into the line $y = x$, instead of the offset line $y = x - \ln(2)$. We can add a term to undo the $-\ln(2)$:
![]()
Notes:
- Our new function (purple) still looks like a parabola for small $x$.
- The $x^2$ in the in $e^{-0.1x^2}$ makes the function symmetric.
- Adjusting the constant $0.1$ changes how fast we approach the line $y=x$.
A short while back, I'd have no idea how to make a parabola gently transition into a line. But seeing $\cosh$ as "parabolic short term, exponential long term" gives us a clue: use the natural log to undo the "exponential long term" behavior, giving us "parabolic short term, linear long term".
Hyperbolic Tangent
The hyperbolic tangent is used as a machine learning activation function:
![]()
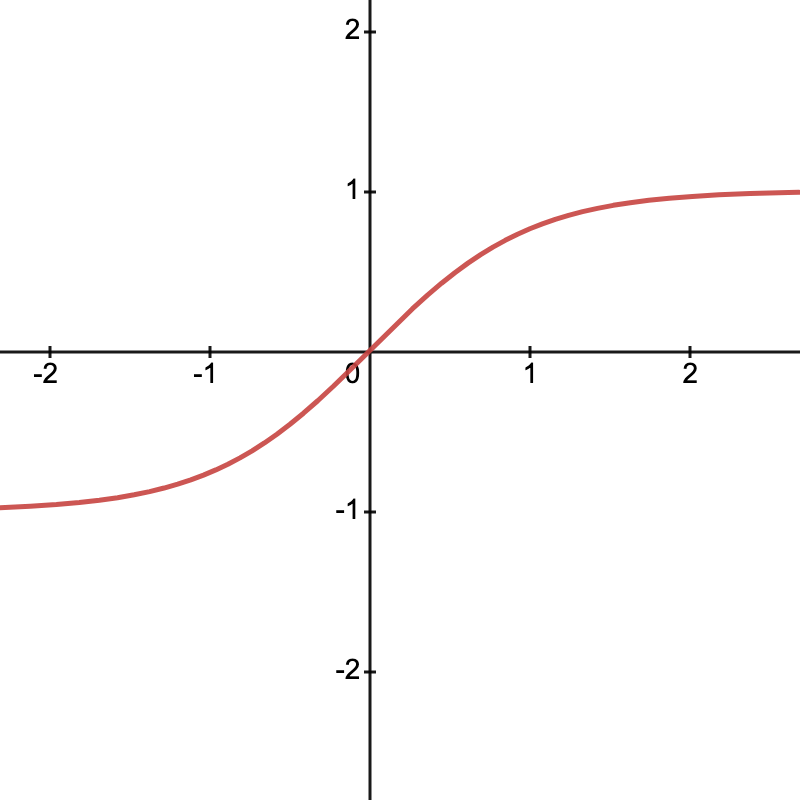
What's its meaning? It's the ratio between the odd and even parts of the exponential function after a given amount of time.
- At $x=0$, the even part dominates (full symmetry between past and future)
- As $x$ grows, the odd part catches up, and the ratio approaches 1 (equal parts symmetry and anti-symmetry)
The function $\tanh$ is nicely centered at 0 and smoothly varies between -1 and 1. As $x$ increases, $\cosh(x) \sim \sinh(x) \sim 0.5e^x$ and $\frac{0.5e^x}{0.5e^x} = 1$.
Part 4: Geometric Viewpoint
Ok. We've gone pretty far without talking about hyperbolas. Why?
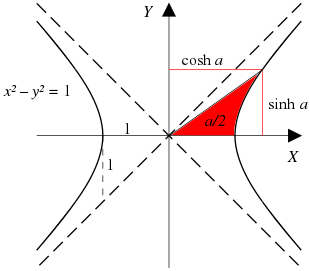
Well, just look at it. They aren't an everyday shape. What's their purpose? Catenaries, orbital mechanics? That's an application but not the reason they exist.
Time to build an intuition.
The Inverse Function Hyperbola (xy=1)
Hyperbolas are built from inverse functions, like $y = \frac{1}{x}$. It's a simple, useful relationship: what's the inverse of $x=2$? $y=1/2$. Multiply them and we undo all scaling: $xy=1$.
A burning math question might be: sure, we have this inverse relationship, but what's the area underneath?
In calculus terms, this is:
![]()
Where
- $\int_1^x$ specifies the boundaries. We start at $x=1$ and go to some upper value for $x$. (We can't start trapping area at $x=0$, since it shoots up to infinity.)
- $\frac{1}{x} dx$ is the area we collect at each x-coordinate as we march along
This integral is hard. Thankfully, one definition of the natural log is:
![]()
so we have a ready-made solution. Starting from $x=1$, what upper x-coordinate will trap 5 units of area? We want to solve:
![]()
Which means
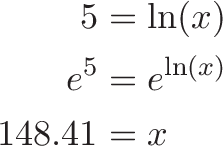
Wow! That's a large coordinate to trap 5 measly units of area.
In general, we have
![]()
And the y-coordinate (inverse) at that position is $y = \frac{1}{x} = \frac{1}{e^{\text{area}}} = e^{-\text{area}}$.
The Rotated Hyperbola
There's multiple ways to make a hyperbolic curve. If we rotate 45 degrees, we get something like this:
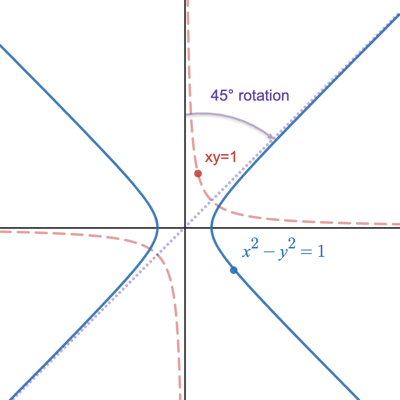
How do we rotate the equation $xy=1$? The standard way is with a rotation matrix, but let's do the rotation with complex numbers.
Let's treat points as complex numbers: $(x, y) \rightarrow x + yi$. A sample point $(a + bi)$ is on the rotated hyperbola if, after undoing the rotation, we see our original $xy = 1$ relationship.
- Candidate point: ($a + bi$)
- 45-degree counterclockwise rotation: $\frac{(1 + i)}{\sqrt{2}}$
![]()
![]()
Ok, we turned our candidate back to its original (pre-rotation) point, which is at
![]()
When does it have our $xy=1$ relationship?
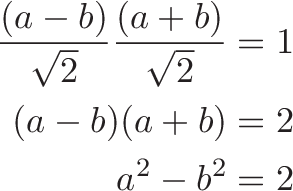
Ok! Our candidate is on the rotated hyperbola if: $a^2 - b^2 = 2$ or $\text{real magnitude}^2 - \text{imaginary magnitude}^2 = 2$. We can express this requirement in $(x, y)$ notation as:
![]()
Almost there. Our original hyperbola ($xy = 1$) contains the point $(1, 1)$, which is a distance of $\sqrt{x^2 + y^2} = \sqrt{1^2 + 1^2} = \sqrt{2}$ from the origin. The constraint equation is really $x^2 - y^2 = r^2$.
If we set the radius to 1, we get a formula for the unit hyperbola:
![]()
Tada! A nice, clean equation, but I also see it as $(x - y)(x + y) = 1$, which hints at the inverse relationship.
Ok. Time for the scary diagram you'll see in most textbooks:
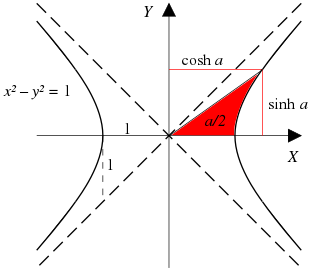
We have our rotated hyperbola, and want to trap $a/2$ units of area in red. (The full $a$ units would include the area under the x-axis. What functions determine the coordinates that trap this area?
The solution turns out to be the even and odd parts of the exponential, $\cosh$ and $\sinh$. There's a 1950's pamphlet "Hyperbolic Functions" by V. G. Shervatot, that goes through the derivation. The key intuition is realizing that hyperbolas (generally speaking) trap area logarithmically, so the necessary coordinates grow exponentially:
- $xy = 1$ hyperbola (trap area under curve)
- $\text{x-coordinate} = e^{\text{area}}$
- $\text{y-coordinate} = \frac{1}{e^{\text{area}}} =e^{-\text{area}} $
- $x^2 - y^2 = 1$ hyperbola (trap $\frac{\text{area}}{2}$ per diagram)
- $\text{x-coordinate} = \frac{e^{\text{area}/2} + e^{-\text{area}/2}}{2} = \cosh(x)$
- $\text{y-coordinate} = \frac{e^{\text{area}/2} - e^{-\text{area}/2}}{2} = \sinh(x)$
In case it needs to be said: it's not obvious that the even/odd parts of the exponential function determine the coordinates that trap area in a rotated hyperbola.
(Aside: Hyperbolas can be defined in terms of distance to fixed points or a conic section, but this gives no intuition for why exponentials are involved.)
The Secant/Tangent hyperbola
One more confusion is why we need new functions to parameterize the hyperbola, when existing trig functions do the trick:
Start with a circle
For any angle $x$, we have coordinates $(x, y)$ = $(\cos(x), \sin(x))$
- If we invert the x coordinate (hey, it's what hyperbolas do), we get $x = \frac{1}{\cos(x)} = \sec(x)$
- If we scale the y coordinate by that same inversion, we get $y = \sin(x) \cdot \frac{1}{\cos(x)} = \tan(x)$
Does this really make a hyperbola? It meets the requirements:
$x^2 - y^2 = 1$ (relationship needed for rotated hyperbola)
$\sec^2(t) - \tan^2(t) = 1$ (rearrangement of the famous $\sec^2(t) = 1 + \tan^2(t)$)
This video shows how the various parameterizations behave (open the calculator):
Our familiar trig functions ($\sec(t), \tan(t))$ trace the same hyperbola as the fancy new $(\cosh(t), \sinh(t))$. They just go a different speed. And the parameter $t$ is just an everyday angle we plug into trig functions.
Although there are multiple parameterizations for the hyperbola, $\cosh$ and $\sinh$ are defined with exponentials and are the analog of $\sin$ and $\cos$ in Euler's Formula. They can wear the Official Hyperbolic Parameterization crown.
Revisiting Inverse Functions
The inverse hyperbolic functions go from coordinates back to area. Let's say I'm on the unit hyperbola, with an x-coordinate of 5. How much area have I trapped? $\text{acosh}(5) = 2.29$.
The inverse functions are sometimes called $\text{arcosh}$ ("area hyperbolic cosine"). This forces us to think about the coordinate-to-area conversion. I prefer to think about exponentials, and use $\text{acosh}$ ("inverse hyperbolic cosine"). Area is one interpretation, don't force me into it.
We can derive the formulas for the inverse functions by solving $x = \cosh(y)$ and $x = \sinh(y)$:
![]()
![]()
As expected, these look like modified logarithms. As $x$ grows, they approach $\ln(x + x) = \ln(2x) = \ln(x) + \ln(2)$, or the natural logarithm with an offset.
Part 5: Applications of the Geometric Interpretation
The Catenary
The main application of the geometric view is that the $\cosh(x)$ is the shape a rope takes when hanging between two fixed points. It's not quite a parabola, it's a catenary curve, with the St. Louis Arch as a famous example. Here's a few more curves (source) that follow $\cosh(x)$:
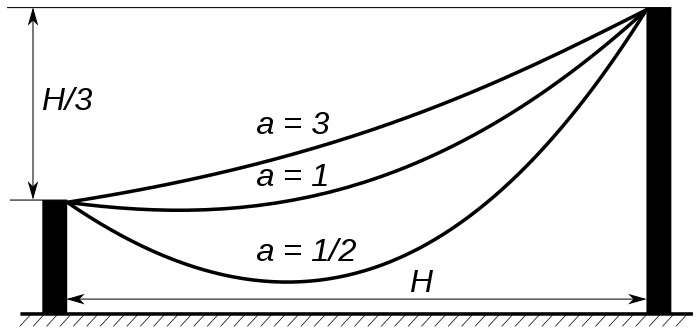
The process to build this curve is fairly subtle:
- First, create a rotated hyperbola with $x^2 - y^2 = 1$
- Instead of using the hyperbola, make a graph of just the x-coordinate.
- This graph of just the x-coordinate makes a new curve, which models how the rope hangs
This convoluted process isn't how $\cosh$ was discovered. There's a differential equation that models the forces inside a hanging rope:
![]()
To solve the differential equation, we need the convenient exponential properties of $\cosh$, and wind up with:
![]()
It's cute that $\cosh$ parameterizes a hyperbola, but that interpretation has nothing to do with why it's the solution. I think "the catenary follows the even part of the exponential function" not "the catenary follows the x-coordinate of the hyperbola".
Shape Where Arc Length = Area
The area under the exponential $e^x$ equals the current value (plus a constant). Consider the region from $x=0$ to $x=2$:
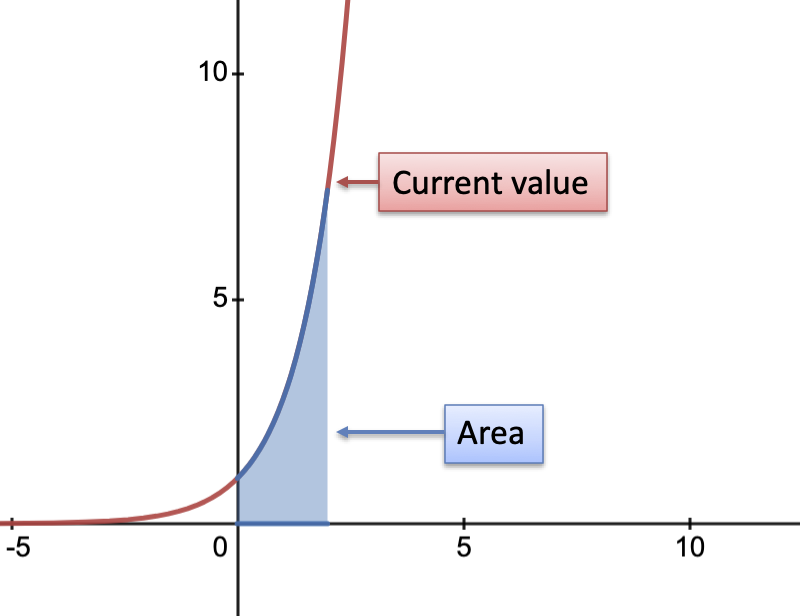
- Area under curve: $\int_0^2 e^x = e^2 - e^0 = 7.389 - 1 = 6.389$
- Current value: $e^2 = 7.389$
- Pattern: $\text{current value} = \text{area under curve} - 1$
A pretty clean connection, right? (Don't forget that $+C$)
Now how about $\cosh$?
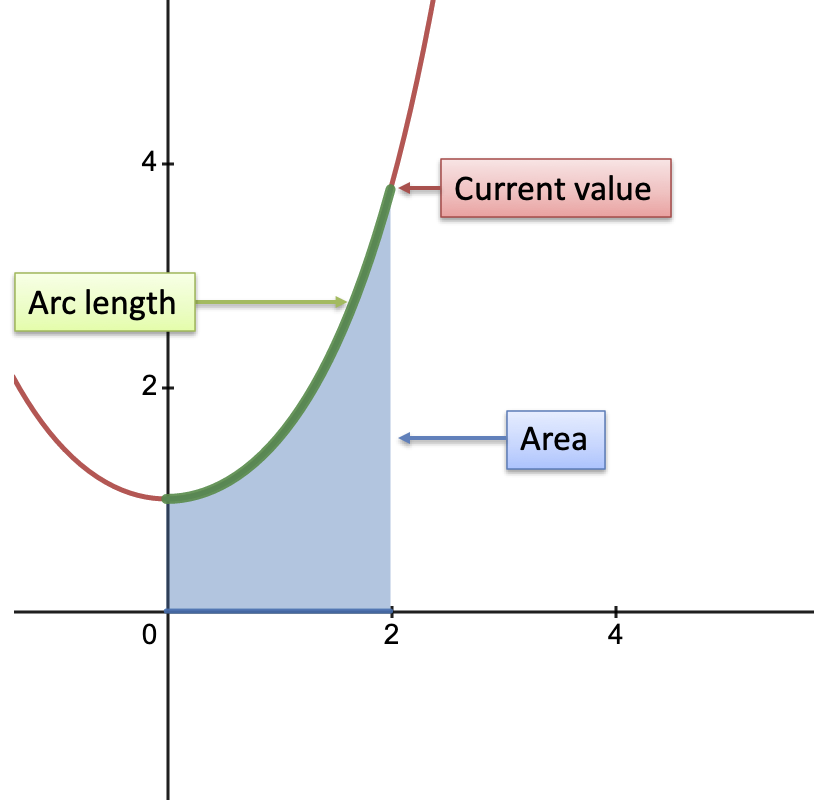
- Current value: $\cosh(x)$
- Area under curve: $\int \cosh(x) = \sinh(x)$
- Arc length of curve: $\int \sqrt{1 + (\cosh'(x))^2} = \int \sqrt{1 + \sinh^2(x)} = \int \cosh(x) = \sinh(x)$
- Pattern: $\text{area under curve} = \text{arc length} = \sqrt{\text{current value}^2 - 1}$
The current value of $\cosh$ can be swapped in using the identity $\sqrt{\cosh^2 - 1} = \sinh$.
For large $x$, the $-1$ is negligible and $\sqrt{\text{current value}^2 - 1} \sim \text{current value}$. So, for large $x$, we get equality between area, arc length, and current value (imagine the green rope hanging down and just touching the x-axis). It's more connected than regular $e^x$, not bad!
(Intuition for another day: Math deals with unitless quantities. $13 \ \text{cm}$ is not directly comparable with $13 \ \text{cm}^2$. Yet in math class, we can solve $x = 1 + x^2$ and nobody cares that constant, linear and squared terms are used in conjunction.)
Hyperbolic Geometry
The shape of the universe may be a hyperbola, and hyperbolic geometry is used in special relativity (beyond my pay grade). If we do live in a giant hyperbola, I, uh, may be forced to recant my "exponentials first" stance.
Summary
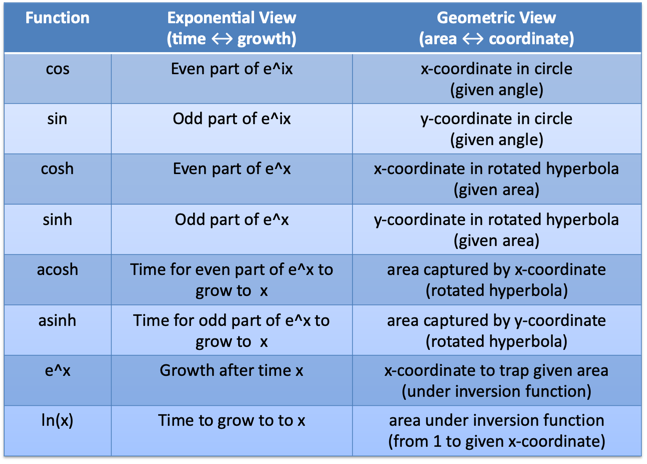
The hyperbolic functions can be seen as exponential functions (relating time and growth) or geometric functions (relating area and coordinates). Hyperbolas, generally speaking, have logarithmic area and exponential coordinates.
It's been a long journey, but these functions don't haunt my attic any more.
Happy math.
References
- Various Hyperbolic Relations
- Enter, Stage Center: The Early Drama of the Hyperbolic Function (pdf)
- Proof of Osborne's Rule
- Rotating the xy=1 hyperbola
- Hyperbolic Functions by V. G. Shervatov
- Geometric derivation of hyperbolic functions
Other Posts In This Series
- A Visual, Intuitive Guide to Imaginary Numbers
- Intuitive Arithmetic With Complex Numbers
- Understanding Why Complex Multiplication Works
- Intuitive Guide to Angles, Degrees and Radians
- Intuitive Understanding Of Euler's Formula
- An Interactive Guide To The Fourier Transform
- Intuitive Guide to Convolution
- Intuitive Understanding of Sine Waves
- An Intuitive Guide to Linear Algebra
- A Programmer's Intuition for Matrix Multiplication
- Imaginary Multiplication vs. Imaginary Exponents
- Intuitive Guide to Hyperbolic Functions