Imaginary Multiplication vs. Imaginary Exponents

Imaginary numbers perform rotations. So what's the difference between $2 i$ and $2^i$?

Imaginary multiplication directly rotates our position
Imaginary exponents rotate the direction of our exponential growth; we compute our position after the sideways growth is complete

I think of imaginary multiplication as turning your map 90 degrees. East becomes North; no matter how long you drove East, now you're going North.

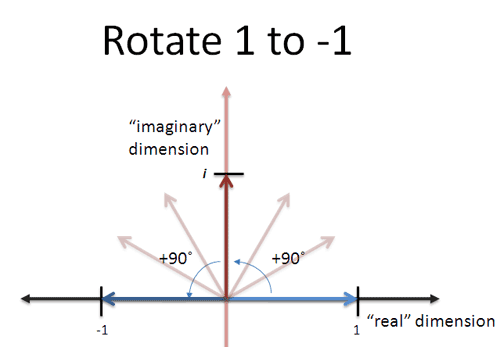
An imaginary exponent is like turning just the steering wheel. Where you will end up? Depends how long you drive!

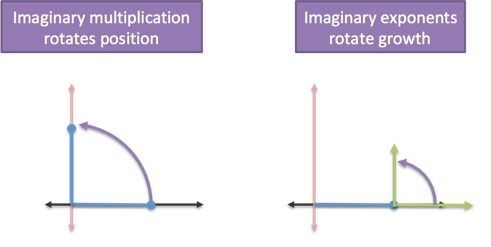
That's the intuition, let's work through the details.

Multiplication World and Exponent World

The math is straightforward when multiplying by $i$. We perform a 90-degree rotation around the origin, so 1 becomes $1i$, 2 becomes $2i$, and so on:

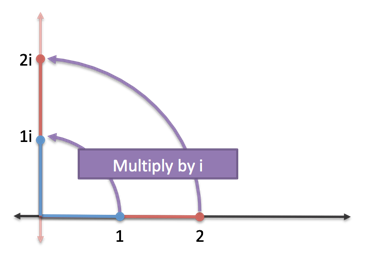
This is Multiplication World, where numbers are plopped on the number line then slid around (added), stretched (multiplied), shrunk (divided), and so on. Rotating a number is new, but not overly strange.

Unfortunately, the Multiplication World perspective isn't great for exponents. If we see exponents as "repeated multiplication" we're stuck when we try to count $i$ times. It's the wrong model.

Nope -- to use $i$ in the exponent, we need to enter Exponent World.

Here, numbers are grown, not simply plopped down on the number line. Every number starts at 1.0, then we run an exponential growth engine at 100% for some period of time:

e^0 = 1.0 (no fuel, you stay the same)
e^1 = 2.71828... (1 unit of fuel, with continuously compounding interest)
e^2 = 7.3189... (2 units of fuel, with continuously compounding interest)

In Exponent World, a familiar number like "2" is just 1.0, grown for .693 seconds at a 100% continuous interest rate. In other words:

$\displaystyle{2 = e^{\ln(2)} = e^{.693 \cdot 100\%}}$

And in general:

$\displaystyle{x = e^{\ln(x) \cdot 100\%}}$

$e^x$ is an rocketship that pushes our numbers ever further from our starting point of 1. At t=3 we're around 20, and at t=10 we're over 20,000.

So, what happens if we drop an imaginary number into the exponent ($e^{1} \rightarrow e^{1i}$)? We keep the same amount of fuel, but rotate our engine sideways:

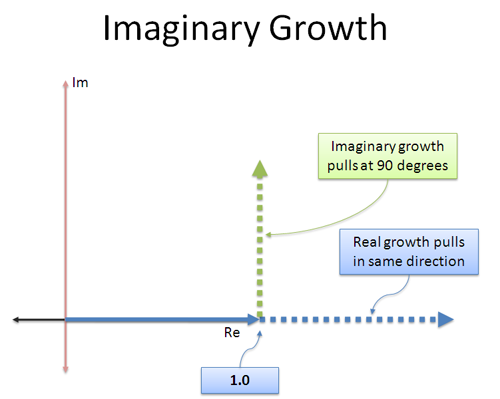
With regular exponential growth, we expect to speed along the real dimension. With our sideways engine, we'll need to compute what will happen.

Euler's Formula gives us the answer: constant force in a perpendicular direction creates an orbit:

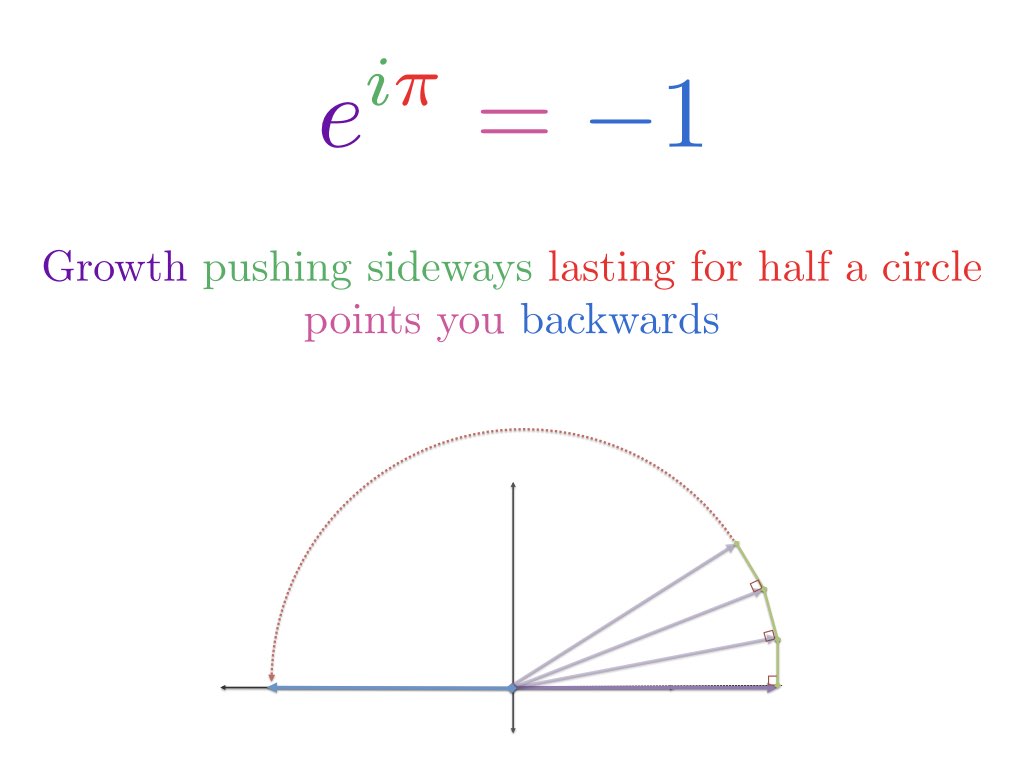
and in general:

A few notes/gotchas:

We always start at 1.0. When seeing $e = 2.718...$, it's tempting to think growth starts from 2.718. But no -- when we write $e^x$ we're still begin the growth process at 1.0 ($e^0 = 1$ implies no change from 1.0).

I try to remember we can swap $e$ for its official definition at any time:

The only starting point we see in the definition is 1.

Every number orbits at a radius of 1.0. In exponent world, every number is grown from 1.0, just with varying amounts of fuel. When we put the engine sideways, the orbits are at 1.0, for varying distances around the circle.
The orbit doesn't get faster. Regular exponential growth has runaway compounding because our changes accumulate in the same direction. With sideways growth, changes don't accumulate (always in a new direction) and we spin at a constant speed. In other words, $e^{10}$ is thousands of times larger than $e^1$, but $e^{10i}$ is only ten times around the circle compared to $e^i$.

Example: Compute 2^i

So, a setup like $2^i$ tells us to use .693 units of fuel in a sideways direction:

$\displaystyle{2^i = e^{\ln(2)i}}$

To get the coordinates for our final position, we see how far ln(2) = .693 units of fuel takes us around the unit circle:

$\displaystyle{2^i = \cos(.693) + i \sin(.693) = .769 + .639i}$

Phew! Working out $2^i$ (rotated exponential growth) is much trickier than $2i$ (a simple rotation).

More trickiness: i^i

Now let's get tricky. What is $i^i$?

Remember, we're in Exponent World, and even $i$ is something we had to grow to! In other words, we start at 1.0 and orbit a quarter of the way around the circle (90 degrees, or $\frac{\pi}{2}$ radians).

$\displaystyle{i = e^{\frac{\pi}{2} i}}$

Whoa. Don't like how $i$ appears in its own exponential definition? It must also bother you that every word in the dictionary is defined by other words.

Coming back to $i^i$, we have two operations.

The bottom $i$ (in the base) is shorthand for running our engine sideways, with $\frac{\pi}{2}$ units of fuel
The top $i$ (in the exponent) says "Nah, spin that engine one more time"
The engine is facing 180 degrees (backwards on the real axis) with $\frac{\pi}{2}$ units of fuel

Ah. The result is

$\displaystyle{i^i = [e^{\frac{\pi}{2} i}]^i = e^{\frac{\pi}{2} i \cdot i} = e^{-\frac{\pi}{2}} = .207...}$

And we end up with a real number. Intuitively, we can roughly predict this because we start at 1.0 and point the engine backwards on the real axis. Once you can mentally estimate the direction $i^i$ goes, in seconds, you've got a sold intuition on imaginary exponents.

Happy math.

Appendix: i * i^i

Just for fun, what about $i \cdot i^i$?

We know that $i^i$ is a purely real number smaller than 1.0. The first $i$ (doing the multiplication) will just rotate us, so now we have a purely imaginary number smaller than $1i$.

Not bad! Work through the exponents, then rotate the final position.

Appendix: Physics Interpretation

From a physics perspective, if $f(x) = e^{ix}$ is our position, then $f'(x)$ is our velocity. Working this out we get:

$\displaystyle{f'(x) = \frac{d}{dx} e^{ix} = i e^{ix} = i \cdot f(x)}$

In other words, our velocity is perpendicular to our position. Taking the derivative of $e^{ix}$ might seem weird, but treat $i$ like any other constant: $\frac{d}{dx} e^{ax} = ae^{ax}$.