Common Definitions of e (Colorized)

Seeing the same math concept from a few perspectives helps build intuition. Seeing that e is my favorite constant (sorry, pi), a while back I put the definitions of e together to visualize their connection:

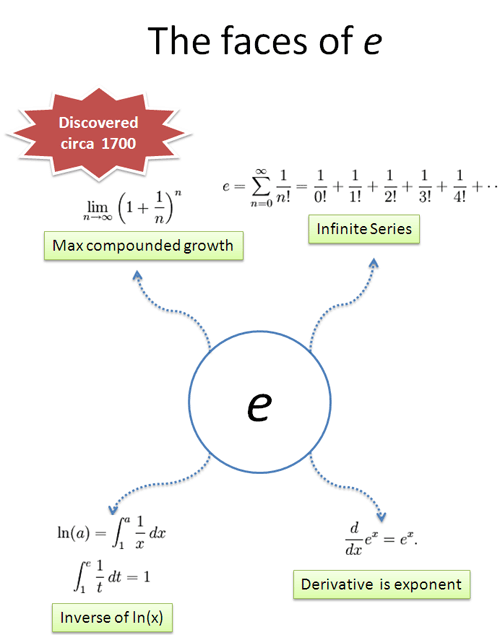
The key intuition: e represents 100% continuous growth.

Today let's revisit each definition with a colorization viewpoint, describing continuous growth from a few different perspectives.

Definition 1: Compound Interest Perfectly

This definition of e was my starting point on understanding the concept. We start with 1 growing to 2 (100% interest), and then compound that growth more and more frequently.

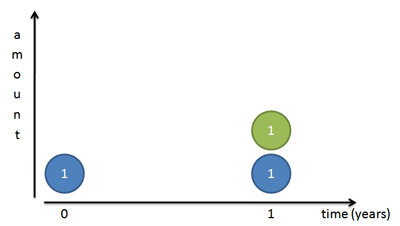
Eventually, we see that 1 grows to 2.71828..., hitting a speed limit of e.

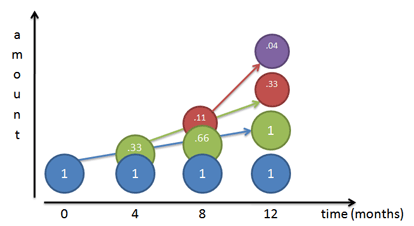
The trick is distinguishing the role of each "1" in the definition. One is the base quantity, one is the interest, and another is the implicit single unit of time we plan to grow for. Math is so abstract that we don't have these separations labeled individually, they are just quantities interacting.

Definition 2: Track Each Interest Contribution

This definition splits up the compounding process into chunks we can see separately. I like to see each component like a "factory" that is earning money. We start with our initial amount, which builds interest. That interest builds its own interest, whcih builds its own interest, and so on (read more).

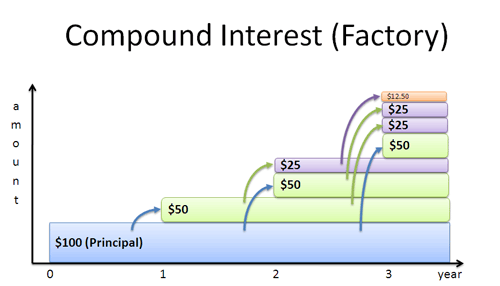
From a calculus perpsective, here's what's happening:

Our initial quantity is 1 (for all time)
This principal earns 100% continuous interest, and after time $x$ has earned $\int 1\, dx = x $. (After 1 unit of time, this is 1)
After time x, that interest ($x$) has earned $\int x \,dx = \frac{1}{2} x^2$. (After 1 unit of time, this is $\frac{1}{2}$)
After time x, that interest ($\frac{1}{2}x^2$) has earned $\int \frac{1}{2} x^2 \,dx = \frac{1}{2}\frac{1}{3}x^3 = \frac{1}{3!}x^3$ (After 1 unit of time, this is $\frac{1}{3!} = \frac{1}{6}$)

And so on. Every instant, the entire chain of interest is growing. When learning calculus, you might have repeatedly tried to integrate $x$ just for fun (whatever gets you going). That game is how we end up with $e$.

Instead of plugging in $x=1$ to compute $e^1$, we can leave $x$ unspecified to handle any amount of time:

$\displaystyle{e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \dots }$

I like seeing how each piece of interest contributes to the whole. Later terms have larger powers, but fight a larger factorial. For very small values of $x$ (like 1%), we can approximate $e^x$ as:

$\displaystyle{e^x \sim 1 + x}$

For example, earning 1% continuous interest for a single year is still around 1.01, because there isn't much growth from compounding. (And yep, $e^.01 = 1.01005$.)

Definition 3: Maintain 100% Continuous Growth

This is the shortest definition, but relies on calculus machinery. In short, we're saying that $e^x$ always changes by exactly the amount that we have.

The derivative ($\frac{d}{dx}$) measures instantaneous change:

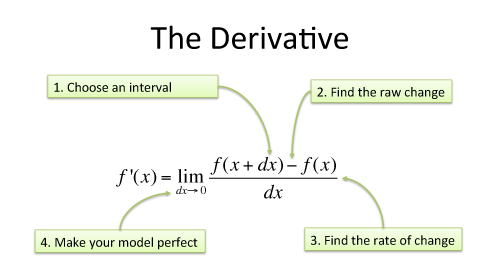
And we say $e^x$ is that input that makes this machine return the original value. (In a similar way, "0" is the input that makes addition return the original; 1.0 is the input that makes multiplication return the original value.)

We can check this works. We saw earlier that $e^x$ is really this equation:

$\displaystyle{e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \dots }$

If you take the derivative each term in the right-hand side we get:

$\displaystyle{e^x = 0 + 1 + \frac{2x}{2!} + \frac{3x^2}{3!} + \dots }$

which simplifies to

$\displaystyle{e^x = 1 + x + \frac{x^2}{2!} + \dots }$

In other words, every term gets "pulled over" to the left, with the constant 1.0 disappearing (it doesn't change). We have our original pattern, therefore $e^x$ is its own derivative. (There's no +C chicanery here, because $\frac{d}{dx} (e^x + C) \neq e^x + C$).

While other functions like $f(x) = x^2$ or $f(x) = \sin(x)$ may momentarily equal their derivative at certain instants, they don't keep it up for all values of $x$. $e^x$ is that Disneyland ride that keeps the magic going forever.

Definition 4: Define e using the natural log

This definition is the most gnarly: instead of talking about e directly, we work backwards.

Define the natural logarithm as the time needed to grow from 1 to $a$ (our desired number), assuming 100% continuous interest. What does that look like?

Let's say we've grown to 4.0. How long to grow to 5.0? Well, assuming 100% interest, we grow 4 units per time period, so it takes us 1/4 of a unit to grow to 5.

And when we're at 5, it'll take us 1/5 of a unit to get to 6.

And so on. The time to grow from to 1 to a is the time from 1 to 2 (1 unit), plus 2 to 3 (1/2 unit), plus 3 to 4 (1/3 unit), until we reach $a$.

(In reality, we need to break time down microscopically, growing from 1, to 1.1, to 1.2, etc. That's what the integral $\int\frac{1}{x}\,dx$ really does.)

Phew! Once we have the notion of "time to grow from 1 to a" defined, we say e is the number that takes 1 unit of time to reach. In other words:

$\displaystyle{\int_1^e \frac{1}{x}dx = 1}$

Here, e is the "base of the natural logarithm".

Trace the similarities

I feel comfortable with an idea when I can hop between definitions and notice similarities. For example, look at the items that show up in each colorization: do you see where "interest" shows up in each definition? The unit quantity? The idea of perfection or infinitely precise change?

It feels great when e becomes a flexible tool on your bat-belt and not an incantation to memorize.

Happy math.