Calculus: Building Intuition for the Derivative

How do you wish the derivative was explained to you? Here's my take.

Psst! The derivative is the heart of calculus, buried inside this definition:

$\displaystyle{ f'(x) =\lim_{dx\to 0} \frac{f(x+dx)-f(x)}{dx}}$

But what does it mean?

Let's say I gave you a magic newspaper that listed the daily stock market changes for the next few years (+1% Monday, -2% Tuesday...). What could you do?

Well, you'd apply the changes one-by-one, plot out future prices, and buy low / sell high to build your empire. You could even stop using the monkeys that pick random stocks for your portfolio.

Like this magic newspaper, the derivative is a crystal ball that explains exactly how a pattern will change. Knowing this, you can plot the past/present/future, find minimums/maximums, and therefore make better decisions. That's pretty interesting, more than the typical "the derivative is the slope of a function" description.

Let's step away from the gnarly equation. Equations exist to convey ideas: understand the idea, not the grammar.

Derivatives create a perfect model of change from an imperfect guess.

This result came over thousands of years of thinking, from Archimedes to Newton. Let's look at the analogies behind it.

We all live in a shiny continuum

Infinity is a constant source of paradoxes ("headaches"):

A line is made up of points? Sure.
So there's an infinite number of points on a line? Yep.
How do you cross a room when there's an infinite number of points to visit? (Gee, thanks Zeno).

And yet, we move. My intuition is to fight infinity with infinity. Sure, there's infinity points between 0 and 1. But I move two infinities of points per second (somehow!) and I cross the gap in half a second.

Distance has infinite points, motion is possible, therefore motion is in terms of "infinities of points per second".

Instead of thinking of differences ("How far to the next point?") we can compare rates ("How fast are you moving through this continuum?").

It's strange, but you can see 10/5 as "I need to travel 10 'infinities' in 5 segments of time. To do this, I travel 2 'infinities' for each unit of time".

Analogy: See division as a rate of motion through a continuum of points

What's after zero?

Another brain-buster: What number comes after zero? .01? .0001?

Hrm. Anything you can name, I can name smaller (I'll just halve your number... nyah!).

Even though we can't calculate the number after zero, it must be there, right? Like demons of yore, it's the "number that cannot be written, lest ye be smitten".

Call the gap to the next number $dx$. I don't know exactly how big it is, but it's there!

Analogy: dx is a "jump" to the next number in the continuum.

Measurements depend on the instrument

The derivative predicts change. Ok, how do we measure speed (change in distance)?

Officer: Do you know how fast you were going?

Driver: I have no idea.

Officer: 95 miles per hour.

Driver: But I haven't been driving for an hour!

We clearly don't need a "full hour" to measure your speed. We can take a before-and-after measurement (over 1 second, let's say) and get your instantaneous speed. If you moved 140 feet in one second, you're going ~95mph. Simple, right?

Not exactly. Imagine a video camera pointed at Clark Kent (Superman's alter-ego). The camera records 24 pictures/sec (40ms per photo) and Clark seems still. On a second-by-second basis, he's not moving, and his speed is 0mph.

Wrong again! Between each photo, within that 40ms, Clark changes to Superman, solves crimes, and returns to his chair for a nice photo. We measured 0mph but he's really moving -- he goes too fast for our instruments!

Analogy: Like a camera watching Superman, the speed we measure depends on the instrument!

Running the Treadmill

We're nearing the chewy, slightly tangy center of the derivative. We need before-and-after measurements to detect change, but our measurements could be flawed.

Imagine a shirtless Santa on a treadmill (go on, I'll wait). We're going to measure his heart rate in a stress test: we attach dozens of heavy, cold electrodes and get him jogging.

Santa huffs, he puffs, and his heart rate shoots to 190 beats per minute. That must be his "under stress" heart rate, correct?

Nope. See, the very presence of stern scientists and cold electrodes increased his heart rate! We measured 190bpm, but who knows what we'd see if the electrodes weren't there! Of course, if the electrodes weren't there, we wouldn't have a measurement.

What to do? Well, look at the system:

measurement = actual amount + measurement effect

Ah. After lots of studies, we may find "Oh, each electrode adds 10bpm to the heartrate". We make the measurement (imperfect guess of 190) and remove the effect of electrodes ("perfect estimate").

Analogy: Remove the "electrode effect" after making your measurement

By the way, the "electrode effect" shows up everywhere. Research studies have the Hawthorne Effect where people change their behavior because they are being studied. Gee, it seems everyone we scrutinize sticks to their diet!

Understanding the derivative

Armed with these insights, we can see how the derivative models change:

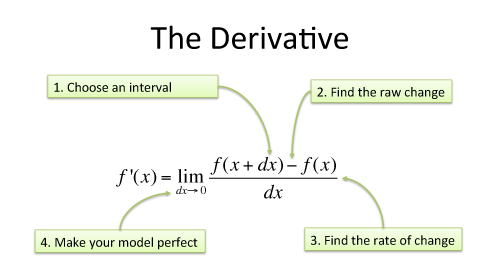
Start with some system to study, $f(x)$:

Change by the smallest amount possible ($dx$)
Get the before-and-after difference: $f(x + dx) - f(x)$
We don't know exactly how small $dx$ is, and we don't care: get the rate of motion through the continuum: $[f(x + dx) - f(x)] / dx$
This rate, however small, has some error (our cameras are too slow!). Predict what happens if the measurement were perfect, if $dx$ wasn't there.

The magic's in the final step: how do we remove the electrodes? We have two approaches:

Limits: what happens when $dx$ shrinks to nothingness, beyond any error margin?
Infinitesimals: What if $dx$ is a tiny number, undetectable in our number system?

Both are ways to formalize the notion of "How do we throw away $dx$ when it's not needed?".

My pet peeve: Limits are a modern formalism, they didn't exist in Newton's time. They help make $dx$ disappear "cleanly". But teaching them before the derivative is like showing a steering wheel without a car! It's a tool to help the derivative work, not something to be studied in a vacuum.

An Example: f(x) = x^2

Let's shake loose the cobwebs with an example. How does the function $f(x) = x^2$ change as we move through the continuum?

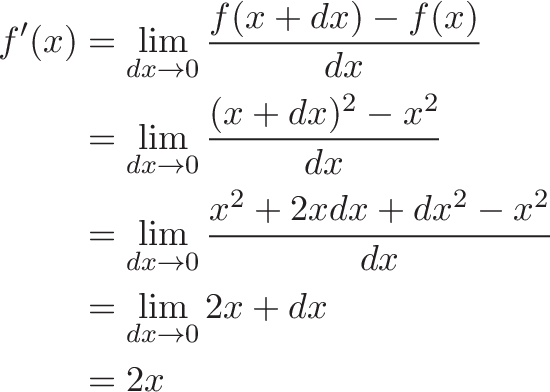
$\begin{aligned} f'(x) &= \lim_{dx\to 0} \frac{f(x+dx)-f(x)}{dx} \\ &= \lim_{dx\to 0} \frac{(x+dx)^2-x^2}{dx} \\ &= \lim_{dx\to 0} \frac{x^2 + 2xdx + dx^2 - x^2}{dx} \\ &= \lim_{dx\to 0} 2x + dx \\ &= 2x \end{aligned}$

Note the difference in the last 2 equations:

One has the error built in ($dx$)
The other has the "true" change, where $dx = 0$ (we assume our measurements have no effect on the outcome)

Time for real numbers. Here's the values for $f(x) = x^2$, with intervals of $dx = 1$:

1, 4, 9, 16, 25, 36, 49, 64...

The absolute change between each result is:

1, 3, 5, 7, 9, 11, 13, 15...

(Here, the absolute change is the "speed" between each step, where the interval is 1)

Consider the jump from $x=2$ to $x=3$ ($3^2 - 2^2 = 5$). What is "5" made of?

Measured rate = Actual Rate + Error
$5 = 2x + dx$
$5 = 2(2) + 1$

Sure, we measured a "5 units moved per second" because we went from 4 to 9 in one interval. But our instruments trick us! 4 units of speed came from the real change, and 1 unit was due to shoddy instruments (1.0 is a large jump, no?).

If we restrict ourselves to integers, 5 is the perfect speed measurement from 4 to 9. There's no "error" in assuming $dx = 1$ because that's the true interval between neighboring points.

But in the real world, measurements every 1.0 seconds is too slow. What if our $dx$ was 0.1? What speed would we measure at $x=2$?

Well, we examine the change from $x=2$ to $x=2.1$:

$2.1^2 - 2^2 = 0.41$

Remember, 0.41 is what we changed in an interval of 0.1. Our speed-per-unit is 0.41 / .1 = 4.1. And again we have:

Measured rate = Actual Rate + Error
$4.1 = 2x + dx$

Interesting. With $dx=0.1$, the measured and actual rates are close (4.1 to 4, 2.5% error). When $dx=1$, the rates are pretty different (5 to 4, 25% error).

Following the pattern, we see that throwing out the electrodes (letting $dx=0$) reveals the true rate of $2x$.

In plain English: We analyzed how $f(x) = x^2$ changes, found an "imperfect" measurement of $2x + dx$, and deduced a "perfect" model of change as $2x$.

The derivative as "continuous division"

I see the integral as better multiplication, where you can apply a changing quantity to another.

The derivative is "better division", where you get the speed through the continuum at every instant. Something like 10/5 = 2 says "you have a constant speed of 2 through the continuum".

When your speed changes as you go, you need to describe your speed at each instant. That's the derivative.

If you apply this changing speed to each instant (take the integral of the derivative), you recreate the original behavior, just like applying the daily stock market changes to recreate the full price history. But this is a big topic for another day.

Gotcha: The Many meanings of "Derivative"

You'll see "derivative" in many contexts:

"The derivative of $x^2$ is $2x$" means "At every point, we are changing by a speed of $2x$ (twice the current x-position)". (General formula for change)
"The derivative is 44" means "At our current location, our rate of change is 44." When $f(x) = x^2$, at $x=22$ we're changing at 44 (Specific rate of change).
"The derivative is $dx$" may refer to the tiny, hypothetical jump to the next position. Technically, $dx$ is the "differential" but the terms get mixed up. Sometimes people will say "derivative of $x$" and mean $dx$.

Gotcha: Our models may not be perfect

We found the "perfect" model by making a measurement and improving it. Sometimes, this isn't good enough -- we're predicting what would happen if $dx$ wasn't there, but added $dx$ to get our initial guess!

Some ill-behaved functions defy the prediction: there's a difference between removing $dx$ with the limit and what actually happens at that instant. These are called "discontinuous" functions, which is essentially "cannot be modeled with limits". As you can guess, the derivative doesn't work on them because we can't actually predict their behavior.

Discontinuous functions are rare in practice, and often exist as "Gotcha!" test questions ("Oh, you tried to take the derivative of a discontinuous function, you fail"). Realize the theoretical limitation of derivatives, and then realize their practical use in measuring every natural phenomena. Nearly every function you'll see (sine, cosine, e, polynomials, etc.) is continuous.

Gotcha: Integration doesn't really exist

The relationship between derivatives, integrals and anti-derivatives is nuanced (and I got it wrong originally). Here's a metaphor. Start with a plate, your function to examine:

Differentiation is breaking the plate into shards. There is a specific procedure: take a difference, find a rate of change, then assume $dx$ isn't there.
Integration is weighing the shards: your original function was "this" big. There's a procedure, cumulative addition, but it doesn't tell you what the plate looked like.
Anti-differentiation is figuring out the original shape of the plate from the pile of shards.

There's no algorithm to find the anti-derivative; we have to guess. We make a lookup table with a bunch of known derivatives (original plate => pile of shards) and look at our existing pile to see if it's similar. "Let's find the integral of $10x$. Well, it looks like $2x$ is the derivative of $x^2$. So... scribble scribble... 10x is the derivative of $5x^2$.".

Finding derivatives is mechanics; finding anti-derivatives is an art. Sometimes we get stuck: we take the changes, apply them piece by piece, and mechanically reconstruct a pattern. It might not be the "real" original plate, but is good enough to work with.

Another subtlety: aren't the integral and anti-derivative the same? (That's what I originally thought)

Yes, but this isn't obvious: it's the fundamental theorem of calculus! (It's like saying "Aren't $a^2 + b^2$ and $c^2$ the same? Yes, but this isn't obvious: it's the Pythagorean theorem!"). Thanks to Joshua Zucker for helping sort me out.

Reading math

Math is a language, and I want to "read" calculus (not "recite" calculus, i.e. like we can recite medieval German hymns). I need the message behind the definitions.

My biggest aha! was realizing the transient role of $dx$: it makes a measurement, and is removed to make a perfect model. Limits/infinitesimals are a formalism, we can't get caught up in them. Newton seemed to do ok without them.

Armed with these analogies, other math questions become interesting:

How do we measure different sizes of infinity? (In some sense they're all "infinite", in other senses the range (0,1) is smaller than (0,2))
What are the real rules about making $dx$ "go away"? (How do infinitesimals and limits really work?)
How do we describe numbers without writing them down? "The next number after 0" is the beginnings of analysis (which I want to learn).

The fundamentals are interesting when you see why they exist. Happy math.