This is a realistic learning plan for Calculus based on the ADEPT method.
I have a few minutes for Calculus, what can I learn?
1 minute: The Big Aha!
Level 1: Appreciation
Calculus is the art of splitting patterns apart (X-rays, derivatives) and gluing patterns together (Time-lapses, integrals). Sometimes we can cleverly re-arrange the pattern to find a new insight.
A circle can be split into rings:
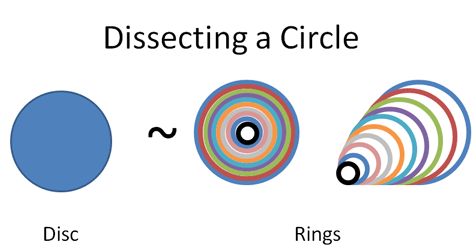
And the rings turned into a triangle:
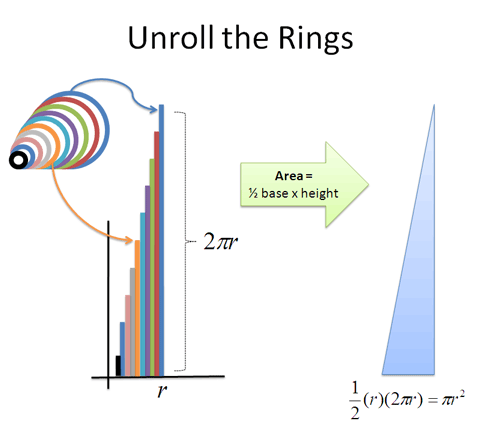
Wow! We found the circle's area in a simpler way. Welcome to Calculus.
Checkpoint:
- Do you want to learn more more?
+20 minutes: Intuitive Appreciation
Level 2: Natural Description
Read:
- Lesson 1 - Use X-Ray and Time-Lapse Vision
- Lesson 2 - Practice Your X-Ray and Time-Lapse Vision
- Lesson 3 - Expanding Our Intuition
Checkpoint: Describe, in your own words:
- What Calculus does
- X-Ray Vision
- Time-lapse Vision
- The tradeoffs when splitting a circle into rings, wedges, or boards
- How to build a 3d shape from 2d parts
+20 minutes: Technical Description
Level 3: Symbolic Description
Read:
Checkpoint: Describe, in your own words:
- Integral
- Derivative
- Integrand (a single step)
- Bounds of integration
Skills:
- Describe a Calculus action (splitting a circle into rings) using the official language
- Enter the official language into Wolfram Alpha to solve the problem
+30 minutes: Theory I
Level 4: Basic Theory
Read:
- Lesson 6 - Improving Arithmetic And Algebra
- Lesson 7 - Seeing How Lines Work
- Lesson 8 - Playing With Squares
Checkpoint: Describe, in your own words:
- How integrals/derivatives relate to multiplication/division
Skills:
- Find the derivative/integral of a line
- Find the derivative/integral of a constant
- Find the derivative/integral of a square
- Recognize the common notations for the derivative
- Estimate the change in f(x) = x2 using a step of size dx
+1 hour: Theory II
Read:
- Lesson 9 - Working With Infinity
- Lesson 10 - The Theory Of Derivatives
- Lesson 11 - The Fundamental Theorem Of Calculus (FTOC)
- Lesson 12 - The Basic Arithmetic Of Calculus
- Lesson 13 - Finding Patterns In The Rules
- Lesson 14 - The Fancy Arithmetic Of Calculus
Checkpoint: Describe, in your own words:
- How an infinite process can have a finite result
- How a process with limited precision can point to a perfect result
- The formal definition of the derivative
- Estimate the change in f(x) = x2 using a step of size dx, and let dx go to zero. Verify the limit using Wolfram Alpha.
- The Fundamental Theorem of Calculus (FTOC)
Derive and put into your own words:
- The addition rule: (f + g)' = ?
- The product rule: (f · g)' = ?
- The inverse rule: (frac(1)(x))' = ?
- The power rule: (xn)' = ?
- The quotient rule: (frac(f)(g))' = ?
- Solve frac(d)(dx) 3x5 on your own and verify with Wolfram Alpha
- Solve int 2x2 on your own and verify with Wolfram Alpha
+1 hour: Basic Problem Solving
Level 5: Basic Performance
Read:
Checkpoint: Describe how to turn the circumference of a circle into the area of a circle:
- Explain your plan in plain English
- Explain your plan using the official math notation
- Apply the rules of Calculus to your equation and calculate the result
- Verify the result using Wolfram Alpha
- Repeat the steps above, turning the area of a circle into the volume of a sphere
- Repeat the steps above, turning the volume of a sphere into the surface area of a sphere
Buy on Amazon
+12 weeks: I need to pass a course!
Level 5: Advanced Performance
Gotcha. The best use of time is still spending a few hours on the above goals, to build a solid intuition. Then, begin your Calculus course, such as:
Elementary Calculus: An Infinitesimal Approach by Jerome Keisler (2002). This book is based on infinitesimals (an alternative to limits, which I like) and has plenty of practice problems. Available in print or free online.
Calculus Made Easy by Silvanus Thompson (1914). This book follows the traditional limit approach, and is written in a down-to-earth style. Available on Project Gutenberg and print.
MIT 1801: Single Variable Calculus. Includes video lectures, assignments, exams, and solutions. Available free online.
As you go through the traditional course, keep this in mind:
Review the intuitive definition. Rephrase technical definitions in terms that make sense to you.
It's completely fine to use online tools for help. When stuck, get a hint, fix your mistakes, and try solving a new problem on your own.
Relate graphs back to shapes. Most courses emphasize graphs and slopes; convert the concepts to shapes to help visualize them.
Skip limits if you get stuck. Limits (and infinitesimals) were invented after the majority of Calculus. If you struggle, move on and return later.
