Chapter 8 Playing With Squares
We’ve seen how lines behave: they change the same amount with each step. Now let’s try a more complex function like \( f(x) = x^2 \). It’s a more detailed scenario, so let’s visualize it.
Imagine you’re building a square garden, to plant veggies and enjoy cucumbers in a few months. You’re not sure how large to make it. Too small, and there’s not enough food, but too large, and you’ll draw the attention of the veggie mafia.
Your plan is to build the garden incrementally, foot-by-foot, until it looks right. Let’s say you start from scratch and build up to a 10 \( \times \) 10 plot:

To the untrained eye, you have single a 10 \( \times \) 10 garden, which uses 40 feet of perimeter fencing (10 \( \times \) 4) and 100 square feet of topsoil (10 \( \times \) 10). (Assume topsoil is sold by the square foot, with a standard thickness.)
8.1 Bring On The Calculus
That’s it? The analysis just figures out the current perimeter and square footage? No way.
By now, you should be clamoring to use X-Ray and Time-Lapse vision to see what’s happening under the hood. Why settle for a static description when we can know the step-by-step description too?
We can analyze the behavior of the perimeter pretty easily:
The change in perimeter (\( \frac{dP}{dx} \)) is a constant 4. For every 1-foot increase in \( x \), we have a 4-foot jump in the perimeter.
We can visualize this process. As the square grows, we push out the existing sides and add 4 corner pieces (in yellow):

The visual is helpful, but not required. After our exposure to how lines behave, we can glance at an equation like \( p = 4x \) and realize that \( p \) jumps by 4 whenever \( x \) jumps by 1.
8.2 Changing Area
Now, how does area change? Since squares are fairly new, let’s X-Ray the shape as it grows:
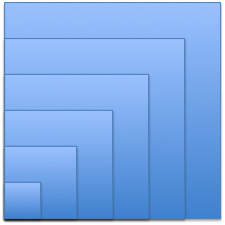
We can write out the size of each jump, like so:
| \( x \) | \( x^2 \) | Jump to next square |
| 0 | 0 | 1 (\( 1^2 - 0^2 = 1 \)) |
| 1 | 1 | 3 (\( 2^2 - 1^2 = 3 \)) |
| 2 | 4 | 5 (\( 3^2 - 2^2 = 5 \)) |
| 3 | 9 | 7 |
| 4 | 16 | 9 |
| 5 | 25 | 11 |
| 6 | 36 | 13 |
| 7 | 49 | 15 |
Now that’s interesting. The gap from \( 0^2 \) to \( 1^2 \) is \( 1 \). The gap from \( 1^2 \) to \( 2^2 \) is \( 3 \). The gap from \( 2^2 \) to \( 3^2 \) is \( 5 \). And so on – the odd numbers are sandwiched between the squares! What’s going on?
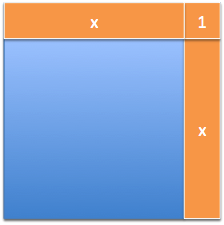
Ah! Growing to the next-sized square means we’ve added a horizontal and vertical strip (\( x + x \)) and a corner piece (1). If we currently have a square with side \( x \), the jump to the next square is \( 2x + 1 \). (If we have a \( 5 \times 5 \) square, getting to a \( 6 \times 6 \) will be a jump of \( 2(5) + 1 = 11 \). And yep, \( 36 - 25 = 11 \).)
Again, the visualization was nice, but it took effort. Algebra can simplify the process.
In this setup, if we set our change to \( dx = 1 \), we get
Algebra predicts the size of the slices without a hitch.
8.3 Integrals and the Veggie Mafia
The derivative takes a shape, a direction to cut, and finds a pattern of slices. Can we work backwards, from the slices to the shape? Let’s see.
Suppose the veggie mafia spies on your topsoil and fencing orders. They can’t see your garden directly, but what can they deduce from your purchases?
Let’s say they observe a constant amount of fencing being delivered (4, 4, 4, 4…) but increasing orders of topsoil (1, 3, 5, 7, 9, 11…). What can they work out?
A low-level goon might just add up the total amount accumulated (the definite integral): “Heya boss, looks like they’ve built some garden with a total perimeter of 40-feet, and total area of 100 square feet.”
But that’s not good enough! The goon doesn’t know the shape you’re trying to build. He saw order after order go by without noticing the deeper pattern.
The crime boss is different: he wants the indefinite integral, the pattern you are following. He’s savvy enough to track the pattern as the orders come in: “The area is increasing 1, 3, 5, 7… that’s following a \( 2x + 1 \) area increase pattern!”
Now, there are likely many shapes that could grow their area by \( 2x + 1 \). But, combined with a constant perimeter increase of 4, he suspects you’re making a square garden after a few deliveries.
How does the godfather do it? Again, by working backwards. He’s split apart enough shapes (triangles, squares, rectangles, etc.) that he has a large table of before-and-afters, just like the antiques dealer.
When he sees a change of \( 2x + 1 \), a square (\( x^2 \)) is a strong candidate. Another option might be a right triangle with sides \( x \) and \( 2x \). Its area equation is \( \frac{1}{2} x \cdot 2x = x^2 \), so the area would change the same as a square.
And when he sees a perimeter change of a steady 4, he knows the perimeter must be \( 4x \). Ah! There aren’t too many shapes with both properties: a square is his guess. (With enough practice, you start to recognize common patterns; tools like Wolfram Alpha can help.)
Now suppose your orders change: your fencing deliveries drop to (2, 2, 2, 2…) and your topsoil orders change to (20, 20, 20, 20). What’s going on? Make a guess if you like.
Ready?
The veggie boss figures you’ve moved to a rectangular garden, with one side determined by \( x \), and the other side a fixed 20 feet, for a 20-by-x rectangle.
Does this guess work? Assuming this is the pattern, let’s measure the perimeter, area, and how they change:
Wow, it checks out: the changes in perimeter and area match the patterns (2, 2, 2…) and (20, 20, 20…). No wonder he’s the godfather.
Lastly, what if the godfather saw topsoil orders of (5, 7, 9, 11, 13)? He might assume you’re still building a square (\( 2x + 1 \) pattern), but you started with a \( 2 \times 2 \) garden. Your first area jump was by 5, which would have happened if \( x \) was already 2 (solve \( 2x + 1 = 5 \) and we see \( x = 2 \)).
The mob boss is a master antiques dealer: he sees the pattern in the pieces you’re bringing and quickly determines the original shape (indefinite integral). The henchman can only tell you the running totals so far (definite integral).
8.4 Wrapping It All Up
It looks like we’re ready for another rule, to explain how squares change. If we leave \( dx \) as it is, we can write:
Ok! That’s the abbreviated way of saying “Grow by two sides and the corner”. Let’s plug this into the computer to check:
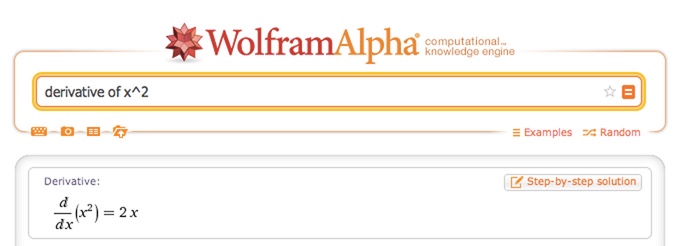
Uh oh! We hand-computed the derivative of \( x^2 \) as \( 2x + dx \) (which is usually \( 2x + 1 \)), but the computer says it’s just \( 2x \).
But isn’t the difference from \( 4^2 \) to \( 5^2 \) exactly \( 25 - 16 = 9 \), and not \( 8 \)? What happened to that corner piece? The mystery continues.