1 Minute Calculus: X-Ray and Time-Lapse Vision
We usually take shapes, formulas, and situations at face value. Calculus gives us two superpowers to dig deeper:
-
X-Ray Vision: You see the hidden pieces inside a pattern. You don’t just see the tree, you know it’s made of rings, with another growing as we speak.

- Time-Lapse Vision: You see the future path of an object laid out before you (cool, right?). “Hey, there’s the moon. For the next few days it’ll be white, but on the sixth it’ll be low in the sky, in a color I like. I’ll take a photo then.”

So how is Calculus useful? Well, just imagine having X-Ray or Time-Lapse vision to use at will. For an object or scenario we care about, how was it put together? What will happen to it down the line?
(Strangely, my letters to Marvel about Calculus-man have been ignored to date.)
Calculus In 10 Minutes: See Patterns Step-By-Step
What do X-Ray and Time-Lapse vision have in common? They examine patterns step-by-step. An X-Ray shows the individual slices inside, and a Time-Lapse puts each future state next to the other.
This seems pretty abstract. Let’s look at the equations for circumference, area, surface area, and volume:
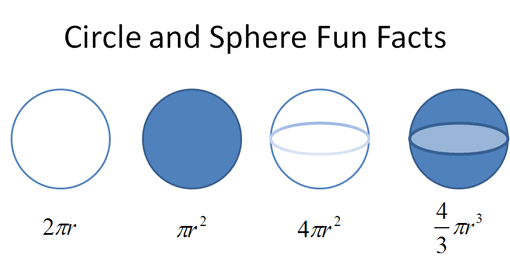
We have a vague feeling these formulas are connected, right?
Let’s turn on our X-Ray vision and see where this leads. Suppose we know $$$\textit{circumference} = 2 \pi r$$$ and we want to figure out the equation for area. What can we do?
This is a tough question. Squares are easy to measure, but how do we work out the size of an ever-curving shape?
Calculus to the rescue. Let’s use our X-Ray vision to realize a disc is really just a bunch of rings put together. Similar to a tree trunk, here’s a “step-by-step” view of a circle’s area:
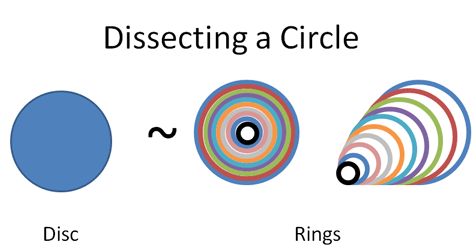
How does this viewpoint help? Well, let’s unroll those curled-up rings into straight lines, so they’re easier to measure:
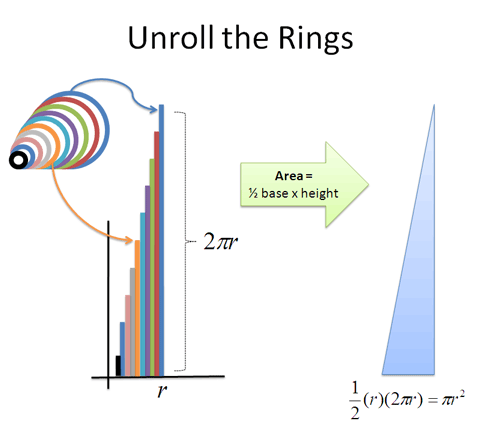
Whoa! We have a bunch of straightened-out rings that form a triangle, which is much easier to measure. (Wikipedia has an animation[^1].)
The height of each ring depends on its original distance from the center; the ring 3 inches from the center would have a height of $$$2 \pi \cdot 3$$$ inches. The smallest ring is a pinpoint, more or less, without any height at all. The height of the largest ring is the full circumference ($$$2 \pi r$$$).
And because triangles are easier to measure than circles, finding the area isn’t too much trouble. The area of the “ring triangle” = $$$\frac{1}{2} \textit{base} \cdot \textit{height} = \frac{1}{2} r (2 \pi r) = \pi r^2$$$, which is the formula for a circle’s area!
Our X-Ray vision revealed a simple, easy-to-measure structure within a curvy shape. We realized a circle and a set of glued-together rings were really the same. From another perspective, a filled-in disc is really just the “time lapse” of a single ring that grew larger.
So… What Can I Do With Calculus?
Remember learning arithmetic? You learned how to count out a number, and how to combine it with others (add/subtract, multiply/divide, take exponents/roots). Technically, counting isn’t necessary, as our caveman ancestors did “fine” (survived) without it.
But, having a specific notion of quantity makes navigating the world easier. You don’t have a “big” and “small” pile of rocks: you have an exact count. You know how many arrows can be given to each hunter, or whether the gathered berries are enough for the tribe.
Even better, arithmetic gives us metaphors that go beyond strict calculations. It has sharpened our descriptions of everything, letting us clarify everything from spiciness levels and movie ratings (1 to 5) to our mood (1 to 10). Specific measurements are a useful idea, and hard to give up once seen.
Calculus trains us in two new metaphors: splitting apart and gluing together. A pattern can be separated into parts, and the parts can be progressively combined into the full pattern.
Is this viewpoint necessary for survival? Nope. But it is interesting.
Numbers and equations describe what we have, but Calculus explains the steps that got us there. Instead of just the cookie, we can see the recipe.
Sure, Calculus appears in science because a step-by-step blueprint is more useful than being handed a final result. But in everyday scenarios, we have a nice perspective to turn on: What steps got us here? Are there any pros or cons to that approach? And based on these steps, where are we going next?
Let's feel what a Calculus perspective is like.
[^1]: Visit http://betterexplained.com/calculus/book for clickable links to extra resources.