Chapter 12 The Basic Arithmetic Of Calculus

Remember learning arithmetic? After seeing how to multiply small numbers, we learned how to multiply numbers with several digits:

\[ 13 \times 15 = (10 + 3)(10 + 5) = 100 + 30 + 50 + 15 \]

We can’t just combine the first digits (10$ \times $10) and the second (3$ \times $5) and call it done. We have to walk through the cross-multiplication.

Calculus is similar. If we have the whole function, we can blithely say that $ f(x) $ has derivative $ f'(x) $. But that isn’t illuminating, or explaining what happens behind the scenes.

If we can describe our function in terms of a building block $ x $ (such as $ f(x) = 3x^2 + x $), then we should be able to find the derivative, the pattern of changes, in terms of that same building block. If we have two types of building blocks ($ f = a \cdot b $), we’ll get the derivative in terms of those two building blocks.

Here’s the general strategy:

Imagine a scenario with a few building blocks ($ area = length \cdot width $)
Let every component change
Measure the change in the overall system
Remove the measurement artifacts (our instruments interfering with each other)

Once we know how systems break apart, we can reverse-engineer them into the integral (yay for the FTOC!).

12.1 Addition

Let’s start off easy: how does a system with two added components behave?

In the real world, this could be sending two friends (Frank and George) to build a fence. Let’s say Frank gets the wood, and George gets the paint. What’s the total cost?

\[ \textit{Total} = \textit{Frank's cost} + \textit{George's cost} \]

\[ t(x) = f(x) + g(x) \]

The derivative of the entire system, $ \frac{dt}{dx} $, is the cost per additional foot. Intuitively, we suspect the total increase is the sum of the increases in the parts:

\[ \frac{dt}{dx} = \frac{df}{dx} + \frac{dg}{dx} \]

That relationship makes sense, right? Let’s say Frank’s cost is \$3/foot for the wood, and George adds \$0.50/foot for the paint. If we ask for another foot, the total cost will increase by \$3.50.

Here’s the math for that result:

Original: $ f + g $
New: $ (f + df) + (g + dg) $
Change: $ (f + df) + (g + dg) - (f + g) = df + dg $

In my head, I imagine $ x $, the amount you requested, changing silently in a corner. This creates a visible change in $ f $ (size $ df $) and $ g $ (size $ dg $), and we see the total change as $ df + dg $.

It seems we should just combine the total up front, writing $ total = 3.5x $ not $ total = f(x) + g(x) = 3x + 0.5x $. Normally, we would simplify an equation, but it’s sometimes helpful to list every contribution (total = base + shipping + tax). In our case, we see Frank contributes the most to the price.

Remembering the derivative is the “per $ dx $” rate, we write:

\[ \frac{d}{dx} \left( f(x) + g(x) \right) = \frac{df}{dx} + \frac{dg}{dx} \]

But ugh, look at all that notation! Let’s trim it down:

Write $ f $ instead of $ f(x) $. We’ll assume a single letter is an entire function, and by the Third Edict of The Grand Math Poombahs, our functions will use a parameter $ x $.
We’ll express the derivative using a single quote ($ f' $), not with a ratio ($ \frac{df}{dx} $). We’re most interested in the relationship between the parts (addition), not the gritty details of the parts themselves.

So now the addition rule becomes:

\[ (f + g)' = f' + g' \]

Much better! Here’s how I read it: Take a system made of several parts: $ (f + g) $. The change in the overall system, $ (f + g)' $, can be found by adding the change from each part.

12.2 Multiplication

Let’s try a tricker scenario. Instead of inputs that are added (almost oblivious to each other), what if they are multiplied?

Suppose Frank and George are making a rectangular garden for you. Frank handles the width and George takes care of the height. Whenever you clap, they move… but by different amounts!

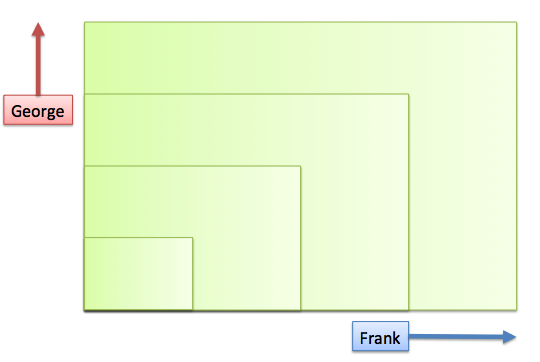
https://betterexplained.com/wp-content/uploads/calculus/course/lesson7/garden

Frank’s steps are 3-feet long, but George’s are only 2-feet long (zookeeping accident, don’t ask). How can we describe the system?

\[ \textit{Area} = \textit{width} \cdot \textit{height} = f(x) \cdot g(x) \]

\[ f(x) = 3x \]

\[ g(x) = 2x \]

We have linear parts, so the derivatives are simple: $ f'(x) = 3 $ and $ g'(x) = 2 $. What happens on the next clap?

https://betterexplained.com/wp-content/uploads/calculus/course/lesson7/garden-change

Looks familiar! We have a horizontal strip, a vertical strip, and a corner piece. We can work out the amounts with algebra:

Original: $ f \cdot g $
New: $ (f + df) \cdot (g + dg) = (f\cdot g) + (f\cdot dg) + (g\cdot df) + (df\cdot dg) $
Change: $ f\cdot dg + g\cdot df + df\cdot dg $

Let’s see this change more closely:

The horizontal strip happened when $ f $ changed (by $ df $), and $ g $ was the same value
The vertical strip was made when $ g $ changed (by $ dg $), and $ f $ was the same value
The corner piece ($ df \cdot dg $) happened when the change in one component ($ df $) interacted with the change in the other ($ dg $)

The corner piece is our sample measurement getting tangled on itself, and should be removed. (If we’re forced to move in whole units, then the corner is fine. But most real-world systems can change continuously, by any decimal number, and we want the measurement artifacts removed.)

To find the total change, we drop the $ df \cdot dg $ term (interference between the changes) and get:

\[ f \cdot dg + g \cdot df \]

I won’t let you forget the derivative is on a “per dx” basis, so we write:

\[ \frac{\textit{total change}}{dx} = f \frac{dg}{dx} + g \frac{df}{dx} \]

\[ (f \cdot g)' = f \cdot g' + g \cdot f' \]

There is an implicit “x” changing off in the distance, which makes $ f $ and $ g $ move. We hide these details to make the notation simpler.

In English: Take a scenario with multiplied parts. As they change, and continue to be multiplied, add up the new horizontal and vertical strips that are formed.

Let’s try out the rule: if we have a 12$ \times $8 garden and increment by a whole step, what change will we see?

In this case, we’ll use the discrete version of the rule since we’re forced to move as a whole step:

Vertical strip: $ f \cdot dg = 12 \cdot 2 = 24 $
Horizontal strip $ g \cdot df = 8 \cdot 3 = 24 $
Corner piece: $ df \cdot dg = 3 \cdot 2 = 6 $
Total change: $ 24 + 24 + 6 = 54 $

Let’s test it. We go from 12$ \times $8 (96 square feet) to 15$ \times $10 (150 square feet). And yep, the area increase was 150 - 96 = 54 square feet!

12.3 Simple Division (Inverses)

Inverses can be tough to visualize: as $ x $ gets bigger, $ \frac{1}{x} $ gets smaller. Let’s take it slow.

Suppose you’re sharing a cake with Frank. You’ve just cut it in half, about to take a bite and… George shuffles in. He looks upset, and you’re not about to mention the fresh set of claw marks.

But you’ve just cut the cake in half, what can you do?

Cut it again. You and Frank can cut your existing portion in thirds, and give George a piece:

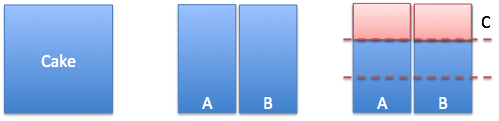
https://betterexplained.com/wp-content/uploads/calculus/course/lesson7/cake-cut

Neat! Now everyone has 1/3 of the total. You gave up 1/3 of your amount (1/2), that is, you each gave George 1/6 of the total.

Time to eat! But just as you’re about to bite in… the veggie godfather walks in. Oh, he’ll definitely want a piece. What do you do?

Cut it again. Everyone smooshes together their portion, cuts it in fourths, and hands one piece to the Don. The cake is split evenly again.

This is step-by-step thinking applied to division:

Your original share is $ \frac{1}{x} $ (when x=2, you have 1/2)
Someone walks in
Your new share becomes $ \frac{1}{x + 1} $

How did your amount of cake change? Well, you took your original slice ($ \frac{1}{x} $), cut it into the new number of pieces ($ \frac{1}{x + 1} $), and gave one away (the change is negative):

\[ \frac{1}{x} \cdot \frac{-1}{x + 1} = \frac{-1}{x(x + 1)} \]

We can probably guess that the +1 is a measurement artifact because we forced an integer change in x. If we call the test change dx, we can find the difference between the new amount ($ \frac{1}{x+1} $) and the original ($ \frac{1}{x} $):

\[ \frac{1}{x + dx} - \frac{1}{x} = \frac{x}{x(x + dx)} - \frac{x + dx}{x(x + dx)} = \frac{-dx}{x(x + dx)} \]

After finding the total change (and its annoying algebra), we divide by dx to get the change on a “per dx” basis:

\[ \frac{-1}{x(x + dx)} \]

Now we remove the leftover dx, the measurement artifact:

\[ \frac{-1}{x(x + 0)} = - \frac{1}{x^2} \]

Phew! We’ve found how an 1/x split changes as more people are added.

Let’s try it out: You are splitting a \$1000 bill among 5 people. A sixth person enters, how much money do you save?

You’ll personally save 1/5 $ \cdot $ 1/6 = 1/30 of the total cost (cut your share into 6 pieces, give the new guy one portion to pay). That’s about 3%, or 30. Not bad for a quick calculation!

Let’s work it backwards: how large is our group when we’re saving about \$100 per person? Well, \$100 is 1/10 of the total. Since $ \frac{1}{3^2} \sim \frac{1}{10} $, we’ll hit that savings rate around x=3 people.

And yep, going from 3 to 4 people means each person’s share goes from \$333.33 to \$250 – about \$100. Not bad! (If we added people fractionally, we could hit the number exactly.)

12.4 Questions

We didn’t explicitly talk about scaling by a constant, such as finding the derivative of $ f(x) = 3x $. Can you use the product rule to figure out how it changes? (Hint: imagine a rectangle with a fixed 3 for one side, and $ x $ for the other).

Now, how about the addition rule? How would $ f(x) = x + x + x $ behave?

Next → Lesson 13: Finding Patterns In The Rules