Chapter 4 Learning The Official Terms
We’ve been able to describe our thinking process with analogies (X-Rays, Time-Lapses) and diagrams:
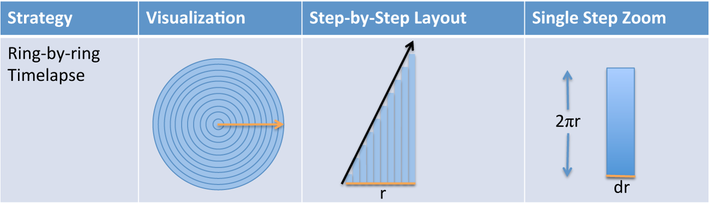
However, this is a very elaborate way to communicate. Here’s the Official Math® terms that describe our intuitive concepts:
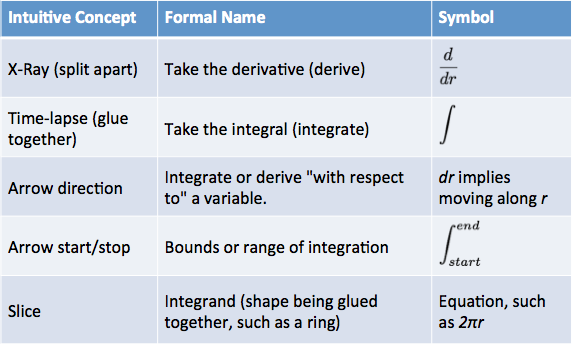
Let’s walk through the fancy names.
4.1 The Derivative
The derivative is the pattern of slices we get as we X-Ray a shape. It’s indicated by the black trend line, which might be flat, rising constantly, rising and falling, etc. Now here’s the trick: although the derivative generates the entire sequence of slices, we can also extract a single slice.
Think about a function like \( f(x) = x^2 \). It describes every possible squared value (1, 4, 9, 16, 25, etc.), and we can graph them all on a chart. But, we can also ask for the value of \( f(x) \) at a specific value, such as at \( x = 3 \).
The derivative is similar. Officially, it’s the complete pattern of slices we get after X-Raying a shape. However, we can pull out an individual slice by asking for the derivative at a certain value. (The derivative is a function, just like \( f(x) = x^2 \), and mathematicians assume you’re talking about the entire function unless you ask for a specific slice.)
So, what do we need to find the derivative? Just the shape to split apart, and the path to follow as we cut it up (the orange arrow). The terminology is “take derivative of <some pattern> with respect to <some direction>”. For example:
- The derivative of a circle with respect to the radius creates rings (which always increase)
- The derivative of a circle with respect to the perimeter creates slices (which are equal-sized)
- The derivative of a circle with respect to the x-axis creates boards (which get larger, peak, and get smaller)
I agree that “with respect to” sounds formal: Honorable Grand Poombah radius, it is with respect to you that we take the derivative. Math is a gentleman’s game, I suppose.
Taking the derivative is also called “differentiating”, because we are finding the difference between successive positions as a shape grows. As we grow the radius of a circle, the outer ring is the difference between the size of the current disc and the next size up.
4.2 The Integral, Arrows, and Slices
The integral is gluing together (Time-Lapsing) a bunch of slices and measuring the final result. For example, we glued together the rings (into a “ring triangle”) and saw it accumulated to \( \pi r^2 \), aka the area of a circle.
Here’s what we need to find the integral:
- Which direction are we gluing the steps together? Along the orange line (the radius, in this case)
- When do we start and stop? At the start and end of the arrow (we start at 0, no radius, and move to r, the full radius)
- How big is each step? Well… each item is a “ring”. Isn’t that enough?
Nope! We need to be specific. We’ve been saying we cut a circle into “rings” or “pizza slices” or “boards”. But that’s not specific enough; it’s like a BBQ recipe that says “Cook meat. Flavor to taste.”
Maybe an expert knows what to do, but we need more specifics. How large, exactly, is each step (technically called the “integrand”)?

Ah. A few notes about the variables:
- If we are moving along the radius \( r \), then \( dr \) is the little chunk of radius in the current step
- The height of the ring is the circumference, or \( 2 \pi r \)
There’s several gotchas to keep in mind.
First, \( dr \) is its own variable, and not “d times r”. It represents the tiny section of the radius present in the current step. This symbol (\( dr \), \( dx \), etc.) is often separated from the integrand by just a space, and it’s assumed to be multiplied (written \( 2 \pi r \ dr \)).
Next, if \( r \) is the only variable used in the integral, then \( dr \) is assumed to be there. So if you see \( \int 2 \pi r \) this still implies we’re doing the full \( \int 2 \pi r \ dr \). (Again, if there are two variables involved, like radius and perimeter, you need to clarify which step we’re using: \( dr \) or \( dp \)?)
Last, remember that \( r \) (the radius) changes as we Time-Lapse, starting at 0 and eventually reaching its final value. When we see \( r \) in the context of a step, it means “the size of the radius at the current step” and not the final value it may ultimately have.
These issues are extremely confusing. I’d prefer we use \( r_{dr} \) for “\( r \) at the current step” instead of a general-purpose \( r \) that’s easily confused with the max value of the radius. We can’t change the symbols at this point, unfortunately.
4.3 Practicing The Lingo
Let’s learn to speak like calculus natives. Here’s how we can describe our X-Ray strategies:
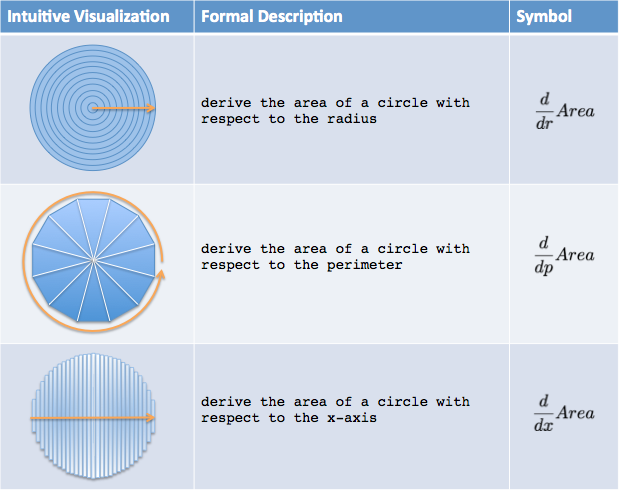
Remember, the derivative just splits the shape into (hopefully) easy-to-measure steps, such as rings of size \( 2 \pi r \ dr \). We broke apart our lego set and have pieces scattered on the floor. We still need an integral to glue the parts together and measure the new size. The two commands are a tag team:
- The derivative says: “Ok, I split the shape apart for you. It looks like a bunch of pieces \( 2 \pi r \) tall and \( dr \) wide.”
- The integral says: “Oh, those pieces resemble a triangle – I can measure that! The total area of that triangle is \( \frac{1}{2} \textit{base} \cdot \textit{height} \), which works out to \( \pi r^2 \) in this case.”
Here’s how we’d write the integrals to measure the steps we’ve made:
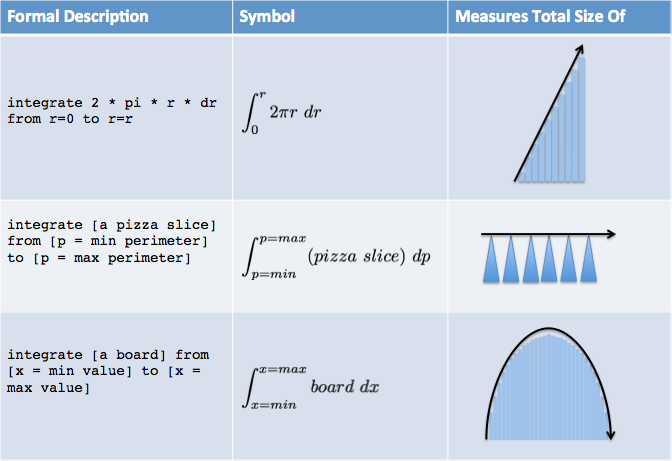
A few notes:
- Often, we write an integrand as an unspecified “pizza slice” or “board” (use a formal-sounding name like \( s(p) \) or \( b(x) \) if you like). First, we setup the integral, and then we worry about the exact formula for a board or slice.
- Because each integral represents slices from our original circle, we know they will be the same. Gluing any set of slices should always return the total area, right?
- The integral is often described as “the area under the curve”. It’s accurate, but shortsighted. Yes, we are gluing together the rectangular slices under the curve. But this completely overlooks the preceding X-Ray and Time-Lapse thinking. Why are we dealing with a set of slices vs. a curve in the first place? Most likely, because those slices are easier than analyzing the shape itself (how do you “directly” measure a circle?).
4.4 Questions
At a high level, can you find another activity made easier with symbols, instead of using full English sentences? Would practitioners ever go back to written descriptions?
Math is just like that. Let’s try a few phrases, even if we aren’t fluent yet.
Question 1: Can you describe the integrals below in “Math English”?
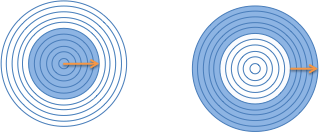
Assume the arrow spans half the radius. The description should follow the format:
integrate [size of step] from [start] to [end] with respect to [path variable]
Have an idea? Here’s the answer for the first integral1 and the second integral2. These links go to Wolfram Alpha, an online math solver, which we’ll learn to use.
Question 2: Can you find the “Math English” way to describe our pizza-slice idea?
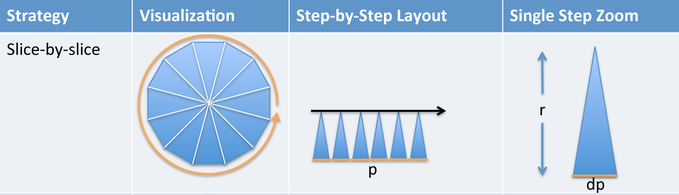
The math description should be something like this:
integrate [size of step] from [start] to [end] with respect to [path variable]
Remember that each slice is basically a triangle (so what’s the area?). The slices move around the perimeter (where does it start and stop?). Have a guess for the command? Here it is, the slice-by-slice description3.
Question 3: Can you describe how to move from volume to surface area?
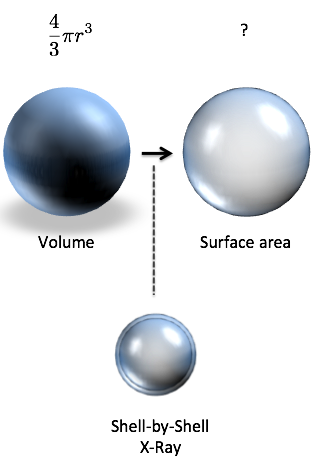
Assume we know the volume of a sphere is 4/3 * pi * r⌃3. Think about
the instructions to separate that volume into a sequence of shells. Which variable are we moving through?
take derivative of [equation] with respect to [path variable]
Have a guess? Great. Here’s the command to turn volume into surface area4.