Chapter 3 Expanding Our Intuition
I hope you thought about the question from last time: how do we take our X-Ray strategies into the 3rd dimension?
Here’s my take:

- Rings become shells, a thick candy coating on a delicious gobstopper. Each layer is slightly bigger than the one before.
- Slices become wedges, identical sections like slices of an orange.
- Boards become plates, thick discs which can be stacked together. (I sometimes daydream of opening a bed & breakfast that only serves spherical stacks of pancakes.)
The 3d segments can be seen as being made from their 2d counterparts. For example, we can spin an individual ring like a coin to create a shell. A wedge looks like a bunch of pizza slices (of different sizes) stacked on top of each other. Lastly, we can imagine spinning a board to make a plate, like carving a wooden sphere with a lathe (video).
The tradeoffs in 3d are similar to the 2d versions:
- Organic processes grow in shell-by-shell layers (pearls in an oyster).
- Fair divisions require wedges (cutting an apple for friends).
- The robotic plate approach seems easy to manufacture (weightlifting plates).
An orange is an interesting hybrid: from the outside, it appears to be made from shells, growing over time. But on the inside, it forms a symmetric internal structure with wedges – good for evenly distributing seeds, right? We could analyze it both ways.
3.1 Exploring The 3d Perspective
In the first lesson we had the vague notion that the circle/sphere formulas were related:
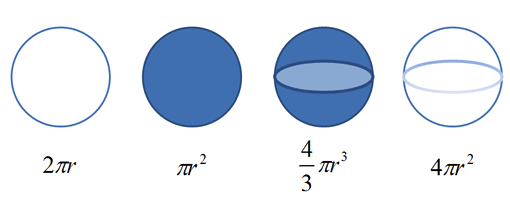
With our X-Ray and Time-Lapse skills, we have a specific idea for how:
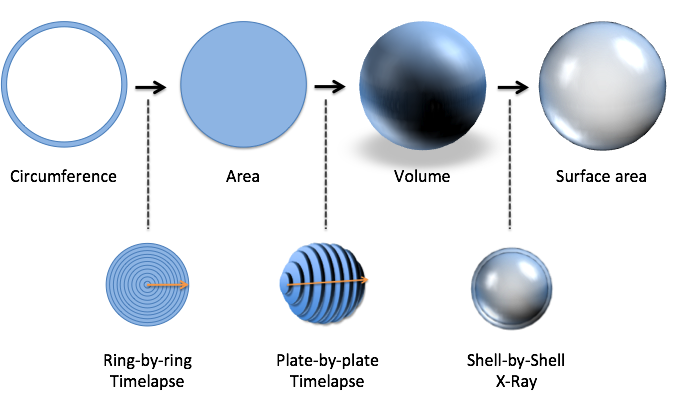
- Circumference: Start with a single ring.
- Area: Make a filled-in disc with a ring-by-ring time lapse.
- Volume: Make the circle into a plate, and do a plate-by-plate time lapse to build a sphere.
- Surface area: X-Ray the sphere into a bunch of shells; the outer shell is the surface area.
Wow! We now have detailed descriptions of how one formula is related to the other. We know, intuitively, how to morph shapes into alternate versions by thinking “Time-Lapse this” or “X-Ray that”. We could even work backwards: starting with a sphere, we can X-Ray it into plates, and then take one plate and X-Ray it into rings.
3.2 The Need For Math Notation
You might have noticed it’s getting harder to describe your ideas. We’re reaching for physical analogies (rings, boards, wedges) to explain our plans: “Ok, take that circular area, and try to make some discs out of it. Yeah, like that. Now line those discs up into the shape of a sphere…”.
I love diagrams and analogies, but should they be required to explain an idea? Probably not.
Take a look at how numbers developed. At first, we used very literal symbols for counting: I, II, III, and so on. Eventually, we realized a symbol like V could take the place of IIIII, and even better, every digit can have its own symbol. (The number “1” reminds us of our line-based history.)
Math notation helped in a few ways:
- Symbols are shorter than words. Isn’t “2 + 3 = 5” better than “two added to three is equal to five”? Fun fact: In 1557, Robert Recorde invented the equals sign, written with two parallel lines (=), because “noe 2 thynges, can be moare equalle”. (I agrye!)
- The rules do the work for us. With Roman numerals, we’re essentially recreating numbers by hand (why should VIII take so much effort to write compared to I? Just because 8 is larger than 1? Not a good reason!). Decimals help us “do the work” of expressing numbers, and make them easy to manipulate. So far, we’ve been doing the work of calculus ourselves: cutting a circle into rings, realizing we can unroll them, looking up the equation for area and measuring the resulting triangle. Couldn’t the rules help us here? You bet. We just need to figure them out.
- We generalized our thinking. “2 + 3 = 5” is really “twoness + threeness = fiveness”. It sounds weird, but we have an abstract quantity (not people, or money, or cows… just “twoness”) and we see how it’s related to other quantities. The rules of arithmetic are general-purpose, and it’s our job to apply them to a specific scenario.
This last point is important. When learning addition, your teacher may have used literal apples to show that two plus three was five. With enough practice, you started using abstract symbols without needing a physical example, and “2 + 3 = 5” made sense.
Calculus is similar: it works on abstract equations like \( f(x) = x^2 \), but physical examples are a nice starting point. When we see a shape like this:

we can actually see what Calculus does as we apply a technique, instead of pushing symbols around. Eventually, we can convert the shape into its corresponding equation and work with symbols directly.
So, don’t think Calculus requires a real-world object, any more than addition requires apples. It can analyze any shape or formula (a physics equation, business scenario, graph of a function) – shapes are just easier to start with.