Chapter 15 Discovering Archimedes’ Formulas
In the preceding lessons we uncovered a few calculus relationships, the “arithmetic” of how systems change:
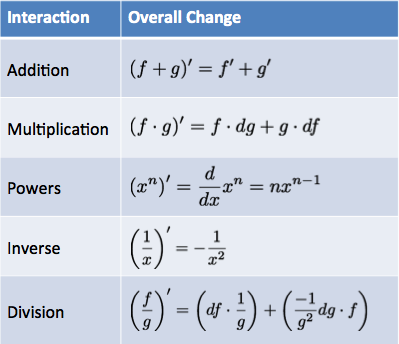
How do these rules help us?
- If we have an existing equation, the rules are a shortcut to finding the step-by-step pattern. Instead of visualizing a growing square, or cube, the Power Rule lets us crank through the derivatives of \( x^2 \) and \( x^3 \). Whether \( x^2 \) refers to a literal square or just the multiplication \( x \cdot x \) isn’t important – we’ll get the pattern of changes.
- If we have a set of changes, the rules help us reverse-engineer the original pattern. Getting changes like \( 2x \) or \( 14x \) is a hint that \( \textit{something} \cdot x^2 \) was the original pattern.
Learning to think with Calculus means we can use X-Ray and Time-lapse vision to imagine changes taking place, and use the rules to work out the specifics. Eventually, we might not visualize anything, and just work with the symbols directly (as you likely do with arithmetic today).
In the start of the course, we morphed a ring into a circle, then a sphere, then a shell:
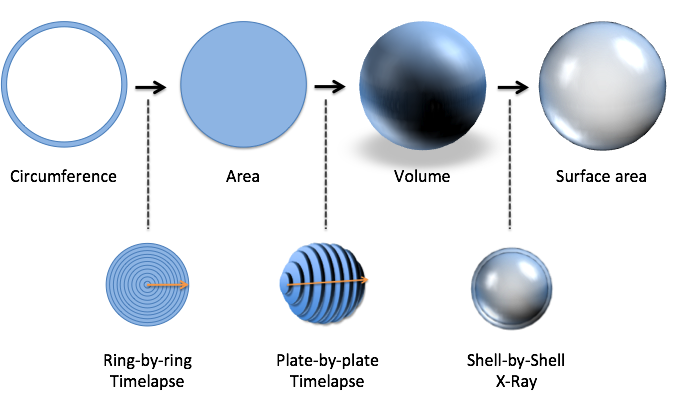
With the official rules in hand, we can blast through the calculations and find the circle/sphere formulas on our own. It may sound strange, but the formulas feel different to me – almost alive – when you see them morphing in front of you. Let’s jump in.
15.1 Changing Circumference To Area
Our first example of “step-by-step” thinking was gluing a sequence of rings to make a circle:

When we started, we needed a lot of visualization. We had to unroll the rings, line them up, realize they made a triangle, then use \( \frac{1}{2} \textit{base} \cdot \textit{height} \) to get the area. Visual, tedious… and necessary. We need to feel what’s happening before working with raw equations.
Here’s the symbolic approach:

Let’s walk through it. The notion of a “ring-by-ring timelapse” sharpens into “integrate the rings, from nothing to the full radius” and ultimately:
Each ring has height \( 2 \pi r \) and width \( dr \), and we want to accumulate that area to make our disc.
How can we solve this equation? By working backwards. We can move the \( 2 \pi \) part outside the integral (remember the scaling property?) and focus on the integral of \( r \):
What pattern makes steps of size \( r \)? Well, we know that \( r^2 \) creates steps of size \( 2r \), which is twice what we need. Half that should be perfect. Let’s try it out:
Yep, \( \frac{1}{2}r^2 \) gives us the steps we need! Now we can plug in the solution to the integral:
This is the same result as making the ring-triangle in the first lesson, but we manipulated equations, not diagrams. Not bad! It’ll help even more once we get to 3d…
15.2 Changing Area To Volume
Let’s get fancier. We can take our discs, thicken them into plates, and build a sphere:
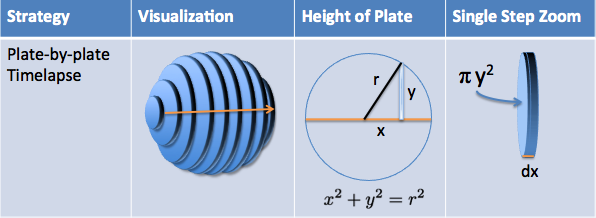
Let’s walk slowly. We have several plates, each at a different “x-coordinate”. What’s the size of a single plate?
The plate has a thickness (\( dx \)), and its own radius. The radius of the plate is its height from the x-axis, which we can call \( y \).
It’s a little confusing at first: \( r \) is the radius of the entire sphere, but \( y \) is the (usually smaller) radius of an individual plate under examination. In fact, only the center plate (\( x=0 \)) will have its radius the same as the entire sphere. The “end plates” don’t have a height at all.
And by the Pythagorean theorem, we have a connection between the x-position of the plate, and its height (\( y \)):
Ok. We have size of each plate, and can integrate to find the volume, right?
Not so fast. Instead of starting on the left side, with a negative x-coordinate, moving to 0, and then up to the max, let’s just think about a sphere as two halves:

To find the total volume, get the volume of one half, and double it. This is a common trick: if a shape is symmetrical, get the size of one part and scale it up. Often, it’s easier to work out “0 to max” than “min to max”, especially when “min” is negative.
Ok. Now let’s solve it:

Whoa! Quite an equation, there. It seems like a lot, but we’ll work through it:
First off, three variables (\( r \), \( y \), \( x \)) is too many to have flying around in a single equation. We’ll write the height of each plate (\( y \)), in terms of the others:
The square root looks intimidating at first, but it’s being plugged into \( y^2 \) and the exponent will cancel it out. After plugging in y and moving \( \pi \) outside the integral, we have the much nicer:
The parentheses are often dropped because it’s understood that \( dx \) is multiplied by the entire size of the step. We know the step is \( (r^2 - x^2) dx \) and not \( r^2 - (x^2 dx) \).
Let’s talk about \( r \) and \( x \) for a minute. \( r \) is the radius of the entire sphere, such as “15 inches”. You can imagine asking “I want the volume of a sphere with a radius of 15 inches”. Fine.
To figure this out, we’ll create plates at each x-coordinate, from \( x=0 \) up to \( x=15 \) (and double it). \( x \) is the bookkeeping entry that remembers which plate we’re on. We could work out the volume from \( x=0 \) to \( x=7.5 \), let’s say, and we’d build a partial sphere (maybe useful, maybe not). But we want the whole shebang, so we let \( x \) go from 0 to the full \( r \).
Time to solve this bad boy. What equation has steps like \( r^2 - x^2 \)?
First, let’s use the addition rule: steps like \( a - b \) are made from two patterns (one making \( a \), the other making \( b \)).
Let’s look at the first pattern, the steps of size \( r^2 \). We’re moving along the x-axis, and \( r \) is a number that never changes: it’s 15 inches, the size of our sphere. This max radius never depends on \( x \), the position of the current plate.
When a scaling factor doesn’t change during the integral (\( r \), \( \pi \), etc.), it can be moved outside and scaled up at the end. So we get:
In other words, \( r^2 \cdot x \) is a linear trajectory that contributes a constant \( r^2 \) at each step.
Cool. How about the integral of \( -x^2 \)? First, we can move out the negative sign and take the integral of \( x^2 \):
We’ve seen this before. Since \( x^3 \) has steps of \( 3x^2 \), taking 1/3 of that amount (\( \frac{x^3}{3} \)) should be just right. And we can check that our integral is correct:
It works out! Over time, you’ll learn to trust the integrals you reverse-engineer, but when starting out, it’s good to check the derivative. With the integrals solved, we plug them in:
What’s left? Well, our formula still has \( x \) inside, which measures the volume from 0 to some final value of \( x \). In this case, we want the full radius, so we set \( x=r \):
Tada! You’ve found the volume of a sphere (or another portion of a sphere, if you use a different range for \( x \)).
Think that was hard work? You have no idea. That one-line computation took Archimedes, one of the greatest geniuses of all time, tremendous effort to figure out. He had to imagine some spheres, and a cylinder, and some cones, and a fulcrum, and imagine them balancing and… let’s just say when he found the formula, he had it written on his grave. Your current intuition would have saved him incredible effort (see this video).
15.3 Changing Volume To Surface Area
Now that we have volume, finding surface area is much easier. We can take a thin “peel” of the sphere with a shell-by-shell X-Ray:
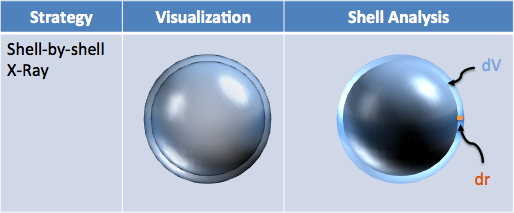
I imagine the entire shell as “powder” on the surface of the existing sphere. How much powder is there? It’s \( dV \), the change in volume. Ok, what is the area the powder covers?
Hrm. Think of a similar question: how much area will a bag of mulch cover? Get the volume, divide by the desired thickness, and you have the area covered. If I give you 300 cubic inches of dirt, and spread it in a pile 2 inches thick, the pile will cover 150 square inches. After all, if \( \textit{Area} \cdot \textit{Thickness} = \textit{Volume} \) then \( \textit{Area} = \frac{Volume}{Thickness} \).
In our case, \( dV \) is the volume of the shell, and \( dr \) is its thickness. We can spread \( dV \) along the thickness we’re considering (\( dr \)) and see how much area we added: \( \frac{dV}{dr} \), the derivative.
This is where the right notation comes in handy. We can think of the derivative as an abstract, instantaneous rate of change (\( V' \)), or as a specific ratio (\( \frac{dV}{dr} \)). In this case, we want to consider the individual elements, and how they interact (volume of shell / thickness of shell).
So, given the relation,
we figure out:
Wow, that was fast! The order of our morph (Circumference \( \rightarrow \) Area \( \rightarrow \) Volume \( \rightarrow \) Surface area) made the last step simple. We could try to spin a circumference into surface area directly, but it’s more complex.
As we cranked through this formula, we “dropped the exponent” on \( r^3 \) to get \( 3 r^2 \). Remember the total change comes from 3 perspectives that contribute an equal share: \( \frac{d}{dr} r^3 = r^2 + r^2 + r^2 = 3r^2 \).
15.4 2000 Years Of Math In A Day
The steps we worked through took 2000 years of thought to discover, by the greatest geniuses no less. Calculus is such a broad and breathtaking viewpoint that it’s difficult to imagine where it doesn’t apply. It’s just about using X-Ray and Time-Lapse vision:
- Break things down. In your current situation, what’s the next thing that will happen? And after that? Is there a pattern here? (Getting bigger, smaller, staying the same.) Is that knowledge useful to you?
- Find the source. You’re seeing a bunch of changes – what caused them? If you know the source, can you predict the end-result of all the changes? Is that prediction helpful?
We’re used to analyzing equations, but I hope it doesn’t stop there. Numbers can describe mood, spiciness, and customer satisfaction; step-by-step thinking can describe battle plans and psychological treatment. Equations and geometry are just nice starting points to analyze. Math isn’t about equations, and music isn’t about sheet music – they point to the idea inside the notation.
While there are more details for other derivatives, integration techniques, and how infinity works, you don’t need them to start thinking with Calculus. What you discovered today would have brought a tear to Archimedes’ eye, and that’s a good enough start for me.
Happy math.