Chapter 2 Practicing X-Ray and Time-Lapse Vision
Calculus trains us to use X-Ray and Time-Lapse vision, such as re-arranging a circle into the “ring triangle” we saw in the previous chapter. This makes finding the area… well, if not exactly easy, much more manageable.
But we were a little presumptuous. Must every circle in the universe be made from rings?
Heck no! We’re more creative than that. Here’s a few more ways we could have X-Rayed the circle:
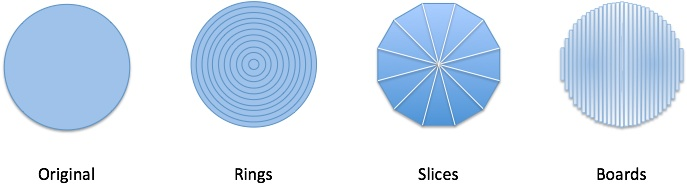
We could imagine a circle as a set of rings, pizza slices, or vertical boards. Each blueprint is a different step-by-step strategy in action.
2.1 Ring-by-ring Analysis
Using your Time-Lapse vision, imagine how the ring-by-ring strategy accumulates over time:

What’s interesting about a ring-by-ring progression?
- Each intermediate stage is an entire “mini circle” on its own. i.e., when we’re halfway done, we still have a circle, just one with half the regular radius.
- Each step is an increasing amount of work. Just imagine plowing a circular field and spreading the work over several days. On the first day, you start at the center and don’t even move. The next, you make take the tightest turn you can. Then you start doing laps, larger and larger, until you are circling the entire yard on the last day.
- The work is reasonably predictable, which may help planning. If we know it’s an extra minute for each lap, then the 20th ring will take 20 minutes.
- Most of the work happens in the final laps. In the first 25% of the timelapse, we’ve barely grown: we’re adding tiny rings. Near the end, we start to pick up steam by adding long rings, each nearly the final size.
Now let’s get practical: why do trees follow a ring pattern?
A big tree must grow from a complete smaller tree. With the ring-by-ring strategy, we’re always building on a complete, fully-formed circle. We aren’t trying to grow the “left half” of the tree and then work on the right side.
In fact, many natural processes that grow (trees, bones, bubbles, etc.) take this inside-out approach.
2.2 Slice-by-slice Analysis

Now think about a slice-by-slice progression. What do you notice?
- We contribute the same amount with each step. Even better, the parts are identical. This may not matter for math, but in the real world (e.g., cutting a cake), we want to use the same motion when cutting each slice.
- Because the slices are symmetrical, we can use shortcuts like making cuts across the entire shape. These “assembly line” speedups work well when generating identical components.
- Progress is extremely easy to measure. If we have 10 slices, then at slice 6 we are exactly 60% done (by both area and circumference).
- We follow a sweeping circular path, never retracing our steps from an “angular” point of view. When carving out the rings, each step involved the full 360 degrees.
Let’s think about the real world: what objects use the slice-by-slice pattern, and why?
Well food, for one. Cake, pizza, pie: we want everyone to have an equal share. Slices are simple to cut, we get nice speedups (cutting across the cake), and it’s easy to see how much is remaining. Imagine cutting circular rings from a pie and estimating how much is left.
Now think about radar scanners: they sweep a beam in a circle, “clearing” a slice of sky before moving to another angle. This strategy does leave a blind spot in the angle you haven’t yet covered, a tradeoff you’re hopefully aware of.
Contrast this to sonar used by a submarine or bat, which sends a sound “ring” propagating in every direction. That works best for close targets (covering every direction at once). The drawback is that unfocused propagation gets much weaker the further out you go, as the initial energy is spread out over a larger ring. We use megaphones and antennas to focus our signals into beams (thin slices) to get the most range for our energy.
Logistically, if we’re building a circular shape from a set of slices (like the folded sections of a paper fan), it helps to have every part be identical. Figure out the best way to make a single slice, then mass produce them. Even better: if one part can collapse, the entire shape can fold up!
2.3 Board-by-board Analysis

Getting the hang of X-Rays and Time-lapses? Great. Look at the progression above, and spend a few seconds thinking of the pros and cons. Don’t worry, I’ll wait.
Ready? Ok. Here’s a few of my observations:
- This is a very robotic pattern, with boards neatly arranged left-to-right.
- The contribution from each step starts small, gradually gets larger, maxes out in the middle, and begins shrinking again.
- Our progress is somewhat unpredictable. Sure, at the halfway mark we’ve finished half the circle, but the pattern rises and falls which makes it difficult to analyze. By contrast, the ring-by-ring pattern changed the same amount each time, always increasing. It was clear that the later rings would add the most work. Here, it’s the middle section which seems to be doing the heavy lifting.
Ok, time to figure out where this pattern shows up in the real world.
Decks and wooden structures, for one. When putting down wooden planks, we don’t want to retrace our steps (especially if there are other steps involved, like painting). Just like a tree needs a fully-formed circle at each step, a deck insists upon using the linear boards we can find at Home Depot.
In fact, any process with a strict “pipeline” might use this approach: finish a section and move onto the next. Think about a printer that has to spray a pattern as the paper is fed through (or these days, a 3d printer). The printer sees a position only once, so it better make it count!
The circle doesn’t need to be a literal shape. It could represent a goal you’re trying to accomplish, whether an exercise plan or topics to cover in a counseling session.
The board approach suggests you start small, work your way up, then ease back down. The pizza-slice approach could be tolerable (identical progress every day), but rings could be demoralizing: every step requires more effort than the one before.
2.4 Getting Organized
So far, we’ve been using natural descriptions to explain our thoughts: “Take a bunch of rings” or “Cut the circle into pizza slices”. This conveys a general notion, but it’s a bit like describing a song with “Dum-de-dum-dum” – you’re probably the only one who knows what you mean. But a little organization can make your intent perfectly clear.
To start, we can explain how we’re splitting the shape into steps. I like to imagine a little arrow in the direction we move as we cut out each piece:
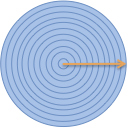
In my head, I’m moving along the yellow line, calling out the steps as we go (step forward, make a ring, step forward, make a ring…).
And while the arrow shows how the rings are made, the steps are hard to visualize because they’re jammed inside the circle. As we saw in the first lesson, we can pull out the individual steps and line them up:
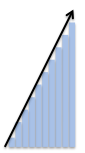
We draw a black arrow to show the trend in the size of each step. Pretty nice, right? We can tell, at a glance, that the rings are increasing, and by the same amount each time (the trend line is straight, like a set of stairs).
Math fans and neurotics both enjoying lining up the pieces. There is something soothing about it, I suppose: who doesn’t want to line up all the pencils that are scattered on the floor?
And since we’re on the topic, we might as well organize the other patterns too:
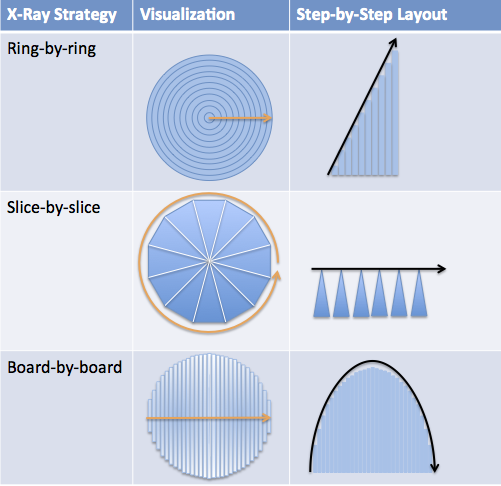
Ah! Now it’s much easier to compare each X-Ray strategy:
- With circular rings, steps increase steadily (upward sloping line)
- With triangular slices, steps stay the same size (flat, horizontal line)
- With rectangular boards, steps get larger, peak, then get smaller (up and down). The trend line looks elongated because the boards have been pushed down to line up at the bottom.
These charts make the strategy comparisons easier, wouldn’t you say? Sure. But wait, isn’t that trendline looking like a dreaded x-y graph?
Yep. Unfortunately, many classes simply present the black trend line, without showing you the pieces it represents. That’s a recipe for pain: be explicit about what the graph means!
The black trend line is the super-summarized description of an X-Ray strategy. We’re showing the size of each piece (the graph height) and how their size is changing (trend direction).
The distinction between a ring, slice and board isn’t important: in Calculus, they’re all pieces of the whole pattern. Words like “slice”, “ring” or “board”, are just descriptive versions of “piece of the whole”, and are otherwise interchangeable.
In this guide we’ll keep graphs to the level seen above: trend lines, with the individual pieces shown. This is a foundation for later, performance-based classes where you may work with graphs directly. But just for reference, Archimedes laid the foundations of Calculus without x-y graphs, and found his results without them.
2.5 Questions
Are things starting to click a bit? Thinking better with X-Rays and Time-lapses?
- Can you describe a grandma-friendly version of what you’ve learned?
- Let’s expand our thinking into the 3rd dimension. Can you think of a few ways to build a sphere? (No formulas, plain-English descriptions are fine.)
PS. It may bother you that our steps create a “circle-like” shape, but not a real, smooth circle. Great question, and we’ll get to that. But to be fair, it must also bother you that the square pixels on a computer screen make “letter-like” patterns, but not real, smooth letters. And somehow, the “letter-like patterns” convey the same information as real letters!