Chapter 9 Working With Infinity
Last time, we manually worked on the derivative of \( x^2 \) as \( 2x + 1 \). But the official derivative, according to the calculator, was \( 2x \). What gives?
The answer relies on the concept of infinite accuracy. Infinity is a fascinating and scary concept – there are entire classes (Analysis) that study it. We’ll avoid the theoretical nuances: our goal is a practical understanding of how infinity helps us with Calculus.
9.1 Insight: Sometimes Infinity Can Be Measured
Here’s a quick brainteaser for you. Two friends are 10 miles apart, moving towards each other at 5mph each. A mosquito files quickly between them, touching one person, then the other, on and on, until the friends high-five and the mosquito is squished.
Let’s say the mosquito travels a zippy 20mph as it goes. Can you figure out how far it flew before its demise?

Yikes. This one is tricky: once the mosquito leaves the first person, touches the second, and turns around… the first person has moved closer! We have an infinite number of ever-diminishing distances to add up. The question seems painfully difficult to solve, right?
Well, how about this reasoning: from the perspective of the people walking, they’re going to walk for an hour total. After all, they start 10 miles apart, and the gap shrinks at 10 miles per hour (5mph + 5mph). Therefore, the mosquito must be flying for an hour, and go 20 miles.
Whoa! Did we just find the outcome of a process with an infinite number of steps? I think so!
9.2 Splitting A Whole Into Infinite Parts
It’s time to turn our step-by-step thinking into overdrive. Can we think about a finite shape being split into infinite parts?
- In the beginning of the course, we saw a circle could be split into rings. How many? Well, an infinite number!
- A number line can be split into an infinite number of neighboring points. How many decimals would you say there are between 1.0 and 2.0?
- The path of a mosquito can be seen as a whole, or a journey subdivided into an infinite number of segments.
When we have two viewpoints (the mosquito, and the walkers), we can pick the one that’s easier to work with. In this case, the walker’s holistic viewpoint is simpler. With the circle, it’s easier to think about the rings themselves. It’s nice to have both options available.
Here’s another example: can you divide a cake into 3 equal portions, by only cutting into quarters?

It’s a weird question… but possible! Cut the entire cake into quarters. Share 3 pieces and leave 1. Cut the remaining piece into quarters. Share 3 pieces, leave 1. Keep repeating this process: at every step, everyone has received an equal share, and the remaining cake will be split evenly as well. Wouldn’t this plan maintain an even split among 3 people?
We’re seeing the intuition behind infinite X-Ray and Time-lapse vision: zooming in to turn a whole into an infinite sequence. At first, we might think dividing something into infinite parts requires each part to be nothing. But, that’s not right: the number line can be subdivided infinitely, yet there’s a finite gap between 1.0 and 2.0.
9.3 Two Fingers Pointing At The Same Moon
Why can we understand variations of the letter A, even when pixelated?
Even though the rendering is different, we see the idea being pointed to. All three versions, from perfectly smooth to jagged, create the same letter A in our heads (or, are you unable to read words when written out with rectangular pixels?). An infinite sequence can point to the same result we’d find if we took it all at once.
In calculus, there are detailed rules about how to find what result an infinite set of steps points to. And, there are certain sequences that cannot be worked out. But, for this primer, we’ll deal with functions that behave nicely.
We’re used to jumping between finite representations of the same idea (5 = V = IIIII). Now we’re seeing we can convert between a finite and infinite representation of an idea, similar to \( \frac{1}{3} = .333\ldots = .3 \ + \ .03 \ + \ .003 \ + \ \ldots \).
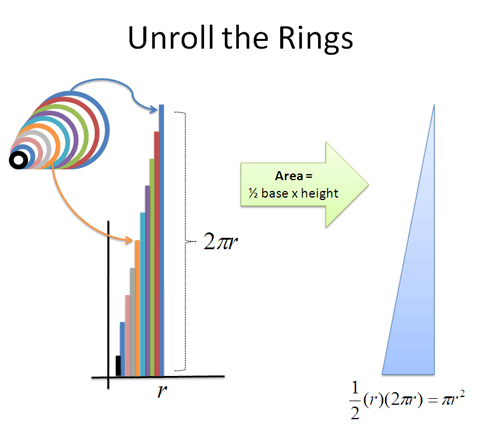
When we turned a circle into a ring-triangle, we said “The infinitely-many rings in our circle can be turned into the infinitely-many boards that make up a triangle. And the resulting triangle is easy to measure.”
Today’s goal isn’t to become an expert on infinity. It’s to intuitively appreciate a few practical conclusions:
- Infinitely many parts can combined to a finite result, if they decrease fast enough
- A process with limited (but improving) precision can point to the same result as one with infinite precision
In Calculus terms, this means the conclusions drawn from our finite (but growing) sequence of steps can be trusted1.
- Calculus is a powerful but not flawless tool. Jumpy, artificial patterns trip it up and can’t be analyzed. Luckily, most naturally-occurring patterns can be. ↑