Chapter 6 Improving Arithmetic And Algebra
We’ve intuitively seen how calculus dissects problems with a step-by-step viewpoint. Now that we have the official symbols, let’s see how to bring arithmetic and algebra to the next level.
6.1 Better Multiplication And Division
Multiplication makes addition easier. Instead of grinding through questions like 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2, we can rewrite it as: 2 \( \times \) 13.
Boomshakalaka. If you wanted 13 copies of a number, just write it like that!
Multiplication makes repeated addition easier. But there’s a big limitation: we must use identical, average-sized pieces.
- What’s 2 \( \times \) 13? It’s 13 copies of the same element.
- What’s 100 / 5? It’s 100 split into 5 equal parts.
Identical parts are fine for textbook scenarios, where you drive an unwavering 30mph for exactly 3 hours. The real world isn’t so smooth. Calculus lets us accumulate or separate shapes according to their actual, not average, amount:
- The derivative is a better type of division that splits a shape along a path (into possibly different-sized slices)
- The integral is a better type of multiplication that accumulates a sequence of steps (which could be different sizes)
| Operation | Example | Notes |
| Division | \( \dfrac{y}{x} \) | Split whole into identical parts |
| Differentiation | \( \dfrac{d}{dx} y \) | Split whole into (possibly different) parts |
| Multiplication | \( y \cdot x \) | Accumulate identical steps |
| Integration | \( \int y \ dx \) | Accumulate (possibly different) steps |
Let’s analyze our circle-to-ring example again. How does arithmetic/algebra compare to calculus?
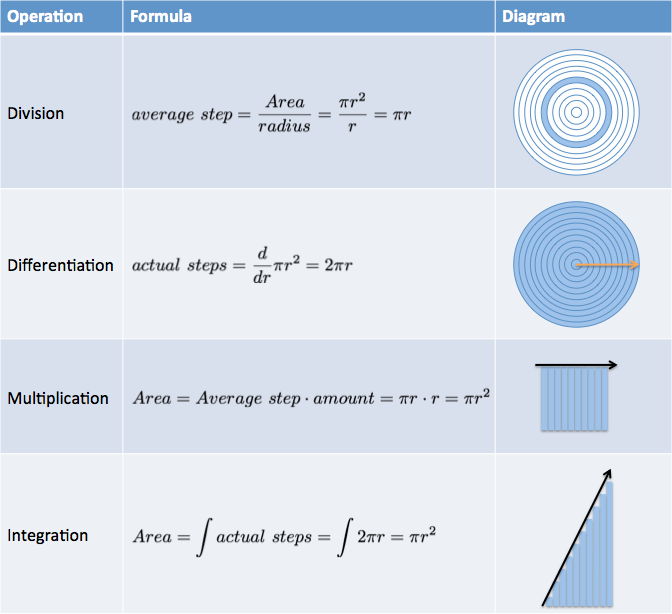
Division spits back the averaged-sized ring in our pattern. The derivative gives a formula (\( 2 \pi r \)) that describes every ring (just plug in r). Similarly, multiplication lets us scale up the average element (once we’ve found it) into the full amount. Integrals let us add up the pattern directly.
Sometimes we want to use the average item, not the fancy calculus steps, because it’s a simpler representation of the whole (“What’s the average transaction size? I don’t need the full list.”). That’s fine, as long as it’s a conscious choice.
6.2 Better Formulas
If calculus provides better, more-specific version of multiplication and division, shouldn’t we rewrite formulas with it? You bet.
| Algebra | Calculus |
| \( \textit{distance} = \textit{speed} \cdot \textit{time} \) | \( \textit{distance} = \int \textit{speed} \ dt \) |
| \( \textit{speed} = \dfrac{\textit{distance}}{\textit{time}} \) | \( \textit{speed} = \dfrac{d}{dt} \textit{distance} \) |
| \( \textit{area} = \textit{height} \cdot \textit{width} \) | \( \textit{area} = \int \textit{height} \ dw \) |
| \( \textit{weight} = \textit{density} \cdot \textit{length} \cdot \textit{width} \cdot \textit{height} \) | \( \textit{weight} = \iiint \textit{density} \ dx \ dy \ dz \) |
An equation like \( \textit{distance} = \textit{speed} \cdot \textit{time} \) explains how to find total distance assuming an average speed. An equation like \( \textit{distance} = \int \textit{speed} \ dt \) tells us how to find total distance by breaking time into instants (split along the “t” axis), and accumulating the (potentially unique) distance traveled each instant (\( \textit{speed} \cdot dt \)).
Similarly, \( \textit{speed} = \frac{d}{dt} \textit{distance} \) explains that we can split our trajectory into time segments, and the (potentially unique) amount we moved in that time slice was the speed.
The overused “integrals are area under the curve” explanation becomes more clear. Multiplication, because it deals with static quantities, can only measure the area of rectangles. Integrals let measurements curve and undulate as we go: we’ll add their contribution, regardless.
A series of multiplications becomes a series of integrals (called a triple integral). It’s beyond this primer, but your suspicion was correct: we can mimic the multiplications and integrate several times in a row.
Math, and specifically calculus, is the language of science because it describes relationships extremely well. When I see a formula with an integral or derivative, I mentally convert it to multiplication or division (remembering we can handle differently-sized elements).
6.3 Better Algebra
Algebra lets us start with one fact and systematically work out others. Imagine I want to know the area of an unknown square. I can’t measure the area, but I overheard someone saying it was 13.3 inches on a side.
| Algebra | Thinking Process |
| \( \textit{Area of square} = ? \) | The area of this square is unknown… |
| \( \sqrt{\textit{Area}} = 13.3 \) | …but I know the square root. |
| \( \left(\sqrt{\textit{Area}}\right)^2 = \left(13.3\right)^2 \) | Square both sides… |
| \( \textit{Area} = 176.89 \) | …and I can recreate the original area |
Remember learning that along with add/subtract/multiply/divide, we could take powers and roots? We added two new ways to transform an equation.
Well, calculus extends algebra with two more operations: integrals and derivatives. Now we can work out the area of a circle, algebra-style:
| Algebra + Calculus | Thinking Process |
| \( \textit{Area of circle} = ? \) | The area of a circle is unknown… |
| \( \dfrac{d}{dr} \textit{Area} = 2 \pi r \) | …but I know it splits into rings (along the radius) |
| \( \int \dfrac{d}{dr} \textit{Area} = \int 2 \pi r \) | Integrate both sides… |
| \( \textit{Area} = \pi r^2 \) | …and I can recreate the original area |
The abbreviated notation helps see the big picture. If the integrand only uses a single variable (as in \( 2 \pi r \)), we can assume we’re using \( dr \) from \( r=0 \) to \( r=r \). This helps us think of integrals and derivatives like squares and square roots: operations that cancel!
It’s pretty neat: “gluing together” and “splitting apart” should behave like opposites, right?
With our simpler notation, we can write \( \int \frac{d}{dr} \textit{Area} = \textit{Area} \) instead of the bulky \( \int_0^r \left( \frac{d}{dr} \textit{Area} \right) \ dr = \textit{Area} \).
6.4 Learning The Rules
With arithmetic, we learned special techniques for combining whole numbers, decimals, fractions, and roots/powers. Even though \( 3 + 9 = 12 \), we can’t assume \( \sqrt{3} + \sqrt{9} = \sqrt{12} \).
Similarly, we need to learn the rules for how integrals/derivatives work when added, multiplied, and so on. Yes, there are fancy rules for special categories (what to do with ex, natural log, sine, cosine, etc.), but I’m not concerned with that. Let’s get extremely comfortable with the basics. The fancy stuff can wait.