Chapter 5 Music From The Machine
In the previous lessons we’ve gradually sharpened our intuition:
- Appreciation: I think it’s possible to split up a circle to measure its area
- Natural Description: Split the circle into rings from the center outwards, like so:
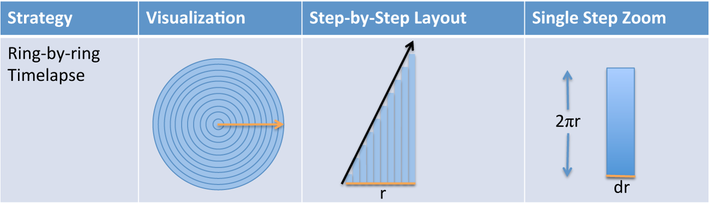
- Formal Description: integrate 2 * pi * r * dr from r=0 to r=r
- Performance: (Sigh) I guess I’ll have to start measuring the area…
Wait! Our formal description is precise enough that a computer can do the work for us:
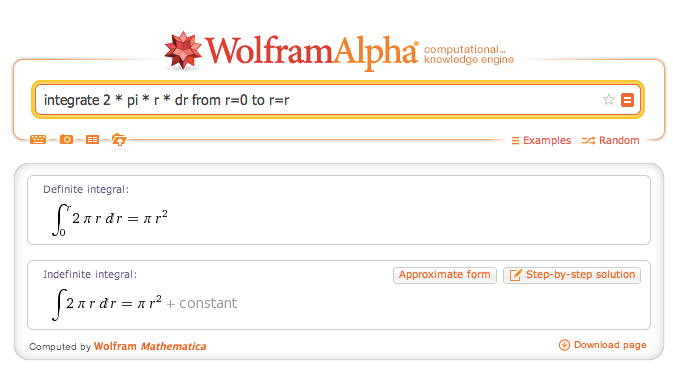
Whoa! We described our thoughts well enough that a computer did the legwork.
We didn’t need to manually unroll the rings, draw the triangle, and find the area (which isn’t overly tough in this case, but could have been). We saw what the steps would be, wrote them down, and fed them to a computer: boomshakalaka, we have the result. (Just worry about the “definite integral” portion for now.)
Now, how about derivatives, X-Raying a pattern into steps? Well, we can ask for that too:
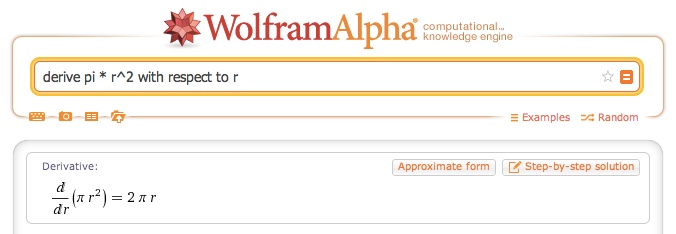
Similar to above, the computer X-Rayed the formula for area and split it step-by-step as it moved. The result is \( 2 \pi r \), the height of the ring at every position.
5.1 Seeing The Language In Action
Wolfram Alpha is an easy-to-use tool: the general format for calculus questions is
integrate [equation] from [variable=start] to [variable=end]take derivative of [equation] with respect to [variable]
That’s a little wordy. These shortcuts are closer to the math symbols:
\int [equation] dr— integrate equation (by default, assume we go from \( r=0 \) to \( r=r \), the max value)d/dr equation— take derivative of equation with respect to \( r \)- There’s shortcuts for exponents (
3⌃2 = 9), multiplication (3 * r), and roots (sqrt(9) = 3)
Now that we have the machine handy, let’s try a few of the results we’ve seen so far:
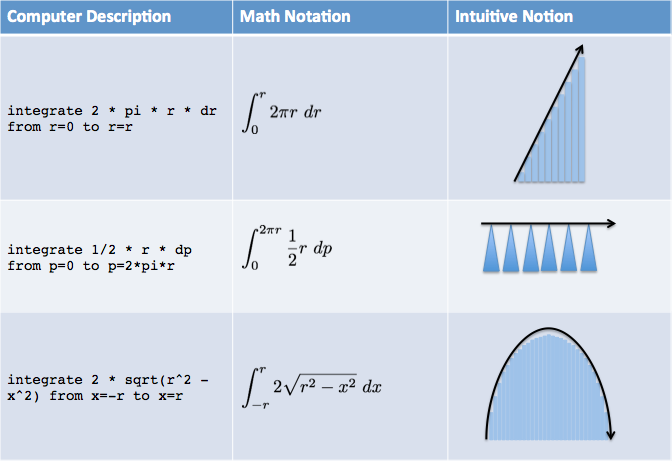
Click the formal description to see the computer crunch the numbers. As you might have expected, they all result in the familiar equation for area. A few notes:
- The size of the wedge is \( \frac{1}{2} \textit{base} \cdot \textit{height} \). The base is \( dp \) (the tiny section of perimeter) and the height is \( r \), the distance from the perimeter back to the center.
- The size of the board is tricky. In terms of x & y coordinates, we have \( x^2 + y^2 = r^2 \), by the Pythagorean Theorem:
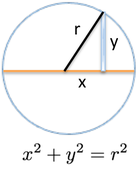
We solve for the height to get \( y = \sqrt{r^2 - x^2} \). We actually need 2 copies of height, because \( y \) is the positive distance above the axis, and the board extends above and below. The boards are harder to work with, and it’s not just you: Wolfram Alpha takes longer to compute this integral than the others!
The approach so far has been to immerse you in calculus thinking, and gradually introduce the notation. Some of it may be a whirl – which is completely expected. You’re sitting at a cafe, overhearing conversation in a foreign language.
Now that you have the sound in your head, we’ll begin to explore the details piece-by-piece.