Chapter 13 Finding Patterns In The Rules
We’ve uncovered the first few rules of calculus:
Instead of blasting through more rules, step back. Is there a pattern here?
13.1 Combining Perspectives
Imagine a business with interacting departments, or a machine with interconnected parts. What happens when we make a change? There’s a potential impact on each part.
If our business has 4 departments, and we make a policy change, there are 4 perspectives to consider. It sounds simple when written out: whenever a change happens, see what happens to each part!
No matter the specific interaction between parts F and G (addition, subtraction, multiplication, exponents…), we just have two perspectives to consider:
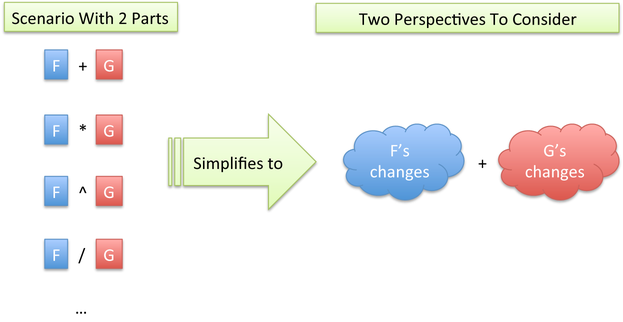
Aha! That’s why the rules for \( (f + g)' \) and \( (f \cdot g)' \) are two added perspectives. The derivative of \( \frac{1}{X} \) has a perspective because there’s just one “moving part”, x. (If you like, there is a contribution from “1” about the change it experiences: nothing. No matter how much you yell, 1 stays 1.)
The exact contribution from a perspective depends on the interaction:
- With addition, each part adds a direct change (\( df + dg \)).
- With multiplication, each part thinks it’ll add a rectangular strip (\( f \cdot dg + g \cdot df \)). (I’m using \( df \) instead of \( f' \) to help us think about the slice being added.)
You might forget the exact form of the multiplication rule. But you can think “The derivative of \( f \cdot g \) must be something with \( df \) + something with \( dg \).”
Let’s go further: what about the derivative of \( a \cdot b + c \)? You guessed it, 3 perspectives that should be added: something involving \( da \) plus something involving \( db \) plus something involving \( dc \).
We can predict the shape of derivatives for gnarly equations. What’s the derivative of:
Wow. I can’t rattle that off, but I can say it’ll be something involving 4 additions (\( dx \), \( dy \), \( du \) and \( dv \)). Guess the shape of a derivative, even if you don’t know the exact description.
Why does this work? Well, suppose we had a change that was influenced by both \( da \) and \( db \), such as \( 15 \cdot da \cdot db \) – that’d be our instrument interfering with itself!
Only direct changes on a single variable’s are counted (such as \( 3 da \) or \( 12 db \)), and “changes on changes’’ like \( 15 \cdot da \cdot db \) are ignored.
13.2 Dimensional Intuition
Remember that derivatives are a fancier form of division. What happens when we do a division like \( \frac{x^3}{x} \)? We divide volume by length, and get area (one dimension down).
What happens when we do \( \frac{d}{dx} x^3 \)? You might not know yet, but you can bet we’ll be dropping a dimension.
| Dimensions | Example | Description |
| 3 | \( x^3 \) | Volume (cubic growth) |
| 2 | \( x^2 \) | Area (square growth) |
| 1 | \( x \) | Length (linear growth) |
| 0 | \( c \) | Constant (no change) |
| -1 | \( \dfrac{1}{x} \) | Inverse length (“per length”) |
| -2 | \( \dfrac{1}{x^2} \) | Inverse area (“per area”) |
| -3 | \( \dfrac{1}{x^3} \) | Inverse volume (“per volume”) |
When we divide or take a derivative, we drop a dimension and hop down the table. Volume is built from area (slices \( dx \) thick), area is built from length (\( dx \) wide).
A constant value, like 3, has no dimension in the following sense: it never produces a set of slices. There will never be a jump to the next value. Once we have a constant value, we get “stuck” on the table because the 0 pattern always produces another 0 pattern (volume to area to lines to constant to zero to zero…).
We can have negative dimensions as well: “per length”, “per area”, “per volume”, etc. Derivatives still decrease the dimension, so when seeing \( \frac{1}{x} \), we know the derivative will resemble \( \frac{1}{x^2} \) as the dimension drops a level.
An important caveat: Calculus only cares about quantities, not their dimension. The equations will happily combine \( x \) and \( x^2 \), even though we know you can’t mix length with area. Units add a level of meaning from outside the equation, that help keep things organized and warn us if we’ve gone awry (if you differentiate area and get volume, you know something went wrong).
13.3 Thinking With Dimensions
You can think about the dimension of a derivative without digging into a specific formula. Imagine the following scenario:
- Take a string and wrap it tight around a quarter. Take another string and wrap it tight around the Earth.
- Lengthen both strings, adding more to the end, so there’s a 1-inch gap all the way around the quarter, and a 1-inch gap all the way around the Earth (like having a ring floating around Saturn).
- Quiz: Which scenario needed more extra string to create? Is it more string to put a 1-inch gap around the quarter, or a 1-inch gap around the Earth?
We can crunch through the formula, but think higher-level. Because circumference is a 1-d line, its reaction to change (the derivative) will be a constant. No matter the current size, the circumference will change the same amount with every push. So, the extra string needed is the same for both! (About 6.28 inches per inch of radius increase).
Now, suppose we were painting the sphere instead of putting a string around it. Ah, well, area is squared, therefore the derivative is a dimension lower (linear). If we have a 5-inch and 10-inch sphere, and make them 1-inch bigger each, the larger sphere will require double the extra paint.
13.4 Questions
Let’s think about the derivative of \( x^3 \), a growing cube.
1) What dimension should the derivative of \( x^3 \) have?
2) How many viewpoints should \( x^3 = x \cdot x \cdot x \) involve?
3) Have a guess for the derivative? Does it match with how you’d imagine a cube to grow?