Quick Insight: Easier Arithmetic With Calculus

Let's say you had to estimate 1 + 2 + 3 + 4 + 5 + 6 + 7 + ... + 100.

What would you do? Well, you could work out the exact formula:

$\displaystyle{\frac{(n + 1)(n)}{2}}$

and plug in n=100 to get 5050.

But we just want a rough answer. You have a list of numbers, they follow a simple pattern, and want a quick estimate. What to do?

The "easy" way (well, the Calculus way) is to realize 1 + 2 + 3 + 4 is about the same as $f(x) = x$. The first element is f(1) = 1, the second is f(2) = 2, and so on.

From here, we can take the integral:

$\displaystyle{ \int x = \frac{1}{2} x^2 }$

We usually see the integral as a formal, elegant operation, which artfully accumulates one function and returns another. Informally, we're squashing everything together in that bad mamma-jamma and seeing how much there is.

The result $\frac{1}{2} x^2$ should be pretty close to what we want.

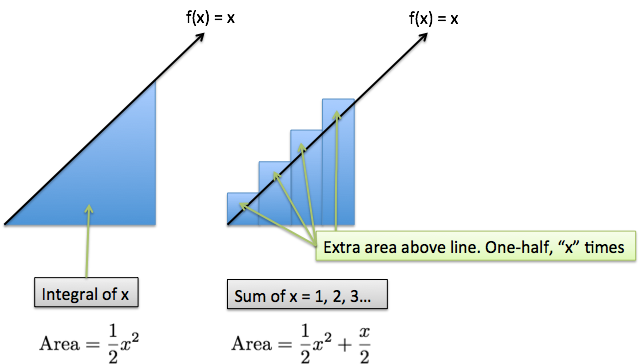
The exact total is our staircase-like pattern, which accumulates to 5050.

The approximate answer is the area of that triangle, $\frac{1}{2} base * height = \frac{1}{2} 100 * 100 = 5000$. The difference is because of the corners in the staircase which overhang. $\frac{x}{2}$ is one-half, x times (the size of overhang (1/2) times the number of pieces (x)).

The net result is using a smooth, easy-to-measure shape to approximate a jagged, tedious-to-measure one. (This is a bit of Calculus inception, since we usually use rectangles to approximate smooth shapes.)

More Estimates

This tactic works for other sequences:

What's the sum of the first 10 square numbers? 1 + 4 + 9 + 16 + 25 + ... + 100 = ?

Hrm. The formula is probably tricky to work out. But without our Calculus-infused Arithmetic, a quick guess would be:

$\displaystyle{\int x^2 = \frac{1}{3} x^3}$

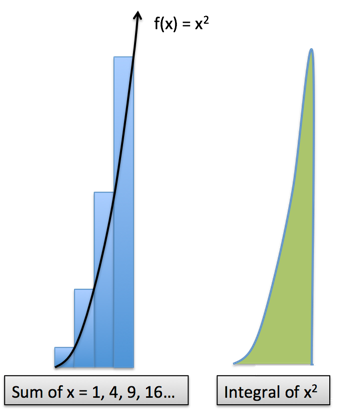
Our first hunch should be "one third of 10^3" or 333. But as we saw before, there's an "overhang" that we missed. Let's call it 10%, for an estimate of 330 + 10% ~ 370.

The exact answer is 385. Not bad! The actual formula is:

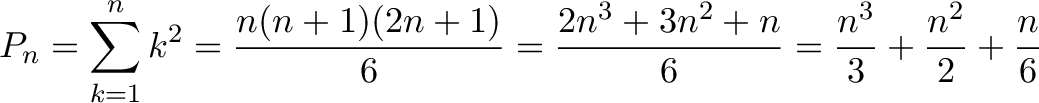
$\displaystyle{P_{n}=\sum _{k=1}^{n}k^{2}={\frac {n(n+1)(2n+1)}{6}}={\frac {2n^{3}+3n^{2}+n}{6}}={\frac {n^{3}}{3}}+{\frac {n^{2}}{2}}+{\frac {n}{6}} }$

I'd say $\frac{x^3}{3}$ isn't bad for a few seconds of work.

Data doubles every year. What does lifetime usage look like?

The integral (squashed-together total) of an exponential is an exponential. In Calculus terms,

$\displaystyle{\int e^x = e^x}$

The key insight is that all exponential growth is just a variation of $e^x$. If $e^x$ accumulates exponentially, so will $2^x$.

So the total usage to date will also follow an exponential pattern, doubling every year also. Contrast this with a usage pattern of "1 + 2 + 3 + 4 ..." -- we grow linearly ($f(x) = x$), but total usage accumulates quadratically ($\frac{1}{2}x^2$).

My goal is to incorporate math thinking into everyday scenarios. We start with an arithmetic question, convert it to a geometry puzzle (how big is the staircase?), and then use calculus to approximate it.

I know a concept is clicking when I can switch between a few styles of thought. Imagine the problem as a script: how would Spielberg, Tarantino, or Scorsese direct it? Each field takes a different look. (To learn how to think with Calculus, check out the Calculus Guide.)

Happy math.

Quick Insight: Easier Arithmetic With Calculus

More Estimates

Other Posts In This Series

Join 450k Monthly Readers