Analogy: The Calculus Camera

Imagine you're a photographer. You come across a beautiful, reflective object: a metal sphere, a calm lake, a mirrored room. Seems like a good photo op, right?

Sure, except your photos come out like this:

(An old-timey selfie. Source.)

The dilemma: You need a camera for the photo, but don't want the camera in the photo. The instrument shouldn't appear inside the subject. (Hubert, you're leaving scalpels in the patient again.)

So, we need an isolated photo of a shiny object. What can we do?

Shrink it down: Make the camera as small as possible. Microscopic, a fleck of dust. But even that speck will show up on the sphere. Take the photo, and fix the blemish with our best guess given the surrounding pixels.
Go invisible: Make the camera unobservable to the subject: make it from perfectly transparent glass, or actively camouflage with your surroundings (like an octopus). The camera is there, looking at the subject, but the subject cannot notice it.

In Calculus, a function like $f(x) = x^2$ is our subject. Limits (shrinking) and infinitesimals (invisibility) are how we take photos without our reflection getting in the way.

Taking a Photo of a Function

Consider a function like $f(x) = 2x + 3$. If I take a photo with my camera, I get:

Before: $f(x) = 2x + 3$
After: $f(x + \text{camera}) = 2(x + \text{camera}) + 3 = 2x + 3 + 2\text{camera}$

We have the original function, and put the camera into the scene. The result is the original function ($2x + 3$) and the camera observing "2". That is, the camera thinks "2" is how much the function has changed. (And yes, $\frac{d}{dx} 2x + 3 = 2$.)

Ok. Now take a function like $f(x) = x^2$. Again, let's put the camera into the scene to observe changes:

Before: $f(x) = x^2$
After: $f(x + \text{camera}) = (x + \text{camera})^2 = x^2 + 2x \cdot \text{camera} + \text{camera}^2$

Hrm. The camera is directly observing some changes ($2x \cdot \text{camera}$) but there's another $\text{camera}^2$ term: the camera is observing its own reflection! The term $\text{camera}^2$ only exists because we have a camera in the first place. It's an illusion.

What's the fix?

List all the changes the camera sees:

$\begin{aligned} f(x + \text{camera}) - f(x) &= [x^2 + 2x \cdot \text{camera} + \text{camera}^2] - [x^2] \\ &= 2x \cdot \text{camera} + \text{camera}^2 \end{aligned}$
Figure out what the camera directly observed. We divide to see what was "attached" to the camera:

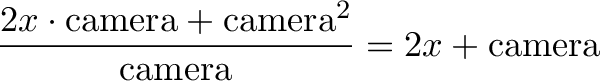
$\displaystyle{\frac{2x \cdot \text{camera} + \text{camera}^2}{\text{camera}} = 2x + \text{camera}}$
Remove "reflections" where the camera saw itself:

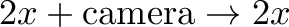
$\displaystyle{2x + \text{camera} \rightarrow 2x}$

From a technical perspective, the last step happens by shrinking the camera to zero (limits) or letting the camera be invisible (infinitesimals).

Neat, eh? We're reframing the process of finding the derivative: make a change, see what the direct effects are, remove the artifacts. The concept of "what the camera directly sees" and the camera's "reflection" help settle my mind about throwing away terms that appear to be there.

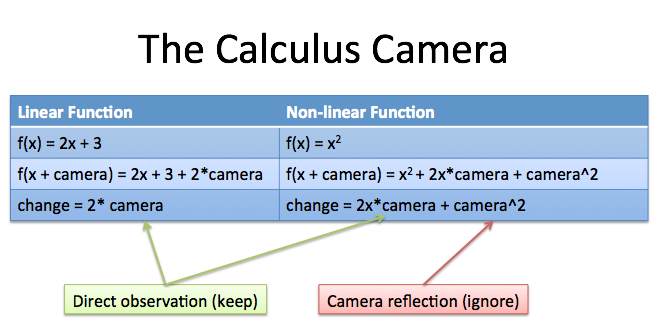
In math, we have fancy terms like linear and non-linear functions. We can think in terms of "shiny" or "dull" functions.

Linear functions are dull because they only have terms like $x$ or constant values -- the camera can attach directly, and there's no reflection. Non-linear functions have self-interactions (like $x^2$) which means the camera has a chance to see itself. Reflections need to be removed.

With multiple subjects [$f(x)$, $g(x)$] or multiple cameras (for the x, y and z axis) we get cross terms like $df \cdot dg$ or $dx \cdot dy$. The goal is the same: remove unnecessary self- and cross-reflections from the final result. Show what the camera directly sees.

A few related blog posts on limits:

The role of dx

Regular calculus books use $dx$ as the camera to detect change. The goal is to introduce a change ($dx$), then get the difference ($f(x + dx) - f(x)$).

This difference (for example, $2x \cdot dx + dx^2$) isolates the changes that $dx$ is directly responsible for ("sees"). We can then divide by $dx$ to get the change as a rate (how much we got out for how much we put in).

The concern is the same: the change $dx$ may have reflections ($dx^2$) that need to be removed.

Real-World Application: The Hawthorne Effect

The Hawthorne Effect is where people behave differently when being studied. The study itself is appearing in the results.

If you ask people to enter a study about their eating, exercise, reading, or sleeping habits, those behaviors will change. (Gotta look good for the camera! Where are those Greek philosophers I'd always meant to read?)

Math gives us a few suggestions:

Shrink the effect: Make the study as non-intrusive as possible (like an iPhone passively monitoring your steps). Even then, figure out how much the results are skewed and adjust for this. (You left your phone on the washing machine again, you sly dog.)
Make the observations invisible: Imagine you don't know when the study is going to start. "Sometime in the next 20 years we'll silently observe your grocery shopping habits. Sign here." Hrm. You won't change your behavior for 20 years "just in case", so you'll just be you.

Think math only applies to equations? Hah. Only if we don't internalize the underlying concept.

Happy math.

Analogy: The Calculus Camera

Taking a Photo of a Function

The role of dx

Real-World Application: The Hawthorne Effect

Other Posts In This Series

Join 450k Monthly Readers