How to Add 1 through 100 using Calculus

Earlier we saw a few ways to add a set of numbers (1 to 10).

And the formula we found was:

$\displaystyle{\text{Sum from 1 to n} = \frac{n(n+1)}{2}}$

$\displaystyle{\text{Sum from 1 to 100} = \frac{100(100+1)}{2} = (50)(101) = 5050}$

It seems that regular arithmetic, algebra, geometry, or even statistics could help work out the equation.

But how about Calculus? Is this bringing a nuclear missile to a gun fight?

Let's find out.

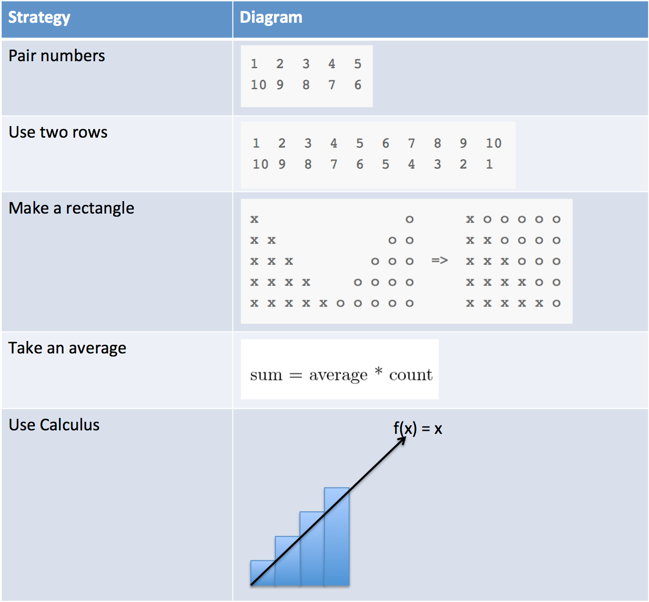
The sequence to add (1 2 3 4 5 6 7 8 9 10...) looks a lot like $f(x) = x$. At every position on the x-axis, we put in a number and get the same one out.

Intuitively, the integral is "repeatedly adding a bunch of stuff" -- it seems like we could put it to work. From the rules of Calculus (or using Wolfram Alpha) we get this:

$\displaystyle{ \int x = \frac{1}{2} x^2 }$

Intuitively: Add up things following the $f(x) = x$ pattern and you end up with $\frac{1}{2} x^2$.

Well, let's see: the actual sum from 1 to 100 is 5050. But using the Calculus equation we get:

$\displaystyle{ \frac{1}{2} x^2 = \frac{1}{2}100^2 = \frac{10,000}{2} = 5000 }$

Uh oh: there's a difference. What's going on?

Calculus works with continuous patterns, and we used a discrete one.

Here's what's happening:

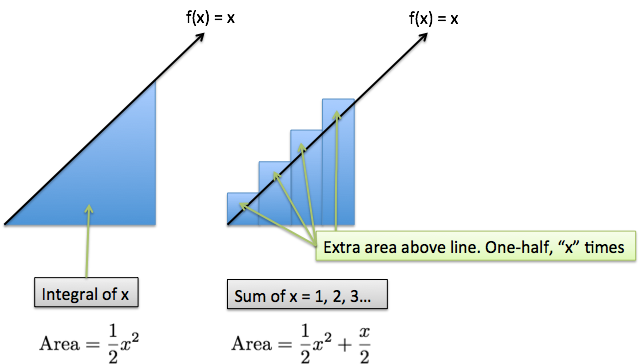
Calculus was built to measure smoothly changing functions, like a line, parabola, circle, etc. The pattern we have is a jumpy staircase (going from 1 to 2 without ever passing through 1.5, or 1.1, or 1.0001). In math class, books harp on analyzing whether a function is "continuous", aka changes smoothly enough for Calculus to work.

So when a pattern changes smoothly, Calculus works great. If a pattern changes suddenly, Calculus can only give an approximate answer. So what's the plan?

Use Calculus where possible, on the smooth part, and adjust for errors in the jumpy part.

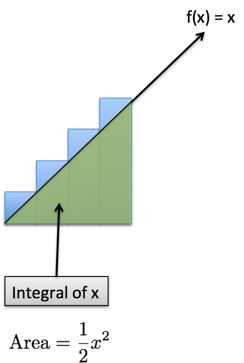
The area under the line is the integral. We a bunch of triangles above the line we need to include.

How many of them? 1 for each item (x)
How big are they? They're half a of a 1x1 square, so they have area 1/2.
What's the total area to add back in? $x \frac{1}{2} = \frac{x}{2}$

So our final formula should be

$\displaystyle{\text{Integral} + \text{Adjustment} = \frac{1}{2} x^2 + \frac{x}{2}}$

Aha! Learning Calculus doesn't mean we hunt around for Official Calculus Problems.

Nope. Take your scenario (adding 1 to 100) and realize what Calculus brings to the table: finding patterns in smoothly changing functions. Use Calculus on the smooth parts and adjust (or ignore) the other parts.

(Ironically, Calculus works by making jumpy approximations for smooth functions, and is in fact "jumpy" under the hood. If you are planning on working with jumpy patterns, use Discrete Calculus.)

Example: Adding the first n squares

Let's take this further: what's your guess for the sum of the first 100 square numbers?

$\displaystyle{1^2 + 2^2 + 3^2 + 4^2 + ... + 100^2}$

Hrm. Getting the exact formula is tricky. But maybe we don't need the exact count, just an estimate.

With Calculus, we'd say: The pattern isn't continuous, but it looks like $f(x) = x^2$. Let's integrate x^2 from 0 to 100.

$\displaystyle{ \int x^2 = \frac{1}{3} x^3 }$

The indefinite integral is $\frac{1}{3} x^3 $, the running total for how much we have. From 0 to 100 it would be

$\displaystyle{ \frac{1}{3}100^3 = \frac{1,000,000}{3} \sim 333,333 }$

That's our guess, without a calculator. And the actual answer? 338350.

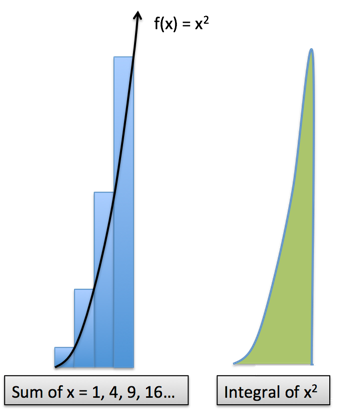
How close were we? 99.9%. Not bad for something we worked out by hand in a minute!

Truly internalizing Calculus means it helps other elements of your math understanding, even regular addition problems.

Happy math.

PS. To keep building your intuition, check out the Calculus Guide.

How to Add 1 through 100 using Calculus

Example: Adding the first n squares

Other Posts In This Series

Join 450k Monthly Readers