A Calculus Analogy: Integrals as Multiplication

Integrals are often described as finding the area under a curve. This description is too narrow: it's like saying multiplication exists to find the area of rectangles. Finding area is a useful application, but not the purpose of multiplication.

Key insight: Integrals help us combine numbers when multiplication can't.

I wish I had a minute with myself in high school calculus:

"Psst! Integrals let us 'multiply' changing numbers. We're used to "3 x 4 = 12", but what if one quantity is changing? We can't multiply changing numbers, so we integrate.

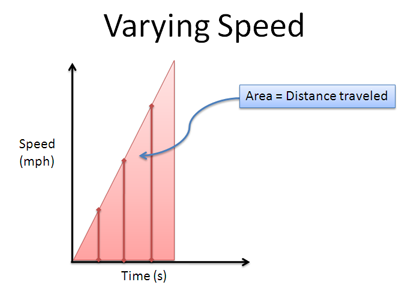
You'll hear a lot of talk about area -- area is just one way to visualize multiplication. The key isn't the area, it's the idea of combining quantities into a new result. We can integrate ("multiply") length and width to get plain old area, sure. But we can integrate speed and time to get distance, or length, width and height to get volume.

When we want to use regular multiplication, but can't, we bring out the big guns and integrate. Area is just a visualization technique, don't get too caught up in it. Now go learn calculus!"

That's my aha moment: integration is a "better multiplication" that works on things that change. Let's learn to see integrals in this light.

Understanding Multiplication

Our understanding of multiplication changed over time:

With integers (3 x 4), multiplication is repeated addition
With real numbers (3.12 x $\sqrt{2}$), multiplication is scaling
With negative numbers (-2.3 * 4.3), multiplication is flipping and scaling
With complex numbers (3 * 3i), multiplication is rotating and scaling

We're evolving towards a general notion of "applying" one number to another, and the properties we apply (repeated counting, scaling, flipping or rotating) can vary. Integration is another step along this path.

Understanding Area

Area is a nuanced topic. For today, let's see area as a visual representation of of multiplication:

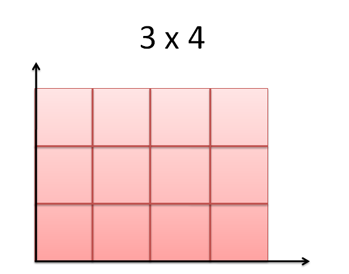
With each count on a different axis, we can "apply them" (3 applied to 4) and get a result (12 square units). The properties of each input (length and length) were transferred to the result (square units).

Simple, right? Well, it gets tricky. Multiplication can result in "negative area" (3 x (-4) = -12), which doesn't exist.

We understand the graph is a representation of multiplication, and use the analogy as it serves us. If everyone were blind and we had no diagrams, we could still multiply just fine. Area is just an interpretation.

Multiplication Piece By Piece

Now let's multiply 3 x 4.5:

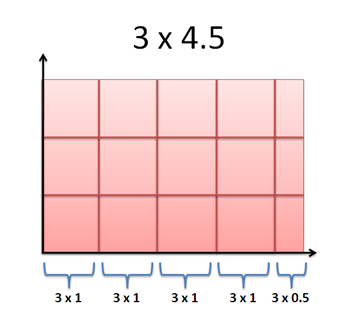
What's happening? Well, 4.5 isn't a count, but we can use a "piece by piece" operation. If 3x4 = 3 + 3 + 3 + 3, then

3 x 4.5 = 3 + 3 + 3 + 3 + 3x0.5 = 3 + 3 + 3 + 3 + 1.5 = 13.5

We're taking 3 (the value) 4.5 times. That is, we combined 3 with 4 whole segments (3 x 4 = 12) and one partial segment (3 x 0.5 = 1.5).

We're so used to multiplication that we forget how well it works. We can break a number into units (whole and partial), multiply each piece, and add up the results. Notice how we dealt with a fractional part? This is the beginning of integration.

The Problem With Numbers

Numbers don't always stay still for us to tally up. Scenarios like "You drive 30mph for 3 hours" are for convenience, not realism.

Formulas like "distance = speed * time" just mask the problem; we still need to plug in static numbers and multiply. So how do we find the distance we went when our speed is changing over time?

Describing Change

Our first challenge is describing a changing number. We can't just say "My speed changed from 0 to 30mph". It's not specific enough: how fast is it changing? Is it smooth?

Now let's get specific: every second, I'm going twice that in mph. At 1 second, I'm going 2mph. At 2 seconds, 4mph. 3 seconds is 6mph, and so on:

Now this is a good description, detailed enough to know my speed at any moment. The formal description is "speed is a function of time", and means we can plug in any time (t) and find our speed at that moment ("2t" mph).

(This doesn't say why speed and time are related. I could be speeding up because of gravity, or a llama pulling me. We're just saying that as time changes, our speed does too.)

So, our multiplication of "distance = speed * time" is perhaps better written:

$\displaystyle{\text{distance} = \text{speed}(t) \cdot t}$

where speed(t) is the speed at any instant. In our case, speed(t) = 2t, so we write:

$\displaystyle{\text{distance} = 2t \cdot t}$

But this equation still looks weird! "t" still looks like a single instant we need to pick (such as t=3 seconds), which means speed(t) will take on a single value (6mph). That's no good.

With regular multiplication, we can take one speed and assume it holds for the entire rectangle. But a changing speed requires us to combine speed and time piece-by-piece (second-by-second). After all, each instant could be different.

This is a big perspective shift:

Regular multiplication (rectangular): Take the amount of distance moved in one second, assume it's the same for all seconds, and "scale it up".
Integration (piece-by-piece): See time as a series of instants, each with its own speed. Add up the distance moved on a second-by-second basis.

We see that regular multiplication is a special case of integration, when the quantities aren't changing.

How large is a "piece"?

How large is a "piece" when going piece by piece? A second? A millisecond? A nanosecond?

Quick answer: Small enough where the value looks the same for the entire duration. We don't need perfect precision.

The longer answer: Concepts like limits were invented to help us do piecewise multiplication. While useful, they are a solution to a problem and can distract from the insight of "combining things". It bothers me that limits are introduced in the very start of calculus, before we understand the problem they were created to address (like showing someone a seatbelt before they've even seen a car). They're a useful idea, sure, but Newton seemed to understand calculus pretty well without them.

What about the start and end?

Let's say we're looking at an interval from 3 seconds to 4 seconds.

The speed at the start (3x2 = 6mph) is different from the speed at the end (4x2 = 8mph). So what value do we use when doing "speed * time"?

The answer is that we break our pieces into small enough chunks (3.00000 to 3.00001 seconds) until the difference in speed from the start and end of the interval doesn't matter to us. Again, this is a longer discussion, but "trust me" that there's a time period which makes the difference meaningless.

On a graph, imagine each interval as a single point on the line. You can draw a straight line up to each speed, and your "area" is a collection of lines which measure the multiplication.

Where is the "piece" and what is its value?

Separating a piece from its value was a struggle for me.

A "piece" is the interval we're considering (1 second, 1 millisecond, 1 nanosecond). The "position" is where that second, millisecond, or nanosecond interval begins. The value is our speed at that position.

For example, consider the interval 3.0 to 4.0 seconds:

"Width" of the piece of time is 1.0 seconds
The position (starting time) is 3.0
The value (speed(t)) is speed(3.0) = 6.0mph

Again, calculus lets us shrink down the interval until we can't tell the difference in speed from the beginning and end of the interval. Keep your eye on the bigger picture: we are multiplying a collection of pieces.

Understanding Integral Notation

We have a decent idea of "piecewise multiplication" but can't really express it. "Distance = speed(t) * t" still looks like a regular equation, where t and speed(t) take on a single value.

In calculus, we write the relationship like this:

$\displaystyle{\text{distance} = \int \text{speed}(t) \ dt}$

The integral sign (s-shaped curve) means we're multiplying things piece-by-piece and adding them together.
dt represents the particular "piece" of time we're considering. This is called "delta t", and is not "d times t".
t represents the position of dt (if dt is the span from 3.0-4.0, t is 3.0).
speed(t) represents the value we're multiplying by (speed(3.0) = 6.0))

I have a few gripes with this notation:

The way the letters are used is confusing. "dt" looks like "d times t" in contrast with every equation you've seen previously.
We write speed(t) * dt, instead of speed(t_dt) * dt. The latter makes it clear we are examining "t" at our particular piece "dt", and not some global "t"
You'll often see $\int speed(t)$, with an implicit dt. This makes it easy to forget we're doing a piece-by-piece multiplication of two elements.

It's too late to change how integrals are written. Just remember the higher-level concept of 'multiplying' something that changes.

Reading In Your Head

When I see

$\displaystyle{\text{distance} = \int \text{speed}(t) \ dt}$

I think "Distance equals speed times time" (reading the left-hand side first) or "combine speed and time to get distance" (reading the right-hand side first).

I mentally translate "speed(t)" into speed and "dt" into time and it becomes a multiplication, remembering that speed is allowed to change. Abstracting integration like this helps me focus on what's happening ("We're combining speed and time to get distance!") instead of the details of the operation.

Bonus: Follow-up Ideas

Integrals are a deep idea, just like multiplication. You might have some follow-up questions based on this analogy:

If integrals multiply changing quantities, is there something to divide them? (Yes -- derivatives)
And do integrals (multiplication) and derivatives (division) cancel? (Yes, with some caveats).
Can we re-arrange equations from "distance = speed * time" to "speed = distance/time"? (Yes.)
Can we combine several things that change? (Yes -- it's called multiple integration)
Does the order we combine several things matter? (Usually not)

Once you see integrals as "better multiplication", you're on the lookout for concepts like "better division", "repeated integration" and so on. Sticking with "area under the curve" makes these topics seem disconnected. (To the math nerds, seeing "area under the curve" and "slope" as inverses asks a lot of a student).

Reading integrals

Integrals have many uses. One is to explain that two things are "multiplied" together to produce a result.

Here's how to express the area of a circle:

$\displaystyle{\text{Area} = \int \text{Circumference}(r) \cdot dr = \int 2 \pi r \cdot dr = \pi \cdot r^2}$

We'd love to take the area of a circle with multiplication. But we can't -- the height changes as we go along. If we "unroll" the circle, we can see the area contributed by each portion of radius is "radius * circumference". We can write this relationship using the integral above. (See the introduction to calculus for more details).

And here's the integral expressing the idea "mass = density * volume":

$\displaystyle{\text{mass} = \int_V \rho(\vec{r})dv}$

What's it saying? Rho: $\rho$ is the density function -- telling us how dense a material is at a certain position, r. dv is the bit of volume we're looking at. So we multiply a little piece of volume (dv) by the density at that position $\rho(r)$ and add them all up to get mass.

We'd love to multiply density and volume, but if density changes, we need to integrate. The subscript V means is a shortcut for "volume integral", which is really a triple integral for length, width, and height! The integral involves four "multiplications": 3 to find volume, and another to multiply by density.

We might not solve these equations, but we can understand what they're expressing.

Onward an upward

Today's goal isn't to rigorously understand calculus. It's to expand our mental model, and realize there's another way to combine things: we can add, subtract, multiply, divide... and integrate.

See integrals as a better way to multiply: calculus will become easier, and you'll anticipate concepts like multiple integrals and the derivative. Happy math.

(PS. Zach at SMBC put himself into a... uh... comic about this intuition.)