Learning Calculus: Overcoming Our Artificial Need for Precision

by
Like it? Try the ebook

Accepting that numbers can do strange, new things is one of the toughest parts of math:

  • There’s numbers between the numbers we count with? (Yes — decimals)
  • There’s a number for nothing at all? (Sure — zero)
  • The number line is two dimensional? (You bet — imaginary numbers)

Calculus is a beautiful subject, but challenges some long-held assumptions:

  • Numbers don’t have to be perfectly accurate?
  • Numbers aren’t all the same size (i.e. 1 times some number)?

Today’s post introduces a new way to think about accuracy and infinitely small numbers. This is not a rigorous course on analysis — it’s my way of grappling with the ideas behind Calculus.

Counting Numbers vs. Measurement Numbers

Not every number is the same. We don’t often consider the difference between the “counting numbers” (1, 2, 3…) and the “measuring numbers” like 2.58, pi, sqrt(2).

Our first math problems involve counting: we have 5 apples and remove 3, or buy 3 books at $10 each. These numbers change in increments of 1, and everything is nice and simple.

We later learn about fractions and decimals, and things get weird:

  • What’s the smallest fraction? (1/10? 1/100? 1/1000?)
  • What’s the next decimal after 1.0? 1.1? 1.001?

It gets worse. Numbers like sqrt(2) and \displaystyle{\pi} go on forever, without a pattern. Numbers “in the real world” have all sorts of complexity not found in our nice, chunky counting numbers.

We’re hit with a realization: we have limited accuracy for quantities that are measured, not counted.

What do I mean? Find the circumference of a circle of radius 3. Oh, that’s easy; plug r=3 into circumference = 2 * pi * r and get 6*pi. Tada!

That’s cute, but you didn’t answer my question — what number is it?

You may pout, open your calculator and say it’s “18.8495…”. But that doesn’t answer my question either: What, exactly, is the circumference?

We don’t know! Pi continues forever and though we know a trillion digits, there’s infinitely more. Even if we knew what pi was, where would we write it down? We really don’t know the exact circumference of anything!

But hush hush — we’ve hidden this uncertainty behind a symbol, \displaystyle{\pi}. When you see \displaystyle{\pi} in an equation it means “Hey buddy, you know that number, the one related to circles? When it’s time to make a calculation, just use the closest approximation that works for you.”

Again, that’s what the symbol means — we don’t know the real number, so use your best guess. By the way, e and \displaystyle{\sqrt{2}}) have the same caveat.

40 digits of pi should be enough for anyone

We think uncertainty is chaos: how can you build a machine unless you know the exact sizes of its parts?

But as it turns out, the “closest approximation of pi that works for us” tends to be surprisingly small. Yes, we’ve computed pi to billions of digits but we only need about 40 for any practical application.

Why? Consider this:

Dividing it out, it takes about 1e38 (1e27 / 1e-11) atoms to span the universe. So, around 40 digits of pi would be enough for an exact count of atoms needed to surround the universe. Were you planning on building something larger than the universe and precise to an atomic level? (If so, where would you put it?)

And that’s just 40 digits of precision; 80 digits covers us in case there’s a mini-universe inside each of our atoms, and 120 digits in case there’s another mini-universe inside of that one.

The point is our instruments have limited precision, and there’s a point where extra detail just doesn’t matter. Pi could become a sudoku puzzle after the 1000th digit and our machines would work just fine.

But I need exact numbers!

Accepting uncertainty is hard: what is math if not accurate and precise? I thought the same, but started noticing how often we’re tricked in the real world:

  • Our brains are fooled into thinking 24 images per second is the same as fluid motion.
  • Every digital photo (and printed ones, too!) are made from tiny pixels. Pictures seem smooth image until you zoom in:

pixelation

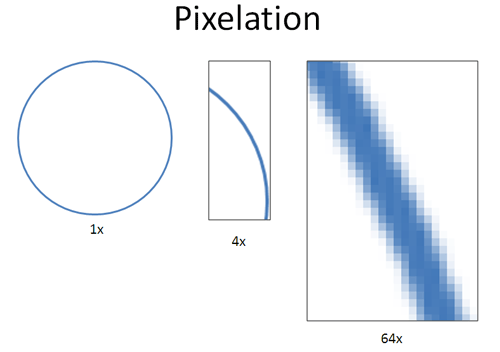
The big secret is that every digital photo is pixelated: we only call it pixelated when we happen to notice the pixels. Otherwise, when the squares are tiny enough we’re fooled into thinking we have a smooth picture. But it’s just smooth for human eyes.

This happens to mechanical devices also. At the atomic level, there limits on measurement certainty that restrict how well we can know a particle’s speed and location. Some modern theories suggest a quantized universe — we might be living on a grid!

Here’s the point: approximations are a part of Nature, yet everything works out. Why? We only need to be accurate within our scale. Uncertainty at the atomic level doesn’t matter when you’re dealing with human-sized objects.

Every number has a scale

The twist is realizing that even numbers have a scale. Just like humans can’t directly observe atoms, some numbers can’t directly interact with “infinitesimals” or infinitely small numbers (in the line of 1/2, 1/3… 1/infinity).

But infinitesimals and atoms aren’t zero. Put a single atom and on your bathroom scale, and the scale still reads nothing. Infinitesimals behave the same way: in our world of large numbers, 1 + infinitesimal looks just like 1 to us.

Now here’s the tricky part: A billion, trillion, quadrillion, kajillion infinitesimals is still undetectable! Yes, I know, in the real world if we keep piling atoms onto our scale, eventually it will register as some weight. But not so with infinitesimals. They’re on a different plane entirely — any finite amount of them will simply not be detectable. And last time I checked, we humans can only do things in finite amounts.

Let’s think about infinity for a minute, intuitively:

  • Infinity “exists” but is not reachable by our standard math. No amount of addition or multiplication will take you there — we need an infinite amount of addition to make infinity (circular, right?). Similarly, no finite amount of division will create an infinitesimal.
  • Infinity and infinitesimals require new rules of arithmetic, just like fractions and complex numbers changed the way we do math. We’ll get into this more later.

It’s strange to think about numbers that appear to be zero at our scale, but aren’t. There’s a difference between “true” zero and a measured zero. I don’t fully grasp infinitesimals, but I’m willing to explore them since they make Calculus easier to understand.

Just remember that negative numbers were considered “absurd” even in the 1700s, but imagine doing algebra without them.

Life Lessons

Math can often apply to the real world. In this case, it’s the realization that accuracy exists on different levels, and perfect accuracy isn’t needed. We only need 40 digits of pi for our engineering calculations!

When doing market research, would knowing 80% vs 83.45% really change your business decision? The former is 100x less precise and probably 10x easier to get, yet contains almost the same decision-making information.

In science, there’s an idea of significant figures, which help portray uncertainty in our measurements. We’re so used to contrived math problems (“Suzy is driving at 50mph for 3 hours”) that we forget the real world isn’t that clean. Information can be useful even if it’s not perfectly precise.

Math Lessons

Calculus was first developed using infinitesimals, which were abandoned for techniques with more “rigor”. Only in the 1960′s (not that long ago!) were the original methods shown to be justifiable, but it was too late — many calculus explanations are separate from the original insights.

Again, my goal is to understand the ideas behind Calculus, not simply rework the mechanics of its proofs. The first brain-bending ideas are that perfect accuracy isn’t necessary and that numbers can exist on different scales.

There’s a new type of number out there: the infinitesimal. In future posts we’ll see how to use them. Happy math.

Share what worked: Aha moments & FAQ

Let's create a living reference for how best to understand this topic.

57 thoughts on “Learning Calculus: Overcoming Our Artificial Need for Precision”

  1. Hi! Kalid

    I have been following this Blog for some time. Really appreciate the time and effort you are putting into this to help us better understand the concepts and create “Aha moments”

    I’m learning and getting a lot of interesting insights from this blog.

    Thanks!
    -Mahesh
    Celebrating Life…

  3. @Mahesh: Thanks for the note! Glad you’re enjoying the site, it’s been a lot of fun to make so far. Always happy to have you drop in.

    @Calin: Glad you found it useful! I’ve always been befuddled by the inner workings of Calculus, but I think infinitesimals can make it a lot more clear.

  10. Hi Kalid, nice post, as always. I like the title “Overcoming the Artificial Need for Precision.” I’d like to add one more point to that, not about Math really.

    I believe that I should try for precision in order to get to the closest possible approximation. It’s like striving for the perfect software with no bugs knowing that there is no software that has “zer0″ bugs. Deadlines and other external forces can resist (or end) our quest for perfection. OK, What am I trying to say here? Oh yes, this is what. Even if we strive for perfection, time will stop us and it’s not that bad to strive for perfection in that time frame.

    And BTW, I liked that pixelation example very much. Thanks for post.

  11. Hi Srikanth, thanks for the comment. I agree — we should always strive for the maximum precision possible, while realizing that our precision is limited (not infinite).

  12. Hi!

    I welcome your slow cooking approach to the introduction of calculus which is ultimately going to be delicious.

    Occasionally, I suggest, you throw a A4 piece of paper to non-calculus mortals and ask them to come up with largest volume of rectangular box in conventional way and show us , it can be done with one stroke through calculus in your unique way.

    Is it a long way?

    Regards,

    T.Gopalan

  13. Hi T.Gopalan, thanks for the comment & kind words. I’m not sure I understand the question — were you thinking of ways to make the biggest box possible given some constraints? Or a box with infinity on each side? :) .

  16. Hi! Kalid,
    What I mean is the A4 size paper has constraint
    dimension of 210 x 297 mm. I hope I am making myself clear.
    Thanks for your response,

    T.Gopalan

  18. Kalid,

    My son was given the problem that T.Gopalan mentions – take a sheet of paper, cut equal-sized squares out of each corner, and fold the sides up to create a box (with no lid). His assignment was to find the size of the squares that would make a box with the largest volume, through trial and error, to the nearest tenth of a cm. I told him that his teacher would probably relate this to calculus and show how to find the exact answer., but his teacher never did – an opportunity missed!

  19. Interesting perspective anh. I do like you approach to explaining precision. But one thing baffles me: how precise in approximations should we get when we whip out that calculator to crunch numbers when dealing with… say chemistry math? I remember struggling to decide to what decimal point we should use for calculations, how “precise” we should be, back in college. Any suggestions?

  20. @Bruce, T.Gopalan: Ah, thanks for the clarification! Yes, that’s an interesting problem that calculus can help solve — I’ll keep it in mind as an example for upcoming articles!

    @VT: Thanks Em, great question — it’s been a while since I’ve done any chemistry, let’s see if I can remember :) .

    In my head, I think you can only be as accurate as the “weakest” link in a chain. For example, someone said “Dinosaurs died 65 million years ago” in 1950, it doesn’t mean they died 65 million + 58 years ago :) . The 58 years that have passed don’t even register, since 65 million is a very rough number (only 2 digits of accuracy) but 65,000,058 is a pretty accurate number (8 digits).

    Intuitively, I look at how many digits “haven’t been rounded” so if you see 3.1 kg, it has 2 digits of accuracy (and 3kg has 1 digit of accuracy). When doing calculations, you need to keep that same number of digits that “haven’t been rounded” so you don’t give the impression of super-precise measurements. So after you do all the intermediate math, you round it back to the level of accuracy you started with. Hopefully this helps!

  21. @Prateek: Thanks!

    @Quan: Appreciate the comment. Wow, 60 digits of pi… building a ring around the universe? :)

    @biophonc: Glad you enjoyed it.

  22. Nicely written. Concise, correct and clear. Always good to see old concepts reiterated in a helpful way.

    Good job, I enjoyed reading it.

  24. I can’t really say much, except that I really enjoyed reading that :) Nice work!

    Only nitpick is that 1e27 / 1e-11 = 1e38 not 1e37 ;)

  25. You say that “It doesn’t matter how many infinitesimals we add — we’ll never detect them!” Calculus is in business of dealing with things to small to detect. But the most powerful part of calculus is the fact that you CAN add up enough “infinitesimals” to find the area of an irregular shape, or to find the rate of change of a quantity in a single infinitely small instant. If this is meant to be an introductory post to teach calculus, it seems to be off on the wrong foot

  26. @CN: Whoops, thanks for the catch! Glad you liked it.

    @Integrating in Illinois (love the name): Good point — I clarified the statement above.

    Intuitively, I see infinitesimals separate from the “regular” small numbers we deal with (like 1E-30). That is, we can’t just multiply an infinitesimal by a large number (like 1E30) to bring it back to our scale.

    To make infinitesimals useful, we have to add an infinite amount of them (integrate), which is a new operation in our math vocabulary.

    So yes, infinitesimals can certainly be used to get real results (like areas of shapes, as you mention) but we need a new operation (integrals) to do it. I hope to make this more clear in future posts, thanks for the comment!

  29. First of all, I’m sorry for my (I suppose) bad english writing. I do better with spanish ;)

    It’s amazing how your explanations make me understand so well the math’s background. I believe that your method could be the best alternative to teach the math in every school grade, at least here, in México. It looks so interesting for almost anyone, ’cause it’s not just “telling how to solve hypothetical problems” thing… thats boring for almost every student. There is philosophy behind any theorem, theory or whatever requires a mathematical analysis.

    Thanks for all your posts.

  30. @Felix: Thanks for the wonderful note! Your English is still better than my Spanish, and I studied it for a while :) .

    I’m glad you’re able to enjoy the style of the site. Yes, I feel education has veered towards things that are easily testable/measurable (memorizing facts & plugging items into equations) instead of focusing on the deep insight which is more important, but can’t be measured. Thanks again for the comment!

  31. Brilliant. One of the best blogs I came across explaining fundamentals of math. Your thinking seems related to/influenced by (?) the Pythagoras “Science of numbers” and using numbers to understand the universe around us.

  32. @Mitra: Thanks for the kind words! I hadn’t heard of the “Science of numbers” but it sounds interesting. I have a curiosity about how things “really” work at an intuitive, not formulaic level. Thanks for dropping by.

  33. Great article with a lot of valid statements.

    However, the way you state your main thesis ultimately boils down to a confusion. You conflate numbers and numerals, ie. the symbols we use to represent numbers. This is an extremely fine distinction to make, and often a very difficult one, because often there is no consequence to confusing them, and humans are not good at abstraction.

    By way of example, consider “1”, which is the symbol we use to represent the unit number. This number is absolutely exact. It is exactly one number, and it is not identical with any other number. However, there is a second numeral for it! You can write the very same number as “0.999999…” with an infinitely continuing series of 9s. This is easy to show: both 0.999999…/3 and 1/3 are equal to 0.3333333…. So both “0.999999…” and “1” are the same number, even though the two representations look drastically different, and one of them goes on forever, so that it cannot be written down exactly.

    Likewise, “π” is the symbol we use to represent the ratio of the circumference of the unit square and the unit circle. This number is absolutely exact. It is exactly one number, and there is no other number that is identical with it. F.ex., you can say that a circle with radius 3 has exactly 3 times the circumference of a circle with radius 1. Both “3.141592…” and “π” represent the same, exact number… even though the two representations look drastically different and one of them goes on forever… so that it cannot be written down exactly. :)

    There is merely no way to represent π with a finite decimal numeral, but this does not mean that the number π is somehow any less exact than 1.

    Numbers are mathematical entities, so are absolutely exact. Numerals, in contrast, are human conventions invented in trying to use the finite, discrete materials of this universe (ink, luminescent dots on a screen, whatever) to represent numbers. (Calculus adds another distinction on top of that, but that is yet another issue.)

  34. @Aristotle: Thanks for the detailed comment! Yes, I agree with your clarification — there is a difference between the concept (the number or idea of 1) and our representation of it (the numerals). Speaking of which, I was planning on using the .9999… = 1 as an example of limits.

    The higher-level thought, that I may need to back and revise to make clear, is this: our numerals are finite, and thus have limited ability in describing certain numbers. That is, we cannot finitely describe pi using our numerals except to abstract it into a symbol, or give it as the result of a limiting process.

    Calculus helps us recognize that that our numerals are “limited”. Thanks again for the comment!

  36. I suppose the epsilon-delta example of limit is perhaps another good example besides the pixel example.

  37. Quick Question:

    Is this article saying that being precise is good but unneccesary?And isn’t pi 3.14596 ect?

  38. @Seamus: Great question. Precision is great, but infinite (perfect) precision is not necessary. Basically, the idea is to find what level of precision is “good enough” for your needs (and you can’t say you need perfect precision! :) ). For pi, 30 digits is far more than anyone needs for engineering purposes. Even 10 digits is extremely accurate — it’s far more likely that errors are being introduced by other measurements/tolerances, and not the imprecision in your expansion of pi.

  39. Brilliant. This site is a work of genius, it really is. Not just because you describe things well. Especially because you had the balls to put your intuitions about math online in a clear way that challenges most of our dearly held conventions. This article is not simply mathematics, it is philosophy. You correct many misconceptions students have about numbers and how they relate to life. Awesome work.

  40. i understand what you’re going for here, but don’t agree that proofs and concepts are separate

  41. i love this site!!! i can’t sleep right now cause i can’t stop reading your articles! i’m currently struggling with calculus. but i used to love math… before there was calculus. i wasn’t able to fully understand it before, since my professor did nothing to help me appreciate the subject. oh, and she failed more than half the class, including me. i freaked out, and i hated school. so, uhmm, thanks a lot!! now i’m beginning to appreciate the beauty of calculus. and once again, i love math! :) )

  42. @shelly: Awesome!!! I’m really glad it helped (and that you got addicted to the articles, heh), one of the best feelings is starting to overcome our inhibitions about a subject. Not everyone needs to be in love with math, but we can at least appreciate it as much as we do a good song or nice poem :) .

  44. the whole idea of “an infinitesimal” is so badly conceived as to be impossible to rehabilitate. so you have a positive number that, when added to some other number, leaves that number alone? OK, so what happens when we add “N” of them together, where “N” is an integer > 1/x (your “infinitesimal”)? yeah, suddenly the real numbers aren’t a field anymore, hey what’s the worst that can happen?

    there’s a reason the formal definitions of various limit statements were developed, and it has nothing to do with any kind of neurotic need for complication. moreover, my experience is that a ninth-grader in algebra two can master the implementation, despite the intimidating burden of notation.

    and the “infinity exists” is even worse- much worse. if you want to treat your own headaches by decapitation, that’s one thing, but let’s not advocate the procedure to impressionable young people, ok?

  45. Bump, just stumbled across this site and it looks great. Much respect for people who share their insights (whilst yearning for more) and help to educate others. Great work!

Leave a Reply

Your email address will not be published.

You may use these HTML tags and attributes: <a href="" title=""> <abbr title=""> <acronym title=""> <b> <blockquote cite=""> <cite> <code> <del datetime=""> <em> <i> <q cite=""> <strike> <strong>