A Friendly Chat About Whether 0.999… = 1

Does .999… = 1? The question invites the curiosity of students and the ire of pedants. A famous joke illustrates my point:

A man is lost at sea in a hot air balloon. He sees a lighthouse approaching in the fog. “Where am I?” he shouts desperately through the wind. “You’re in a balloon!” he hears as he drifts off into the distance.

The response is correct but unhelpful. When people ask about 0.999… they aren’t saying “Hey, could you find the limit of a convergent series under the axioms of the real number system?” (Really? Yes, Really!)

No, there’s a broader, more interesting subtext: What happens when one number gets infinitely close to another?

It’s a rare thing when people wonder about math: let’s use the opportunity! Instead of bluntly offering technical definitions to satisfy some need for rigor, let’s allow ourselves to explore the question.

Here’s my quick summary:

  • The meaning of 0.999… depends on our assumptions about how numbers behave.
  • A common assumption is that numbers cannot be “infinitely close” together — they’re either the same, or they’re not. With these rules, 0.999… = 1 since we don’t have a way to represent the difference.
  • If we allow the idea of “infinitely close numbers”, then yes, 0.999… can be less than 1.

Math can be about questioning assumptions, pushing boundaries, and wondering “What if?”. Let’s dive in.

Do Infinitely Small Numbers Exist?

The meaning of 0.999… is a tricky concept, and depends on what we allow a number to be. Here’s an example: Does “3 – 4″ mean anything to you?

Sure, it’s -1. Duh. But the question is only simple because you’ve embraced the advanced idea of negatives: you’re ok with numbers being less than nothing. In the 1700s, when negatives were brand new, the concept of “3-4″ was eyed with great suspicion, if allowed at all. (Geniuses of the time thought negatives “wrapped around” after you passed infinity).

Infinitely small numbers face a similar predicament today: they’re new, challenge some long-held assumptions, and are considered “non-standard”.

So, Do Infinitesimals Exist?

Well, do negative numbers exist? Negatives exist if you allow them and have consistent rules for their use.

Our current number system assumes the long-standing Archimedean property: if a number is smaller than every other number, it must be zero. More simply, infinitely small numbers don’t exist.

The idea should make sense: numbers should be zero or not-zero, right? Well, it’s “true” in the same way numbers must be there (positive) or not there (zero) — it’s true because we’ve implicitly excluded other possibilities.

But, it’s no matter — let’s see where the Archimedean property takes us.

The Traditional Approach: 0.999… = 1

If we assume infinitely small numbers don’t exist, we can show 0.999… = 1.

First off, we need to figure out what 0.999… means. Most mathematicians see the problem like this:

  • 0.999… represents a series of numbers: 0.9, 0.99, 0.999, 0.9999, and so on
  • The question: does this series get so close (converge) to a result that we cannot tell it apart?

This is the reasoning behind limits: Does our “thing to examine” get so darn close to another number that we can’t tell them apart, no matter how hard we try?

“Well,” you say, “How do you tell numbers apart?”. Great question. The simplest way to compare is to subtract:

  • if a – b = 0, they’re the same
  • if a – b is not zero, they’re different

The idea behind limits is to find some point at which “a – b” becomes zero (less than any number); that is, we can’t tell the “number to test” and our “result” as different.

The Error Tolerance

It’s still tough to compare items when they take such different forms (like an infinite series). The next clever idea behind limits: define an error tolerance:

  • You give me your tolerance for error / accuracy level (call it “e”)
  • I’ll see whether I can get the two things to fall within that tolerance
  • If so, they’re equal! If we can’t tell them apart, no matter how hard we try, they must be the same.

Suppose I sell you a raisin granola bar, claiming it’s 100 grams. You take it home, examine the non FDA-approved wrapper, and decide to see if I’m lying. You put the snack on your scale and it shows 100 grams. The scale is accurate to 1 gram. Did I trick you?

You couldn’t know: as far as you can tell, within your accuracy, the granola bar is indeed 100 grams. Our current problem is similar: I’m selling you a “granola bar” weighing 1 gram, but sneaky me, I’m actually giving you one weighing 0.999… grams. Can you tell the difference?

Ok, let’s work this out. Suppose your error tolerance is 0.1 gram. Then if you ask for 1, and I give you 0.99, the difference is 0.01 (one hundredth) and you don’t know you’ve been tricked! 1 and .99 look the same to you.

But that’s child’s-play. Let’s say your scale is accurate to 1e-9 (.000000001, a billionth of a gram). Well then, I’ll sell you a candy bar that is .999999999999 (only one trillionth of a gram off) and you’ll be fooled again! Hah!

In fact, instead of picking a specific tolerance like 0.01, let’s use a general one (e):

  • Error tolerance: e
  • Difference: Well, suppose e has “n” digits of precision. Let 0.999… expand until we have a difference requiring n+1 digits of precision to detect.
  • Therefore, the tolerance can always be less than e! And the difference appears to be zero.

See the trick? Here’s a visual way to represent it:

visualizing 0.999...

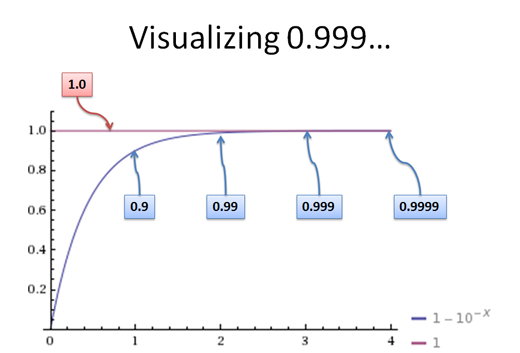
The straight line is what you’re expecting: 1.0, that perfect granola bar. The curve is the number of digits we expand 0.999… to. The idea is to expand 0.999… until it falls within “e”, your tolerance:

beating the error margin

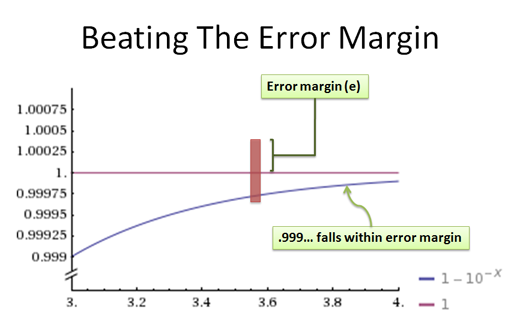
At some point, no matter what you pick for e, 0.999… will get close enough to satisfy us mathematically.

(As an aside, 0.999… isn’t a growing process, it’s a final result on its own. The curve represents the idea that we can approximate 0.999… with better and better accuracy — this is fodder for another post).

With limits, if the difference between two things is smaller than any margin we can dream of, they must be the same.

Assuming Infinitesimals Exist

This first conclusion may not sit well with you — you might feel tricked. And that’s ok! We seem to be ignoring something important when we say that 0.999… equals 1 because we, with our finite precision, cannot tell the difference.

Newer number systems have developed the idea that infinitesimals exist. Specifically:

  • Infinitely small numbers can exist: they aren’t zero, but look like zero to us.

This seems to be a confusing idea, but I see it like this: atoms don’t exist to cavemen. Once they’ve cut a rock into grains of sand, they can go no further: that’s the smallest unit they can imagine. Things are either grains, or not there. They can’t imagine the concept of atoms too small for the naked eye.

Compared to other number systems, we’re cavemen. What we call “tiny numbers” are actually gigantic. In fact, there can be another “dimension” of numbers too small for us to detect — numbers that differ only in this tiny dimension look identical to us, but are different under an infinitely powerful microscope.

I interpret 0.999… like this: Can we make a number a bit less than 1 in this new, infinitely small dimension?

Hyperreal Numbers

Hyperreal numbers are one system that uses this “tiny dimension” to examine infinitely small numbers. In this, infinitesimals are usually called “h”, and are considered to be 1/H (where big H is infinity).

So, the idea is this:

  • 0.999… < 1 [We're assuming it's allowed to be smaller, and infinitely small numbers exist]
  • 0.999… + h = 1 [h is the infinitely small number that makes up the gap]
  • 0.999… = 1 – h [Equivalently, we can subtract an infinitely small amount from 1]

So, 0.999… is just a tiny bit less than 1, and the difference is h!

Back to Our Numbers

The problem is, “h” doesn’t exist back in our macroscopic world. Or rather, h looks the same as zero to us — we can’t tell that it’s a tiny atom, not the lack of any matter altogether. Here’s one way to visualize it:

infinitesimal difference

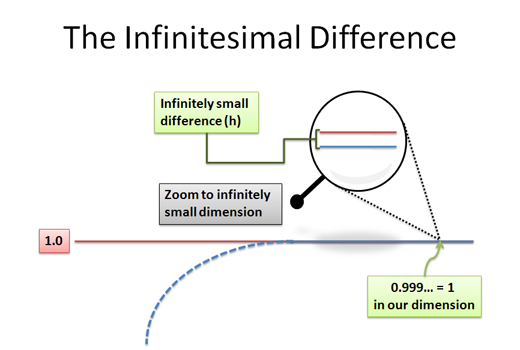
When we switch back to our world, it’s called taking the “standard part” of a number. It essentially means we throw away all the h’s, and convert them to zeroes. So,

  • 0.999… = 1 – h [there is an infinitely small difference]
  • St(0.999…) = St(1 – h) = St(1) – St(h) = 1 – 0 = 1 [And to us, 0.999... = 1]

The happy compromise is this: in a more accurate dimension, 0.999… and 1 are different. But, when we, with our finite accuracy, try to describe the difference, we cannot: 0.999… and 1 look identical.

Lessons Learned

Let’s hop back to our world. The purpose of “Does 0.999… equal 1?” is not to spit back the answer to a limit question. That’s interpreting the query as “Hey, within our system what does 0.999… represent?”

The question is about exploration. It’s really, “Hey, I’m wondering about numbers infinitely close together (.999… and 1). How do we handle them?”

Here’s my response:

  • Our idea of a number has evolved over thousands of years to include new concepts (integers, decimals, rationals, reals, negatives, imaginary numbers…).
  • In our current system, we haven’t allowed infinitely small numbers. As a result, 0.999… = 1 because we don’t allow there to be a gap between them (so they must be the same).
  • In other number systems (like the hyperreal numbers), 0.999… is less than 1. Here, infinitely small numbers are allowed to exist, and this tiny difference (h) is what separates 0.999… from 1.

There are life lessons here: can we extend our mental model of the world? Negatives gave us the conception that every number can have an opposite. And you know what? It turns out matter can have an opposite too (Dark matter destroys regular mass when they come in contact, just like 3 + (-3) = 0).

Let’s think about infinitesimals, a tiny dimension beyond our accuracy:

  • Some theories of physics reference tiny “curled up” dimensions which are embedded into our own. These dimensions may be infinitely small compared to our own — we never notice them. To me, “infinitely small dimensions” are a way to describe something which is there, but undetectable to us.
  • The physical sciences use “significant figures” and error margins to specify the inherent inaccuracy of our calculations. We know that reality is different from what we actually measure: infinitesimals help make this distinction explicit.
  • Making models: An infinitely small dimension can help us create simple but accurate models to solve problems in our world. The idea of “simple but accurate enough” is at the heart of calculus.

Math isn’t just about solving equations. Expanding our perspective with strange new ideas helps disparate subjects click. Don’t be afraid wonder “What if?”.

Appendix: Where’s the Rigor?

When writing, I like to envision a super-pedant, concerned more with satisfying (and demonstrating) his rigor than educating the reader. This mythical(?) nemesis inspires me to focus on intuition. I really should give Mr. Rigor a name.

But, rigor has a use: it helps ink the pencil-lines we’ve sketched out. I’m not a mathematician, but others have written about the details of interpreting 0.999… and 1 or less than 1:

“So long as the number system has not been specified, the students’ hunch that .999… can fall infinitesimally short of 1, can be justified in a mathematically rigorous fashion.”

My goal is to educate, entertain, and spread interest in math. Can you think of a more salient way to get non-math majors interested in the ideas behind analysis? Limits aren’t going to market themselves.


Posted November 19, 2009, under Calculus, Math
Tags:
Related Posts:
  • Math Webinar Sat 6/19/2010 @ 2pm EST
  • A Simple Introduction To Computer Networking
  • How To Make a Bookmarklet For Your Web Application
  • What You Should Know About The Stock Market

    • BetterExplained: Get the eBook

    Like the site? Take it with you. Develop your math sense using insights, not memorization.

    66 Comments »

    Trackbacks & Pingbacks

    1. Trackback by MathFail.com — December 1, 2009 @ 3:48 pm

    2. Pingback by Intuition Failure « Ishango Bones — February 25, 2010 @ 4:58 pm

    3. Pingback by Is 0.999… really equals 1? « Mathematics and Multimedia — June 3, 2010 @ 3:02 pm


    Comments

    1. My Calculus prof proved this for us in class.

      Let N = 0.999…

      Assume N = 1, now multiply both sides by 10
      10N = 10, now subtract 9 from both sides
      N = 1

      I *think* that’s how he did it.

      Aaron — December 1, 2009 @ 5:49 am

    2. Why “0.999 = 1″ is counter-intuitive:

      If you have “0.99″ instead of “0.9″, it means that you are one step closer to 1, as close as the 10-digit-notation allows in one step, *but without reaching 1*. If you add another 9 and arrive at “0.999″, you have again stepped as close to 1 as you could in one step, but without reaching 1.

      Even if you would do this an infinite amount of times, *every step* would have the same rule: “… *without* reaching 1″.

      some bla guy — December 1, 2009 @ 6:31 am

    3. Last year I wrote about it (albeit in Italian) at
      http://xmau.com/mate/art/0-999999a.html and http://xmau.com/mate/art/0-999999b.html . My line of reasoning is more or less like yours :-) (oh yeah, there’s also http://xmau.com/mate/art/0-999999c.html where I wonder about the difference between 1.00 and 1, and ramble about the measuration errors!)

      .mau. — December 1, 2009 @ 6:51 am

    4. Ever head of this guy Cauchy? He might wanna have a word with you.

      some bla guy — December 1, 2009 @ 6:51 am

    5. i really like your explanations of tricky math concepts. do keep posting more good stuff like this. looking forward to your post on approximating functions :)

      also from what i understand, dark matter is different from anti-matter. When matter meets anti-matter they annihilate and release energy. Anti-matter is well understood while dark matter is not. It is simply conjectured to exist to explain the speeding up of the expansion of the universe when it should really be slowing down. So you can make that (infinitesimal) correction into your excellent post :)

      ram — December 1, 2009 @ 7:29 am

    6. I think you meant anti-matter where you said “Dark matter destroys regular mass when they come in contact [...])

      Darkie — December 1, 2009 @ 7:32 am

    7. The hyperreal case is a little bit more subtle than that.

      See, the object 0.999…, as you understand it, doesn’t quite exist there. The hyperreals add infinitesimals to the real line by also adding infinitely large numbers, including infinitely large integers. And since {0, 0.9, 0.99, 0.999, …} is a sequence on the positive integers, it gets a lot more terms when it gets embedded into the hyperreal system; it becomes a hyper-sequence, for lack of a better term. Canonically it corresponds to a hyper-sequence whose length is unbounded even in the hyperreals, and still has 1 as a limit.

      Now, we could also look at the hyper-sequence which started the same way, but stopped getting bigger at some hyper-integer w. The difference between 1 and that limit would be 10-w, which is positive in our system. (This is what the arXiv paper you cited is talking about.) There are many sequences which are increasing like 0.999… on the standard integers, then take a constant value x on most of the nonstandard integers, but x could be anything.

      So the real problem is that 0.999… isn’t well-defined in the hyperreals—it doesn’t really equal anything. I know of no context where 0.999… has a clear resolution and it isn’t 1.

      (And for the record, we aren’t rigorous because we like to be. We’re rigorous because the subject demands rigor. Intuition fails a lot.)

      Chad Groft — December 1, 2009 @ 8:02 am

    8. sorry, 10-w should be 10^(-w)

      Chad Groft — December 1, 2009 @ 8:04 am

    9. some bla guy — I think you’re right about why 0.999… = 1 is a counter-intuitive fact, but there’s an easy counter. Each finite term 0.99…9 is larger than the previous term; so the “infinite term” 0.999… is larger than all the finite terms. So the fact that 1 is larger than 0.99…9 isn’t an obstacle; in fact, it’s a requirement.

      Chad Groft — December 1, 2009 @ 8:12 am

    10. Oh, since I’m here anyway:

      Aaron — Any proof that assumes N = 1 to prove N = 1 is dead in the water. The usual “proof” goes like this: If (1) N = 0.999…, then (2) 10N = 9.999…; subtract (1) from (2) to get (3) 9N = 9, from which N = 1. I say “proof” because first you have to establish that arithmetic with infinite expansions makes sense, and it’s usually easier to do some other proof instead.

      ram — Your broad point is correct, but what you’ve described is “dark energy”. Dark matter is mass that we know must exist, because of its gravitational effect on visible objects near it, but can’t see, because it doesn’t interact with the electromagnetic field. I’m pretty sure it would actually slow the expansion of the universe, but don’t quote me on that.

      Chad Groft — December 1, 2009 @ 8:37 am

    11. I always use this quick explanation to the layman:
      1/3 (one third) can be represented by 0.333…
      If you take each thirds and add them up (0.333.. + 0.333… + 0.333…) they add up to 1.0, not 0.999…

      haileris — December 1, 2009 @ 10:36 am

    12. A very simple way to solve this:

      Take two numbers 3 and 5; now, to see if they are equal we can try to find a number between them. Well, a number like 4 or 3.75 is between.

      So, now let’s take 0.999… and 1.0. Can you find a number that is between an infinitely repeating set of 9’s before it goes to 1? No, there is no number between 0.999… and 1. If you truly figure 0.999… as an infinite string of 9’s then there is nothing before you would have to round up to 1.

      However, for practical purposes we have to round to a finite number. A finite string of 0.9999’s is only equal to one because humans can’t work/comprehend an infinite string of 9’s.

      Adam — December 1, 2009 @ 4:28 pm

    13. You object that, when asked whether .99999…=1, we view .99999… within “our system”, whatever that means. Well, of course we do! How else could we possibly interpret the question or try to answer it?

      When someone asks whether .999… equals 1, they are most certainly asking within the context of the real numbers. Switching gears and trying to interpret the question within the hyperreals is as arbitrary and evasive as choosing to instead view it in the p-adics, where another different (but equally valid) answer could be given.

      This is silly. This “argument” really needs to be put to rest. Mathematical rigor exists precisely for this reason.

      Jeff - a mathematician — December 1, 2009 @ 5:51 pm

    14. Ah, I knew this would this would invite the curiosity of students and the ire of pedants! :)

      @Aaron: Great question. These types of proofs make assumptions about how addition and subtraction would work with these infinite decimals (does 9 * 0.999 = 8.999…?), but they do work for the regular number system (see http://math.fau.edu/Richman/HTML/999.htm).

      @some bla guy: I’d love to have a word with Cauchy — I bet he’d be interested in learning about new number systems that can rigorously approach the same problems differently!

      @mau: Neat — I’ll have to see how well Google translate does at math :) .

      @ram: Whoops, thanks for the correction! Yes, I meant anti-matter :) .

      @Chad: Great points, thanks for the discussion! I guess it depends on the meaning of 0.999…, which is indeed ambiguous. I think the better phrasing may be “The hyperreal number uH=0.999…;…999000… with H-infinitely many 9s, for some infinite hyperinteger H, satisfies a strict inequality uH < 1" (from Wikipedia).

      I think the higher meta-point is figuring out the question behind the question — the layman isn’t asking about 0.999… as constructed in the real number system. They want to know what happens when one number gets “infinitely close” to another — can this be represented? 0.999… is the most convenient form of this question (also see 1/infinity — does this equal 0? Yes, if you take the limit approach, no if you take the hyperreal).

      @haileris: Does 1/3 = .333.. exactly, or is 0.333… different at the infinitely small level? :)

      @Adam: Great point — because our current number system cannot represent the difference between 0.999… and 1 (there’s no number in-between), in our current system they are equal. However, other systems allow it, so I take the approach of “it depends”.

      @Jeff: Thanks for dropping in, but I disagree that it needs to be put to rest. Transform the problem: if it’s 1600 and someone asks 1600s Jeff what does sqrt(-1) mean, what do you say? That they are asking this question in the context of the real numbers, and the answer is undefined? How else do you answer it?

      The alternative is to explore a new number system (complex numbers, hyperreal numbers) and see if it has interesting properties. You can’t take the question at face value, it’s really about exploring the nature of infinitely small numbers.

      Kalid — December 1, 2009 @ 6:32 pm

    15. Hailis has the answer and yes, Kalid, 1/3 _does_ equal 0.333… The numerator is really 1.000… and the division continues ad infinitum. To say that 0.999… does not equal 1 is to say that neither 3/3 nor 9/9 equal 1. I would love to hear your explanation as to why the rules for reducing 9/9 are different than those for reducing 8/8 or, for that matter, 1/1.

      Additionally, I don’t think there is much assumption involved when considering how addition might work with these particular infinitely repeating decimals. Try adding 1/3 and 1/7. When expressed as a decimal, each has an infinitely repeating sequence; yet we can identify a very specific and uncontroversial answer: 10/21.

      If we were discussing 0.12341234… it might be a different story; that number is not rational. 0.989898… comes close to 1 but never touches, which makes it an interesting candidate for the tolerance and accuracy portions of this discussion. But nobody is proposing that 0.989898… equals 1.

      0.9… is indeed a special case, but it is not the number-line equivalent to infinitely-close-but-not-touching (like the way my fingers don’t actually touch my keyboard as I type – there is a tiny gap between the atoms). 0.9… is 9 * 1/9. It’s a concept we can imagine and denote, but it doesn’t really exist as a unique number. It is, in truth, 1.

      Ogre_Kev — December 1, 2009 @ 9:58 pm

    16. About the “ire of pedants” … There is no point discussing infinity unless you are being pedantic and rigorous.

      Igor Ostrovsky — December 1, 2009 @ 10:25 pm

    17. Since we’re wondering out loud, I will say that this kind of number theory issue makes me wonder whether complex number are more real than real numbers.

      Michael F. Martin — December 2, 2009 @ 10:47 am

    18. @Ogre_Kev: I agree that in the current real number system, .333… = 1/3. But what this means is this:

      “The infinite sequence (.3, .33, .333, .3333…) converges to the limit 1/3″, which is another way of saying “We can make an element of (.3, .33, .333…) as close to 1/3 as we wish”.

      You might want to check out http://math.fau.edu/Richman/HTML/999.htm:

      “Perhaps the situation is that some real numbers can only be approximated, like the square root of 2, whereas others, like 1, can be written exactly, but can also be approximated. So 0.999… is a series that approximates the exact number 1. Of course this dichotomy depends on what we allow for approximations. For some purposes we might allow any rational number, but for our present discussion the terminating decimals—the decimal fractions—are the natural candidates. These can only approximate 1/3, for example, so we don’t have an exact expression for 1/3″.

      So, as long as we stay in the real number system, 1/3 is the limit of .333… [which is fine, but we don't have to stay in the real number system; others can capture the idea of what we mean when we say infinitely close].

      As a side comment: if 3/10 is not 1/3, and 33/100 is not 1/3, at what point does another digit make it exactly 1/3? This is a bit like Zeno’s paradoxes, which have not been fully resolved :) . The meta-point is that we can make that sequence as close to 1/3 as we need, which in the real number system means they are equal in the limit.

      @Igor: I think it’s possible to sketch out ideas intuitively and return with rigor to cement the foundation — Calculus developed this way, did it not?

      @Michael: Great question — I think all numbers may be equal abstractions of the mind. The real number system may be “less real” because it’s more limited than others.

      Kalid — December 2, 2009 @ 11:46 am

    19. “The infinite sequence (.3, .33, .333, .3333…) converges to the limit 1/3″, which is another way of saying “We can make an element of (.3, .33, .333…) as close to 1/3 as we wish”.

      Not exactly. It means that most of the elements of {.3, .33, .333, …} are close to 1/3. Here “most” means “all but finitely many”, and “close” means “within any predetermined positive distance”. That’s how you get that limits are uniquely determined. The terms of a sequence can’t all be clustered around a and all be clustered around b.

      “As a side comment: if 3/10 is not 1/3, and 33/100 is not 1/3, at what point does another digit make it exactly 1/3?”

      There isn’t one. The limit of the sequence is not (generally) a term of the sequence. See comment #9 (my response to “some bla guy”).

      “This is a bit like Zeno’s paradoxes, which have not been fully resolved.”

      Sure they have, in large part by the limit concept. (If they hadn’t been resolved, even Newtonian physics wouldn’t be possible.)

      “The meta-point is that we can make that sequence as close to 1/3 as we need, which in the real number system means they are equal in the limit.”

      Limits are unique in the hyperreals as well. You might have infinitesimal separations, but you also have infinitesimal resolving power (if that makes sense). Be careful here: a lot of “standard” sequences with limits, such as {.3, .33, .333, …}, don’t have limits in the hyperreals unless you make some canonical extension to a hypersequence; if you do that, the extension will still have the original limit (in this case 1/3).

      “The real number system may be “less real” because it’s more limited than others.”

      Not so much. See, the construction that Robinson applied to the reals to get the hyperreals can also be applied to the hyperreals. If we call the result the hyperhyperreals, well, we can apply the construction again, to get the (hyper)^3-reals, and so forth. Each is “less limited” than the previous, but none of these can be the “real” system, because each is “more limited” than the next. But really, none of these is more limited than the others, because the same expressible facts are true in all of them.

      To me, the “real” system is the simplest system which easily models the phenomena we’re interested in—which in this case is the ordinary real line.

      Chad Groft — December 2, 2009 @ 7:36 pm

    20. By the way, you might read Fred Richman’s article a bit more carefully. The system he creates is one in which 0.99… and 1 resolve differently, but it’s also one in which negation and multiplication don’t make sense. So, fair enough, such systems exist, but I wouldn’t want to work in any of them.

      Chad Groft — December 2, 2009 @ 7:41 pm

    21. @Chad: Thanks for the info & discussion! I’m not rigorously versed in the details, so am learning as I go along :) . As far as how “Does 0.999… = 1?” is interpreted by most mathematicians, here’s my guess:

      * 0.999… means “continue .999 in the obvious way”
      * It is not common to define real numbers as a sequence of decimal digits (though not impossible). We prefer to construct a real number as a Cauchy Sequence of rationals (for example).
      * 0.9, 0.99, 0.999, … is the obvious Cauchy Sequence representing that infinite decimal expansion
      * Now that we have a sequence, I see you are using the equals operator. Like a compiler doing integer to floating point conversion, I’m going to “cast” the sequence into a real number (if possible) by taking the limit of the sequence, and compare that to 1.

      So, as long as we’re staying within the real number system, 0.999… interpreted this way means 1 (and .333… = 1/3). But is that the only interpretation? If we interpret 0.999… as possibly referring to a hyperreal number (1 – h) then what conclusions can we draw?

      I think there’s a notion of an “infinitely small gap” that’s we cannot describe with real numbers that leads to interesting approaches.

      It’s interesting to me that early physics was developed with the use of “non-rigorous” infinitesimals; clearly there is a concept there (being able to manipulate dy and dx independently, not taking them as an operator) that was not captured in the current real number system. If there’s a number system (the hyperreals) which can explicitly capture that idea (vs. breaking the rules in the current one) I think it’s more useful for that purpose.

      So, by “limited” I don’t mean less capable, but not as innately useful/expressive (you probably know, but most programming languages are equally powerful (Turing Complete) but differ vastly in how useful/usable they are). I agree about the hyper^N reals, I had suspected that too :) . But I don’t know of situations where we’re trying to solve problems by relying on 2nd-order infinitesimals and having to work around it in the current one — if we were, I’d suggest that system as the most expressive.

      I appreciate the clarification on the Richman piece — he does say it’s an open problem. I’m interested in going through http://www.jstor.org/pss/2316619 which expounds on infinitesimals and their representations further (http://en.wikipedia.org/wiki/0.999…#Infinitesimals).

      Kalid — December 2, 2009 @ 9:35 pm

    22. No problem—this whole discussion is helping me clarify a lot of these ideas as well.

      Here’s the thing: if you want to do calculus with infinitesimals, first you have to do arithmetic with them. And that leads to problems, if you also try to do arithmetic with infinite decimal expansions. If you want .99… to resolve to 1 – h, with h infinitesimal but nonzero, then does 1.99… resolve to 2 – h or 2 – 2h? Both make sense. (And don’t say that 2 x .99… is 1.99…8. That has an 8 in the “last place”, and there is no last place.)

      Interestingly, though, if we let go of decimal expansions and consider arbitrary sequences of numbers, we get awfully close to hyperreals. In one “hyper” construction, the hyperreals are precisely the sequences of reals modulo a certain equivalence relation. Sequences which have equal terms at most indices are considered equal, and statements which are true at most indices are considered true.

      For example, {1,2,3,…} represents an infinitely large number (on account of most natural numbers are larger than x for any fixed real number x); call this number w. Its reciprocal sequence {1,1/2,1/3,…} represents the infinitesimal 1/w, and {.1, .01, .001, …} represents the infinitesimal 10^(-w) (which we’ll call h), and {.9, .99, …} represents 1 – h; but {0, .9, .99, …} represents 1 – 10h, so there’s some nasty ambiguity in (.99…). Also {1.9, 1.99, 1.999, …} represents 2 – h, and {1.8, 1.98, 1.998, …} represents 2 – 2h. So we can get enough infinitesimals to do calculus, but we have to go beyond decimal expansions to do it.

      “We prefer to construct a real number as a Cauchy Sequence of rationals (for example).”

      Since we’re being technical here anyway: Cauchy sequences of rationals only represent real numbers. We still have to specify when two Cauchy sequences represent the same real number; and {a_n} and {b_n} do this precisely when {a_n – b_n} converges to 0 in the rationals. In particular, {1, 1, 1, …} and {.9, .99, .999, …} represent the same real number (which is 1), because {.1, .01, .001, …} converges to 0.

      I’ll stand by my original position, more or less: there’s no unambiguous way to interpret the infinite decimal expansion of a fraction x as “infinitesimally less” than x, and still be able to do arithmetic with those decimal expansions. The Wikipedia article you cite backs me up on this, at the end of its introduction: “[S]ome settings contain numbers that are ‘just shy’ of 1[, but] these are generally unrelated to 0.999…”.

      “So, by “limited” I don’t mean less capable, but not as innately useful/expressive (you probably know, but most programming languages are equally powerful (Turing Complete) but differ vastly in how useful/usable they are)”.

      That’s exactly what I’m talking about. The statements which are true on the real numbers are exactly those which are true on the hyperreals — if you’re careful about how you interpret those statements. Nonstandard analysis—that is, analysis with the hyperreals—hasn’t really caught on, and I suspect it’s because proper interpretation is just as difficult to deal with as epsilon-delta argument, with no real gain.

      It might be useful to write a nonrigorous calculus textbook based on nonstandard analysis; in fact, I think it’s been done.

      Chad Groft — December 3, 2009 @ 5:11 pm

    23. (Geniuses of the time thought negatives “wrapped around” after you passed infinity)

      I am not sure if this is a statement of derision or fact. The idea that the negatives “wrap around” is not that far fetched. The 1 point compactification of the reals is homeomorphic with the circle. In that context it makes perfect sense to think of the negatives as wrapping around at infinity. I allow my students to use the analogy frequently with asymptotes.

      Jason Stein — December 16, 2009 @ 5:46 am

    24. I have a few questions. They may sound like objections, but they’re definitely in question form because I am admittedly slightly out of my depth here. These are the main trip-ups that are keeping me from wrapping my mind around what you’re saying:

      How does the fact that we’re working all this stuff about 0.999… in base 10 effect the issue? If it’s not equal to 1, then it’s obviously not a rational number, but can it be expressed, or even approximated, in other bases? In this alternate number system you propose, is 0.777… in base 8 equal to 0.999… in base 10?

      And I know this has been touched on in the comments already, but I’m still wondering about the (1/3)*3=1 angle. I take it that in this new system, (1/3) wouldn’t be equal to 0.333…, for the same reasons as with 0.999… and 1. So does this mean that (1/3) cannot be calculated?

      Stephen — December 22, 2009 @ 3:20 am

    25. Stephen: To an extent, base doesn’t matter. If we take 0.9… in base 10 as infinitesimally less than 1, then the same is true of 0.1… in base 2, and 0.7… in base 8, and so forth. And you’re right about 0.3…; under this scheme, it would be infinitesimally less than 1/3. The problems show up when you try to nail down that infinitesimal and do arithmetic. Consider the argument I make in #22: if 0.9… = 1 – h, do we have 1.9… = 1 + 0.9… = 2 – h, or do we have 1.9… = 2*(0.9…) = 2 – 2h?

      Come to think of it, this is a better argument for 0.9… = 1 than the 3*(1/3 = 0.3…) idea, because it eliminates the possibility of “infinitesimal separation” entirely. These last two equations are consistent precisely when h = 0.

      I’m not quite sure what you mean by “1/3 cannot be calculated”. It would mean than no decimal expansion evaluates to precisely 1/3. However, since “infinitesimal separation” falls apart when we try to be precise and do arithmetic with it, this is an academic concern.

      Chad Groft — December 22, 2009 @ 7:26 am

    26. Incidentally, there *is* an elementary calculus text which uses the hyperreals, written by H. Jerome Keisler and freely available.

      Chad Groft — December 22, 2009 @ 7:28 am

    27. @Chad: Thanks for the discussion and for helping out with the questions! Yes, Keisler’s book seems to be an excellent resource, and I’m going through it to really understand calculus at a deeper level than when I studied it originally (many proofs seem to fall into place using “algebra”, like the proof of the product rule).

      All of this has got me thinking about analysis — I’m sure I’ve made some technical errors in the post that I need to correct. The goal is to start the discussion and embrace the idea of infinitesimals :) .

      @Jason: Not meant to be a statement of derision, but more “The geniuses can have trouble thinking about new when they are first introduced, too”. That’s really interesting that the negatives can take that interpretation — though I’d be very surprised and impressed if that’s what Euler and others had in mind. The meta point being that we present math all neatly packaged up, even though it took centuries of debate and revision to get there [like pretending Shakespeare wrote his plays in a single draft, a single sitting, and implying to students "that's how poetry is done"].

      Actually, I wonder if this has come full circle: negatives were thought to wrap around, this interpretation was ignored/found not useful by many (the majority of people do not know this interpretation, I posit), but later found useful. Infinitesimals were first thought to be useful (Leibniz), later thought nonrigorous by the majority, and then later found to be useful and rigorous.

      Kalid — December 31, 2009 @ 5:16 pm

    28. It’s simply hard to envision hyperreal numbers doing to mathematics what complex numbers did. Chad’s examination solidifies my view.

      On the other hand, I have read much of the Jerome Keisler book. I think that someone who truly understands Calculus through the conventional approach is on equal footing with one who understands it through the infinitesimal approach. However, understanding comes more easily, at least for me, from the latter. The major benefit is that “infinitesimal calculus” comes with the visual interpretation.

      Nobody — January 2, 2010 @ 7:07 am

    29. I love that the article is titled “a _friendly_ chat…” and starts with lambasting the supposed ire of pedants.

      Who finds infinitesimals useful now – how were they used recently?

      cyrano — January 7, 2010 @ 4:36 pm

    30. x = 0.999…
      10x = 9.99…
      10x-x = 9.99… – 0.999…
      9x = 9
      x = 1

      Nicole S. — January 28, 2010 @ 8:26 pm

    31. I was going to post that same proof!

      I don’t get the “if you use a new system, 0.999… does not equal 1″ bit. If they weren’t equal then there would be a fault with that simple proof.

      Rick — February 1, 2010 @ 12:16 pm

    32. #31: There’s no “fault” with the proof, but consider all the hidden premises. In order for #30 to work, we must have a unique interpretation of integer numerals and infinite decimals as numbers, and notions of +, -, *, / that do what we expect. If anything there fails in a given number system, the proof tells us nothing about that system.

      Give you an example: Let Q be the set of rational numbers, and let Q* be the set of all downward closed subsets of Q. That is, if X is an element of Q*, then it is a subset of Q, and if p ∈ X and q < p is rational, then q ∈ X. Q* then is ordered by the subset relation ⊂.

      What sets exactly does Q* contain? Well, the empty set qualifies: everything it contains is a rational number (because it doesn't contain anything), and it's downward closed for similarly silly reasons. Also the entire set Q qualifies: it's a subset of itself, and downward closed (because it contains all rationals, less than p or not). Beyond that, take any real number x; then the sets xlow = { p ∈ Q : p < x } and xhigh = { p ∈ Q : p ≤ x } are in Q*. xlow and xhigh are distinct precisely when x is rational. It can be shown that every element of Q* takes this form, and that they’re all distinct.

      Now: let’s say we interpret every integer or rational numeral n as the set nhigh. And let’s say we interpret the infinite decimal 0.abcdefg… as the set of all rationals p where p ≤ 0.a or p ≤ 0.ab or p ≤ 0.abc or … (which would be well-defined). Then the interpretation of 0.999… would be precisely 1low, which is distinct from 1high, which is our interpretation for 1. Similarly 0.333… would evaluate to (1/3)low.

      This whole interpretation is at least superficially reasonable. And #30 doesn’t apply, because we haven’t even defined +, -, *, /, let alone verified that they behave sanely.

      If we tried to do that, we’d quickly have to eliminate ∅ and Q as valid numbers, and identify plow with phigh, at which point we’d essentially have Dedekind’s construction of the real line. But if we don’t bother with arithmetic, we can interpret rationals and infinite decimals reasonably and still not have 0.9… = 1.

      Chad Groft — February 1, 2010 @ 1:59 pm

    33. Apparently this blog doesn’t recognize the <sub> tag. I hope what I write is still comprehensible.

      Chad Groft — February 1, 2010 @ 2:02 pm

    34. @Chad: Thanks for the details! I totally agree about the hidden premises.

      Intuitively, I also see the argument like this:
      “Can x^2 = -1? Well, if x is positive, x * x = positive. But if x is negative, x * x = positive. And if x = 0, x * x = 0. Therefore, sqrt(-1) cannot exist”.

      There’s a hidden premise about what x is allowed to be.

      So, looking at the argument

      x = 0.999…
      10x = 9.999…
      10x – x = 9.999… – 0.999…
      9x = 9.0

      We need to take a break and see what’s happening. Does 9x = 9.0? Hrm. Let’s multiply it out
      9(.9) = 8.1
      9(.99) = 8.91
      9(.999) = 8.991
      9(.9999) = 8.9991

      And so on. So is 9 really the same as 8.999…1? :) .

      In fact, if we look at the limits involved, it’s a restatement of the first equality. Let’s assume each limit has an implicit n->inf.

      x = lim[ 1 - 1/10^n]
      10x = 10 lim[1 - 1/10^n]
      10x – x = 10 lim[1 - 1/10^n] – lim[1 - 1/10^n]
      9x = lim[(10 - 1) - 10/10^n + 1/10^n]
      9x = lim[9 - 9/10^n] => this is where we get 8.1, 8.91, 8.991…
      x = lim[1 - 1/10^n]

      It seems the argument is a bit of a tautology, and reduces again to x = lim[1 - 1/10^n]. The question is then whether this is exactly 1. It is, if we disallow the idea of a number too small to detect with the reals (like disallowing an imaginary number). But if we allow the possibility of a difference in our premises, then we can state that x = 1 – h [where h is that tiny infinitesimal difference we couldn't notice with the reals].

      I’m not sure how rigorous this is (it probably isn’t) but it’s how I’m starting to see the implicit assumptions in the 10x – x argument.

      Kalid — February 5, 2010 @ 2:47 am

    35. I usually would explain this by saying, lets find out the difference between 1 and 0.999…

      Subtraction!

      1.000… -
      0.999…
      ——–
      0.000…

      If you follow the subtraction to infinity and beyond your answer of the difference is 0.000…

      So if the difference between 0.999… and 1 is 0.000… that means there is no difference between the two!

      0.999… is an artefact of the decimal system, because some values cannot be represented by terminated decimals. e.g. 1/3 or 0.333…

      If you argue about whether 0.999… is or isn’t equal to 1, then you need to argue if 0.333… is or isn’t equal to 1/3. Along with a whole bunch of other numbers which don’t have terminating representations in decimal.

      The problem comes from infinity being involved. Damn you infinity! And people’s ideas that a number is an exact thing, how can there be more than one way of representing 1?

      But we have n^0, n/n, cos(0).

      Andrew — February 5, 2010 @ 7:02 am

    36. Oh so one last thing.

      Is 0.000… equal to 0?

      :P

      Andrew — February 5, 2010 @ 7:05 am

    37. Dark matter vs Anti-matter

      You say that (Dark matter destroys regular mass when they come in contact, just like 3 + (-3) = 0).

      Assuming you mean Anti-Matter this also isn’t correct.

      Matter is not destroyed, it is converted to energy.

      The equation is more like

      3 matter + 3 anti-matter = 6 energy.

      I don’t think anyone has managed to find a case for when the law of conservation of energy is not true.

      Andrew — February 5, 2010 @ 7:57 am

    38. Andrew: That’s what I was arguing at first. Here’s the problem: how do you know that subtraction from the left, as you’re doing, is valid? It’s one thing to explain an idea, and quite another to defend the same idea against a skeptic. You have to go back to common ideas, possibly to first principles, and then you have to defend those principles intuitively.

      Kalid: No, 9 ≠ 8.99…91, because there’s no such number as 8.99…91. Not with infinitely many 9’s hidden in the “…”, anyhow. However, we do have 8 < 8.1 < 8.9 < 8.91 < 8.99 < … so the two “intertwined” sequences should have a common limit (if they have one at all), and your argument can be taken to show that 9*(0.9…) = 8.9….

      For the real numbers, the intuition is that of “continuous quantity”, or “length”. We can add and subtract lengths; we can agree on a unit length and use it to multiply and divide (otherwise length*length = are and length/length = ?); and we can compare lengths. Moreover all these operations are compatible in ways that are familiar to anyone who made it through high school math (commutative, associative, distributive, etc.).

      But that’s not quite enough to get all the possible lengths. There should be a quantity x where x^2 = 2; we can even construct it with compass and straightedge. But there is no rational number which satisfies the equation, even though the rationals have +, -, *, /, and <. For that matter, there are lots of numbers—e.g., 2^(1/3), π, e—that qualify as lengths but can’t be constructed by compass and straightedge. In general, if we have a normal, continuous function on an interval, and it’s negative at one end and positive at the other, then it should be zero somewhere in between—no line-jumping.

      The way we get that—pretty sure the only way we can get that—is as follows. Say we break our quantities into two sets P and Q. Every quantity is in exactly one of P or Q. Moreover P is downward closed: if x ∈ P and y < x, then y ∈ P also. This makes Q upward closed by default. Essentially we’ve split our line into two coherent halves.

      The intuition we appeal to—and by “we” I mean “originally Dedekind”—is that any such split should correspond to an actual quantity. That is, there should be some quantity x which is either the greatest element of P (and less than everything in Q), or the least element of Q (and greater than everything in P); and the split is taken to happen at x.

      So, for example, take an increasing but bounded sequence like x_n = 1 – 10^(-n), and take P = {x : x < x_n for some n} and Q = {x : x > x_n for all n}, and find the splitting point y. y is in Q, because if in P it would have to be the greatest element of P but still less than x_n for some n; but it is the *least* element of Q (that is, the least upper bound for {x_n}). We take y to be the limit of x_n. If there is no least upper bound, then there can be no limit. (There’s a similar idea for decreasing, bounded-below sequences; general sequences are trickier.)

      Let’s look at the sequence 1 – 10^(-n). Certainly 1 is an upper bound for this sequence. Is there a smaller one, say 1 – h for h positive? Well, if 1 – h is an upper bound, then so is 1 – 10h, since 1 – h ≥ 1 – 10^(-(n+1)) implies h ≤ 10^(-(n+1)) implies 10h ≤ 10^(-n) implies 1 – 10h ≥ 1 – 10^(-n); and this goes through for all n. And 1 – 10h < 1 – h. Thus (rewinding a bit), if 1 is not the least upper bound for x_n, then there is no least upper bound (every upper bound less than 1 can be shown not to be least, and upper bounds greater than 1 obviously don’t work). So either .9… = 1, or .9… doesn’t equal anything (or arithmetic is broken).

      So I guess I’ve come full circle on this issue. It’s true that any argument in math rests on certain assumptions about the context, but if we use infinite decimal expansions, we’ve internalized all those assumptions. We must either reject arithmetic, reject the .9… notation, or accept that .9… = 1.

      Chad Groft — February 5, 2010 @ 9:34 am

    39. Can you explain why such a subtraction wouldn’t be valid?

      Are there rules saying you can’t subtract some values?

      If you are worried that some people will argue against this, well you’re right, people who don’t want to be convinced won’t be, they’ll find any way they can to wriggle out of it.

      It is tricky yes, because the whole of Maths is abstract it doesn’t exist, there is no 1 that exists outside of our minds, there is nothing you can points to and say that is one, the idea of oneness is something we’ve invented to describe certain things.

      So it really is down to the abstraction people carry in their head for Maths, some people may not be aware that Maths is all in their head, what they can grasp is through a natural understanding of the basic abstract concepts of Maths, but when it comes to un-natural or super natural concepts it seems wrong because for them Maths always seemed different.

      Maths is nothing but a model or a system, a way of thinking about things that is useful, but it is just a model. Depending on how you use that model and what you consider to be its rules and limitations will depend on what you can and cannot believe.

      Maybe the hard bit is to make people think differently about Mathematics, from the very basic concepts.

      Maths models some certain real world domains really well, positive integers, basic fractions, addition. These are easy and simple to understand, it is easy to believe that Maths actually exists and is defined by these operations.

      Yet negative numbers have no real world analogues. What about bank accounts? Well problem is they don’t exist, they are abstract as well, in a bank there is no pile of your money, when you go overdrawn you don’t have a negative amount of money in a pile. The amount of money you have is an abstract representation of credit.

      Now many people can intuitively understand the abstract concept of negative numbers, and may never realise they are thinking, imagining and understanding such a concept. It seems natural because it is used so often by so many.

      However when you get to concepts of infinity it gets tricky, why? Because many people think Maths is real, it isn’t, it is entirely abstract and whilst it has concepts with comfortably match reality, it is not real. Now if you think of Maths as some real thing that exists then you have a problem, because no one can really grasp infinity. It is, you could say, the ultimate abstract concept. However because it is not something to see to perceive to touch taste etc. it doesn’t mean it is not a useful way to think, or a useful idea. It does however exist exactly the same amount as 1 or negative numbers, as a concept in our minds. But the ultimate effects of infinity are far more profound, perhaps only because they are not as comfortable or everyday as many mathematical concepts.

      This issue is one people have had a lot of problems accepting, irrational numbers, if you assume or expect that all numbers have to have exact values then you get stuck because that is not the case. Some numbers don’t even have exact values even though we call them constants, see PI or e we only have very close values to those, you could see the values we have as approaching the real value exactly as 0.999… approaches 1. Although we don’t know that PI or e are irrational, if they are then we will never have an exact value.

      0.999… comes to be used because we use numbers like 0.333… a number which cannot be satisfactorily displayed in decimal. Yet the decimal system has many benefits even if it cannot display some values satisfactorily, so we work with the system, and we have to accept that in this system 1/3 is represented as 0.333… and if we accept that then we have to accept that 0.999… is equal to 1. What is important that is these numbers are representations of the true value, not the value itself, because using an infinitely recurring number in calculations is pretty difficult.

      Ultimately what we write down on paper is not maths, it is a representation of Maths, the process that goes on in our heads, often it can be equivalent, and what you write are not just representing the absolute values but are the absolute values, but this is not always the case.

      You cannot write an absolute value in the decimal system to represent a third. How do you deal with this? We use a representation of a third, 0.333… We don’t use that value in calculations because we can’t because its not a value that can be written down. This applied to all values that cannot be represented absolutely in decimal we use a representations. And that is fine because Maths is not defined by what is written down. What we write down is a representation of the Maths in our heads.

      So in this way 0.999… isn’t 1, but it represents 1, and in that way it is 1. If you try and use Maths to prove that 0.999… equals 1 then you’ll may fail because you will be trying to use 0.999… as an absolute value when it is not.

      So does 0.999… equal 1? Well no, because 1 is an absolute value, and 0.999… is a representation of a value without an absolute value.

      So in maths, in the decimal system, 0.999… represents 1, 0.333… represents 1/3, we use these representations because decimal cannot give an absolute value we can use. Its not a problem because 0.333… or 1/3 is just a representation of a value which we understand in our head, we have other ways to use those values, and we often do, we can leave things in surd form, or we can accept close values, because we may not need high precision in calculations.

      The argument about 0.999… equalling 1 isn’t a mathematical argument it is a semantic argument about the way we represent Maths in a written form, as long as you understand the benefits and draw backs of using this it is not a problem.

      So back to the original point, is my subtraction valid? Not really because we aren’t using absolute values but representations, the calculation can never be finished because it goes off into infinity.

      However how much understanding does the person you are telling this to need to know, want to know? And does it matter anyway? Is the argument about 0.999… equal to 1 that significant in maths?

      Andrew — February 9, 2010 @ 4:10 am

    40. One simple comment. If we define a number system that allows 0.9999999… < 1 then that also implies that in the same number system the normal decimal expansion is not necessarily an equality. Or more precisly

      0.99999… 0.3333333 < 1/3. I'm not going to prove it, but the line of reasoning follows from the equality proof provided in a previous comment.

      I personally find this fascinating, because I'm currently learning about number theory and divisibility. And once you accept the entire set of real numbers most of those theorems go out the window. But if you accept infinitesimals, then you get em all back again.

      Ryan Chartier — February 21, 2010 @ 2:21 pm

    41. Could the experts comment on how this argument fits into this discussion:

      The formula for summing a geometric series is:

      1 + x + x^2 + x^3 + … = 1/(1-x)

      So

      .99999…. = .9(.1 + .01 + .001 + … )
      .99999…. = .9(1/(1-.1))
      .99999…. = .9(1.111…)
      .99999…. = 1

      Does this add anything, or does this just suppose the premise in question? And if so, what implications would this have for the formula of a geometric series?

      A student — February 23, 2010 @ 5:05 am

    42. @ Chad Groft… you said in #32, “since “infinitesimal separation” falls apart when we try to be precise and do arithmetic with it, this is an academic concern.”

      According to wikipedia, “The hyperreal numbers satisfy the transfer principle, which states that true first order statements about R are also valid in *R. For example, the commutative law of addition, x + y = y + x, holds for the hyperreals just as it does for the reals.”

      If the commutative laws (and others) truly hold, then what’s the problem? If we can add them and multiply them and do “arithmetic” with them, then they qualify as Number, correct?

      What am I missing? Have the hyperreals been given a rigorous treatment or not?

      Student — February 23, 2010 @ 9:41 am

    43. @41: You’re supposing the premise in question, namely that a limit exists. Try doing it with x = 2 and see what happens.

      @42: I wasn’t talking about the hyperreals. Those are well-defined and contain infinitesimals. It’s just not clear which infinitesimal 1 – 0.999… should be.

      Chad Groft — February 23, 2010 @ 3:01 pm

    44. If 0.999… = 1, then 1 is the sum of an infinite series. Are all (real?, rational?, integer?) numbers therefore likewise?

      Student — February 24, 2010 @ 8:25 am

    45. @43 Thanks. I really appreciate all you explanations…

      so am I to understand that we can do arithmetic with the hyperreals but not with the infinitesimals?

      I was under the impression that (one of) the point(s) you were making was that we could not apply the rules of arithmetic to the infinitesimals, or that they did not behave in a way that was consistent or something along those lines. Perhaps I was mistaken to think that if rigor had been applied to hypperreals then rigor had been applied to infintesimals?

      For me, the question of “do infinitesimals exist” in a manner that qualify them as “number” as defined by the commutative and other arithmeitc laws should settle the question of does 0.999… = 1.

      So, do infinitesimals rigorously qualify as numbers or not?

      Student — February 24, 2010 @ 9:05 am

    46. If 0.999… = 1, then 1 is the sum of an infinite series. Are all (real?, rational?, integer?) numbers therefore likewise?

      Well, yes, since every real number C can be represented as C/2 + C/4 + C/8 + …

      One thing you have to understand is, there’s no such thing as the infinitesimals. There are many contexts—for example, the rational numbers, the real numbers, the hyperreal numbers, the rational functions on one variable, the complex numbers—and infinitesimals exist (or don’t) within each context.

      Every real number (hence every rational number) is less than some natural number n (dependent on the real); so every positive real, no matter how “small”, is greater than 1/n for some natural number n. Thus infinitesimals don’t exist in Q or R; thus also the set {.9, .99, .999, …} has a least upper bound in Q and R, and it’s 1.

      On the other hand, consider the rational functions on one variable: all the fractions f(x)/g(x), where f and g are real polynomials (and g ≠ 0). These can be added, subtracted, multiplied, and divided (except by 0). We can also put an ordering < on them, for example by considering their behavior at +&infty;. Then the rational function 1/x is positive, but less than r for every positive real number r (because 1/x < r once x gets bigger than 1/r). We say that 1/x is an infinitesimal. Similarly the function x is greater than any real number, because once x gets large enough (i.e., greater than r), x > r. (Tautological, but still true.)

      The hyperreals are basically the above example on steroids. In addition to adding infinitely large (and infinitely small) numbers, we also import all sorts of higher-order structures from standard real-number theory. That lets us do analysis with infinitesimals, then translate the results back to real numbers. (Except nobody really bothers to anymore.)

      So yes, it’s possible to work with infinitesimals rigorously, if we’re in a context where they make sense. If you’re going to ask “[D]o infintesimals … qualify as numbers?”, I’ll have to ask “What kind of numbers?”

      What we’ve hashed out in the previous comments is, IF we are in an ordered field (that is, a context where +, -, x, ÷, and < are defined and behave as we expect), and IF the set {.9, .99, .999, …} has a least upper bound (which is the only sensible interpretation for .999…), THEN that least upper bound must be 1.

      We can have no infinitesimals, and say .99… = 1; we can have infinitesimals, and say .99… doesn’t resolve to anything; or we can drop the field property, and do some weird Dedekind-cut construction to have .99… resolve as just slightly less than 1. But we can’t have full arithmetic and .99… defined as something less than 1.

      Chad Groft — February 24, 2010 @ 3:40 pm

    47. @46 Thanks again. I remember having a sense from “studying” such things years ago that to “qualify as number” meant that the basic laws of arithmetic applied. Infinitesimals sound too messy to me.

      The problem with the Dedekind cut is that you have to let the process of adding the series finish before you cut. I would think Dedekind would simply point out that 0.999… is infinitely close to 1, which is another way of saying the “gap” is infinitely small, which is a pretty good definition of zero, is it not? If the gap is zero… no cut. The numbers are one and the same.

      To Kalid, I would say that this point kills all the intuitive attempts to inject a number in the gap. There can only be a gap at some discreet (location? moment? point?) in the series. And despite the fact that we can measure a gap at all such DISCREET points, this seems akin to the act of collapsing the wave function – by taking a measurement we have to stop the process!

      The most essential fact about an infinite series, however, is that the process NEVER stops. Any time we imagine a gap, we are imagining something discreet, which is to say we are imagining some OTHER number.

      It is as if we are saying, “add this to this to this to this and never stop, oh and when you are done tell me what the sum is so I can subtract from 1 and ‘measure the gap’”

      OK, tell you when I get there. Stand by! :)

      Student — February 25, 2010 @ 6:21 pm

    48. @Student, @Chad: Awesome insights! There’s so much I need to learn about the details of analysis. I think one of the biggest questions is “What does ‘0.999…’ really mean when someone asks about it?”

      Technically, we can interpret it as a limit, but it may not be what the student had in mind. They may be asking “What is the number closest to 1 but not one?” The traditional answer is “none — there is no such number, you are either 1 or not 1″ or alternatively “there is an entire class of small numbers infinitely close to 1 (appear like 1 to us, but are not the same at a different level of detail)” and then you explore the implications if that were possible (akin to exploring the idea that a square root of a negative number is possible).

      Our analysis of what 0.999… means may be like a linguist analyzing the sentence “I ain’t never gonna do that again”. Technically there’s a double-negative which means they _do_ want it again, but a step back realizes the intent of the statement. So there can be an impedance mismatch between what the asker is asking for and how the more knowledgeable answerer interprets it.

      That said, there’s 2 really interesting avenues: the analysis of the intuitive notion of infinitesimals (what is the person asking about?) and also the construction of other types of numbers (0.999… which may not be a “valid number”, etc.), which Chad summarized [i.e., your statement can be interpreted in the following ways...]. But I love the discussion! It’s a great chance for me to learn more about this topic.

      Kalid — February 26, 2010 @ 3:29 am

    49. @48 Kalid: Thanks for commenting on my blog! Your site inspired me to start my own. I have the mathematicians lament framed above my desk! You should also read David Foster Wallace’s book, “Everything and More.” It is all about this very topic. He is a talented author and communicator. His book is essential to this discussion for all the lay people out there who seek an intuitive sweep of the subject.

      And thank you Kalid for talking about this on your site, for this problem is the very core of which all of mathematics – and philosophy – revolves.

      I am by study a philosopher, not a mathematician, but if you boil it down, what is the difference? Just ask Bertrand Russell!

      Here is a thought for you that you can take to Pythagoras, Plato and Aristotle, who were the first giants to address these issues before we separated math and philosophy…

      I posit that all paradox comes from one source: the category mistake. We ask, “what color is 42?” and scramble for an answer, thinking we have disturbed the beast at the center of the universe when we have but made fools of ourselves.

      It was from Pythagoras that Plato got the idea of the Forms. But skip that. You can look it up. The point I am coming to is what Aristotle said in resolving Zeno’s paradoxes: there is the actual, physical world of 5 apples and then there is the abstract, potential world of the integer 5. Number. Form. Infinity. These are not concrete things. They are manifestations of the human mind. To ask. “are they real” is to make the category mistake, for in this question we transfer them from the category of potential abstract (integer) to the category of actual physical (apples).

      Similarly we can say things like:

      1: curiosity killed the cat.
      2: the world’s largest ball of twine is a curiosity
      3: the world’s largest ball of twine killed the cat

      This is akin to the category mistake. In philosophy we wrestle with the meaning of “to be,” “existence” and what it means to mean something. But we do not escape these problems in mathematics. We create the rigor as if we had changed professions and became lawyers, laying out the laws that prevent us from falling into these philosophical holes. But this is like saying that killing is wrong because it is illegal. In so doing, we simply avoid the real problem.

      Thus we make the category mistake. We treat the infinite like the discreet. We treat number like apple. We talk of points on line that take up no extension and then define a line as an extension, dense with points.

      Draw a circle, then draw another with twice the radius through the same center; smaller circle inscribed by larger. Now extend a line from this shared center so that the line extends through both circles, intersecting each at a point. If you were to rotate this line so that you cross each point of the inner circle you would also cross each point of the outer circle. Which is to say that there is a 1-to-1 correspondence between the “number” of “points” in each circle, despite the fact that the circumference, or “length” of one is greater than the other.

      In other words, given a line of any length, there are exactly the same count of “points” or “numbers” on this line as any other line, no matter what the “length.”

      This is set theory. Cantor please save us!

      Cantor says this infinity is larger than that infinity? This is how we are saved!?

      Abstraction of an abstraction of an abstraction… until we are integrating integrals and developing topological tautologies, will it ever end?

      We forget during all of this that we left the concrete world behind long ago. We have built a house of cards.

      But it works so well, you say! We have electricity! But what do we mean, “it works?” We mean the relationships work, which makes sense only insofar as we can apply these relationships to something concrete. The rules work, the equations work, but that does not mean that the abstract things we use as placeholders of the concrete are therefore real!

      Just because 5 of anything added to 5 of anything equals 10 of something does not mean that the integer 5 exists!

      And this is the crux of our conceptul problem with 0.999…

      It is not anything concrete. It represents a hypothetical idea. It is not real. What is real are concrete things and how they relate. Ideas merely help us do the relating, they are not that which we are to relate to!

      This is the category mistake. We ask, what color is 42?

      This is the source of all philosophical paradox and this case of the repeating decimal is one of the oldest, thorniest of them all.

      I find when I reach these impassable points that it helps to rename all my cliches. Instead of “number,” say “abstraction” for example. As in, “the abstraction, ‘0.999…’” or “the abstracton ‘1′”

      This helps remind me what number is. It is not 1 apple we are talking about. It is not something concrete we are discussing. It is not something actual that is causing us confusion. It is an idea (that we are trying to treat as if it were a concrete thing like an apple) that is causing us problems.

      When we talk of the “integers” we speak as if these abstractions are concrete, and thus we make the fundamental philosophical misstep, the category mistake.

      Student — February 26, 2010 @ 11:11 pm

    50. Yes, it is a truly mesmerizing question:

      “What is the number closest to 1 but not one?”

      Instead of trying to answer it, perhaps we should try to explain why it makes as much sense as asking:

      “What color is 42?”

      And what I mean, is does this question really make sense?

      By “number” do we mean “idea?”

      By “closest” do we posit some “unlimited divisibility of space”

      These questions are puzzling because the idea of a point and the idea of a line is puzzling, but no more so.

      When we imagine the continuum, we dream of things we cannot touch

      Student — February 26, 2010 @ 11:27 pm

    51. @Student: I can only encourage you to keep writing — you write very well and it’s a pleasure to read! I’m adding that book to my toread list :) .

      I like that distinction between what’s happening in the real world vs. what’s happening with our abstractions — are the questions even sensible? I love stepping back like this and questioning our basic assumptions about what an idea means. Often times we’re working in a framework which just makes it impossible to understand (my favorite example is assuming that a number (one abstraction) must be one-dimensional (another abstraction), while imaginary numbers throw those assumptions for a loop).

      I think the crux of the 0.999… issue may be if we allow the existence of another abstraction, the idea of infinitesimal numbers relative to our own.

      Kalid — February 27, 2010 @ 2:40 pm

    52. @51 Thank you very much. That is quite a compliment coming from you! I remember when I first realized that imaginary numbers were of “higher dimension.” That may have been the very thing that cemented my love of mathematics.

      Another interesting thought on your point of “the closest number” to any other number is that this question underscores the difficulty with an infinitely dense set. Because there are an infinite “number” of “numbers” between any 2 (real) numbers, can we ever even understand what it means to ask of one of these numbers, what the “next one” is? Or do we have to accept that the concrete concept of “next” has to be left down here on the ground while we ponder these ideas of the heavens?

      Lastly, in researching the nature of a repeating decimal, I have been reminded of the fact that a decimal is not a “number” but a special notation, or representation of a number! An abstraction on top of an abstraction. We started with those 5 apples and moved up to the abstract number 5, brought it back down to the world and pretended it was as concrete as those apples. Then we took a geometric series, went another level of abstraction up and invented decimal notation to make our abstraction less messy to write. We made a map of our map.

      We just keep forgetting that our maps are in fact maps! And in the case of the repeating decimal, a map of a map of a map.

      Somewhere along the way, I think we lose the ability to make certain concrete denotations of all these maps of maps.

      We are simply reminded of this when we ask a meaningless question like what color is 42, or what is the next real number.

      It is merely our own semantics that are failing us.

      At least that is my intuitive conjecture. Perhaps I should write all of this as a question. I would love to be shown right or wrong.

      Student — February 27, 2010 @ 4:02 pm

    53. wow a very lively discussion on this one. Haha looks like it’s really the simple yet profound problems that can get people from all backgrounds involved. Just the perfect combination of math, philosophy, reasoning, etc.

      @Kalid
      Yes please look into analysis and post some articles on it. The article on the imaginary unit as a rotation was great and now I’m not so scared of complex analysis. But analysis in general scares us students…

      Frank — February 27, 2010 @ 9:35 pm

    54. @52

      I think you have the point exactly.

      Maths is very interesting, as it is something we thought up inside our heads, I was thinking. Are we the only animals to have done this? I think not, consider the evolutionary benefits for an animal that can do this, if it can count, if it can estimate volume, or distances, by knowing this information it can make decisions. If its outnumbered it can run away, if its opponent is bigger it can run away, or smaller it can fight, it can tell if it can reach something or not.

      In this way we can see that an understanding of maths of some kind is present in many animals, but the understanding is natural, rather it is part of their way of experiencing and understanding the world.

      The difference with humans is that we have externalised this internal thought to a degree, rather than just have it as a tool that works to help us think and react in a subconscious way we have found a way to translate those ideas into a structure we can apply to a vast number of other situations. And a tool that is standardised between people.

      When you think about that is pretty impressive, whilst we all may think differently, and talk different languages mathematically we are all the same. (or similar, or are we? :D ) We have taken a basic fundament of consciousness and mapped it out.
      However the externalisation of this way of thinking is not the thing itself, it is a representation of our thought or mode of thought. And I guess here is where we get into philosophy. Simulation and Simulcra by Jean Baudrillard comes to mind, when you have a representation, an icon for something people eventually begin to focus on that as being not a representation but the actual thing. A representation is easier to deal with in the mind and so it comes to be a thing, the thing people think of. What is the meaning in the iconography of maths of 0.999… if you try to consider the meaning of a pure abstract idea as a real solid thing, considering a infinitely recurring number as an actual value such as an integer, how do you reconcile that with the rest of the iconography of maths which is more solid.

      The issue is one that affects more than this however as 0.999… is the tip of the iceberg as you move deeper into mathematics things become more abstract and as things start to become difficult to reconcile with the solid iconography of absolute numbers, you have to start accepting that the iconography of maths is not as solid as you thought, it is not absolute, which brings to mind Gödel’s work, essentially it was all about the validity of the iconography of the mathematic system, questioning its absoluteness. And the uproar it caused is basically a similar issue, the maths world had to reconsider the basic assumptions that maths was based on, instead of it being a solid system it is not, it can’t be proven absolutely. There are special cases and abstractions, abstractions based on abstractions. Trying to reconcile what you once thought as something solid and absolute with something which is not.

      Maybe if you want a nice safe place, thinking maths is absolute is great, you have a solid system to fall back on. You can ignore the fact it isn’t, to a degree, but in reality it’s not safe at all, it’s all about risks and reward, maths is dangerous, what assumptions should you make, should you accept, do they invalidate the system. Is the benefit of this way of thinking more useful than the problems the drawbacks create. Without a rigorous understanding of the limitations, assumptions, and fundamentals, you could fall into infinity, a circular argument, a paradox and never get out. Eventually you have to accept that Maths is a model, a system that we can use to model existence, but there is no such thing as a perfect circle, a perfect integer, or infinitely recurring or irrational numbers, at least not a meaningful representation in reality. The fuzzy world starts to encroach on the logical precise world.

      One thing I thought about when I was thinking about 0.999… how would such a result occur in maths, how could we get a results which gives that value? What possible inputs to lead to such an irrational output. Only irrational inputs. our mathematics is limited by precision as such the only time we can get a number like 0.999… is when we use other numbers like 0.333… and so on. The artefact of 0.999… is produced by the use of other equally irrational and non-absolute values, it isn’t a result of real world calculations, so to understand the answer we have to understand the inputs. So the question isn’t whether 0.999… is 1 but the question is, Is this the true question? In what cases is that answer received and why, it is not a real world answer, or maybe it is, can you add two rational numbers to get an irrational number? What two rational numbers do you add to make 0.999… What real world situations do we experience this as an answer? Or is it something which only occurs in abstract problems?

      If I get a result of 0.9999999999, I’ll call it 1 anyway because it is unlikely I need such precision. And ultimately 0.999… is even closer, or infinitely close to that value, not calling it 1 is just ridiculous, it is easy to get caught up in the belief of an absolute iconography of maths, but pull back, think, is 0.999… such a big deal, I don’t think it is, it is a storm in a teacup caused by people who are too busy trying to prove the iconography of absolute maths. Rather than examining maths itself where it exists and where it came from.

      Andrew — March 1, 2010 @ 6:26 am

    55. It’s funny listening to people talk at cross-purposes. Some of you sound like Nigel in Spinal Tap: “But these go to 11.” It’s what attracted me to contract law, legislation and eventually judicial review.

      And the art of communication, Chad, is to address your audience in a way that makes sense to that particular audience. Increasingly lengthy and arcane responses aren’t usually effective. See #31. It’s a good guess poor Nicole and Rick had no idea what you were saying. You can’t communicate with people by going over their heads.

      This is where Kalid shines. As he nicely makes clear, and as we eventually learn about most things in life, the answer depends. It’s why I become hyper-vigilant when an attorney asks the witness to answer “yes” or “no.” As though there were no shades of gray.

      At the risk of revealing myself to be the caveman that I am (aren’t we all looking for moments of clarity, a large black monolith that can help us advance?), what sits well with me is the idea that 0.999… and 1 are separate numbers. But they are so close to each other that there is no number between them. You can’t subtract 0.999… from 1 because the difference is, in my cave, undefined. So my number line isn’t perfectly continuous, and sometimes operations such as subtraction break down. But enough about me.

      Wheatgerm — March 3, 2010 @ 9:25 am

    56. @Wheatgerm: Well, it would be nice if there was a shallow end to this pool; but there just isn’t one. When you’re talking about what an argument is and what makes it valid, you have to think about all the explicit and implicit premises. (As someone who’s studied law, you probably understand that.)

      The rest of the response is to show that all those premises are necessary, by showing that the conclusion fails if any of the premises fail. The only way to do that is to construct counterexamples, and that takes a while. Perhaps my intent could have been made clearer.

      Kalid’s writing is in fact very clear, and I read this blog to improve my own exposition; but I’d rather express a true idea poorly than a false idea well.

      As for your (probably very common) idea that .999… and 1 are distinct numbers but have no numbers between them — where do you think (1 + .999…)/2 lies? If two real numbers are distinct, then their average must lie strictly between them.

      Chad Groft — March 3, 2010 @ 2:36 pm

    57. I should moderate that last paragraph.

      Your “number line” sounds a lot like the construction I outlined in comment 32, where one gets the sort of resolution you talk about at the expense of being able to do arithmetic. If we’re talking about real, physical magnitudes, though, we want the “common” real number line.

      Did comment 46 make any sense?

      Chad Groft — March 3, 2010 @ 2:43 pm

    58. I like this view:
      let X=0.999…
      then 1+X=1.999…
      also X+X=1.999…
      so 1+X=X+X and thus 1+X UNLESS we want to junk the rules of arithmetic that we like to use.

      Aaron — April 11, 2010 @ 7:17 am

    59. Okay, let’s say the error margin concept is true.
      Then I might as well say that a particle has no mass, since we can’t possibly measure it – nor has it any volume since we can’t measure that either.
      I don’t think that makes it matematically correct to assume things, based on the fact that we can’t measure it.
      Hence, 0.999′ will never equal 1 either. It’s convenient for mathematicians, no doubt – but that’s about it! c”,)

      Bruno — April 27, 2010 @ 7:00 pm

    60. Oh, and by the way…haileris wrote in #11:

      1/3 (one third) can be represented by 0.333…
      If you take each thirds and add them up (0.333.. + 0.333… + 0.333…) they add up to 1.0, not 0.999…

      This argument assumes falsely that 1/3 can be represented by 0.333′.
      The flaw in this one is, that 0.333′ is NOT 1/3, only an approximation(!)

      Bruno — April 27, 2010 @ 7:11 pm

    61. I don’t think it should be a question of wether 0.999… = 1, but a question of wether 0.333… = 1/3.

      Nath — May 13, 2010 @ 4:51 pm

    62. The color of 42 is Kansas City. I thought everyone knew that!

      Largo — June 24, 2010 @ 4:30 am

    63. Yes, 0.999… = 1. OK, fine, but will someone please tell me what the next real number is???

      A Student

      Student — July 5, 2010 @ 9:02 pm

    RSS feed for comments on this post. TrackBack URI

    Leave a comment

    Have a question? Know an explanation that caused your own a-ha moment? Write about it here.


    		Subscribe (RSS or Email)
    Get new articles by email:
    Get the Math, BetterExplained ebook for clear insights into key math concepts.

    Get the ebook
    About (Contact Kalid)
    Learning shouldn't hurt. Let's share the insights that made difficult ideas click. Read more...
    Popular Articles | All Posts
    Starting Ruby on Rails: What I Wish I Knew
    Easy Permutations and Combinations
    A Visual, Intuitive Guide to Imaginary Numbers
    Mental Math Shortcuts
    How To Optimize Your Site With HTTP Caching
    Speed Up Your Javascript Load Time
    A Visual Guide to Version Control
    An Intuitive Guide To Exponential Functions & E
    How To Optimize Your Site With GZIP Compression
    Demystifying the Natural Logarithm (ln)
    Categories
    Business
    General
    Guides
    Math
    Calculus
    Vector Calculus
    Observations
    Personal Development
    Programming
    Web

    Like it? Try All articles, RSS Feed or Email Subscription | Idea or suggestion? Contact me
    copyright © 2009 Kalid Azad