Intuition For The Law Of Sines

The Law Of Sines is something I memorized in a class once, but didn’t internalize:

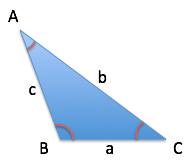
$\displaystyle{\frac{\sin(A)}{a} = \frac{\sin(B)}{b} = \frac{\sin(C)}{c} }$

Ok, that’s a neat connection, and maybe we can prove it by drawing some right triangles (of course) and re-arranging terms.

But what does it mean?

Rather than the Law of Sines, think of the Law of Equal Perspectives:

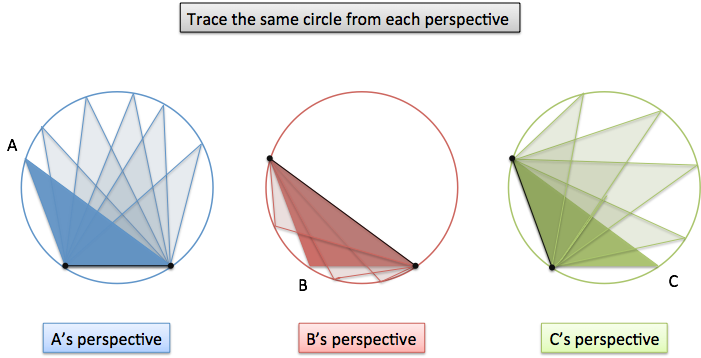
Each angle & side can independently find the circle that wraps up the whole triangle. This connection lets us start with one angle and work out facts about the others.

Analogy: Kids Describing A Monster

I occasionally frighten the neighborhood children by unchaining the mutant gorilla in my front yard.

The kids run screaming, telling different stories of what they’ve seen:

“Alice claims the monster was 20 feet tall, but we all know she exaggerates by doubling. And Billy’s a bit of a crybaby, and said it was 30 feet tall. Charlie’s fairly no-nonsense and said the beast was exactly 10 feet high.”

If we know a kid’s “exaggeration factor” and the size they claim, we can deduce the true size of the monster. (Furious George has a name, you know.)

Even better, we can predict what other kids might have said: If Alice claimed it was 40 feet, what would Charlie have said?

Triangles And The Monster Circle

What do kids running from monsters have to do with triangles? Well, every triangle is trapped inside its own Monster Circle:

Whatever triangle we draw, there’s some circle trying to gobble it up (technically, “circumscribe it”). Try this page to explore an example on your own.

Now here’s the magic: just knowing a single angle and its corresponding side, we can figure out the Monster Circle.

Here’s how. Let’s say we have a triangle like this:

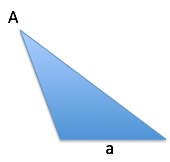
We don’t know anything except the angle $A$ (call it 30 degrees) and the length of side $a$ (call it an inch).

First off: is this the correct drawing of the triangle? Probably not! We don’t know the other sides, so this is equally valid:

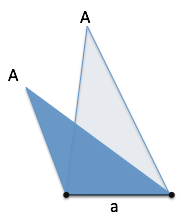
It still has the same angle ($A$ = 30 degrees) and the size of the base hasn’t changed (still one inch).

What if we start drawing more possibilities?

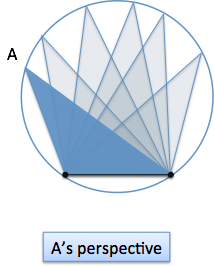
Whoa. From $A$’s point of view all the possible triangles that have “$A$=30 degrees, $a$=1 inch” are on this circle. Whatever B and C end up being, they need to pick an option from this circle.

Similarly, we can argue this from the other perspectives:

We can lock down angle $B$ and side $b$, and trace out a circle of possibilities
We can lock down angle $C$ and side $c$, and trace out a circle of possibilities

This is the meaning of the Law of Sines: each angle unknowingly generates the same circle as the others.

(How do we prove, not just see that the possibilities lie on a circle? That’s the Inscribed Angle Theorem, for another day.)

Calculating The Actual Size

We’ve figured out that there is a Monster Circle, now let’s see how big it is. Um… how?

Remember, we can slide around the circle and keep $A$ (30 degrees) and $a$ (1 inch) the same. So let’s slide until we make a right triangle:

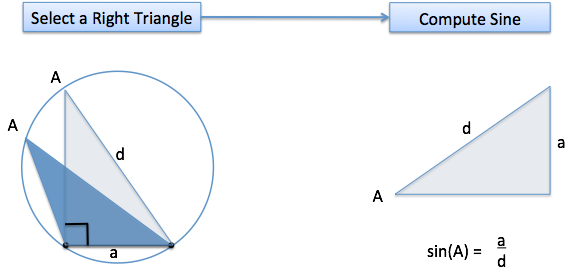
Ah! Now we can use sine. Remember that sine is the percentage height compared to the max possible. The max possible height is the full diameter ($d$) of the Monster Circle.

(Why is a 90-degree angle across from the full diameter? Draw a square inside the circle, touching the sides. It must be symmetric, the diagonals pass through the center along the diameter, and are opposite a 90-degree angle.)

With a little re-arranging, we get:

$\displaystyle{ \frac{a}{\sin(A)} = d }$

Using the same logic for the other sides, we get:

$\displaystyle{ \frac{a}{\sin(A)} = \frac{b}{\sin(B)} = \frac{c}{\sin(C)} = d }$

In a way, $\sin(A)$ is the “exaggeration factor” that converts the size the angle measured ($a$) to the full diameter ($d$). Each angle is a different kid, and some really misjudge the size of the full circle based on what they see. (90-degrees is right on target.)

Practice Problem

In our example above, $A$ is 30 degrees and $a$ is 1 inch.

We can calculate the diameter pretty fast. First, we get the sine:

$\displaystyle{\sin(30) = 0.5}$

That means our length $a$ is 50% of the max height, so the full diameter must be 2 inches.

This isn’t enough to figure out the triangle by itself. Let’s say angle $B$ comes along and says it is 45 degrees. How long is $b$?

Well,

$\displaystyle{\sin(45) = .707}$

which means that $b$ is .707 of the max diameter. Therefore,

$\displaystyle{ b = .707 \cdot \text{2 inches} = \text{1.414 inches}}$

Previously, I would plug numbers into the Law of Sines formula and chug away algebraically. Now I can think in terms of the Monster Circle: “Ok, I have the max diameter. I take the sine, and get the fraction of the max diameter for that side.”

Most books write the formula with sin(A) in the numerator. It might read better “Sine A over A” but it distorts the conclusion that $\frac{a}{\sin(A)}$ is the size of the circle.

Put the concept in your own words. The “Law of Sines” is a generic description of what’s in the formula, but the “Law of Equal Perspectives” explains what it means:

All parts of the triangle have a perspective on the whole
Sine is the “exaggeration factor” that scales up an individual side to the full diameter. (Sine is the percentage of the max possible, and we divide by it.)

Happy math.

Appendix: Obtuse Angles

Technically, because $B$ is over 90 degrees, we can’t ever spin it and have either $A$ or $C$ be a right angle (if we could, the triangle would have over 180 degrees).

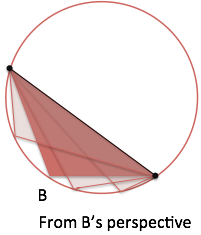
What to do? Realize the 180-degree complement of $B$ (call it $B\star$) acts like a stand-in on the other side:

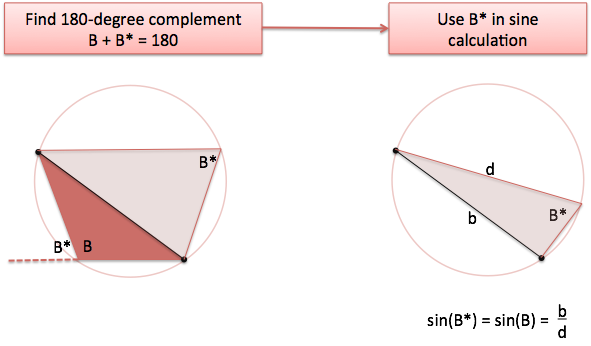
$B \star$ has the same sine as $B$, which should make sense: they both point upwards along the same trajectory. To help us sleep better at night, we start with $B \star$ in the right-angle setup:

$\displaystyle{\sin(B \star) = \sin(B) = \frac{b}{d} }$

and get to the same conclusion as before. Phew.

However, the fact that $B$ and $B\star$ can be swapped can lead to problems.

If I have a triangle where I know $A$ (30 degrees) and $a$ (1 inch), and then say $b$ is 1.5 inches, what can you deduce?

The max diameter is 2 inches as before, so

$\displaystyle{\sin(B) = \frac{1.5}{2} = .75}$

Unfortunately, there are two angles with that sine value: a calculator says $\sin^{-1}(.75) = 48$ degrees, but $180 – 48 = 132$ degrees would work too (more details).

Also, the triangle may not be possible given a hypothetical scenario. If I say $b$ is 3 inches, you know something’s amiss. The max diameter was already calculated to be 2. Even a 90-degree angle, the best possible, could only have a side of 2 inches.

ADEPT Summary

ADEPT Topic	Law of Sines
Analogy	Imagine kids describing the same monster with varying degrees of exaggeration.
Diagram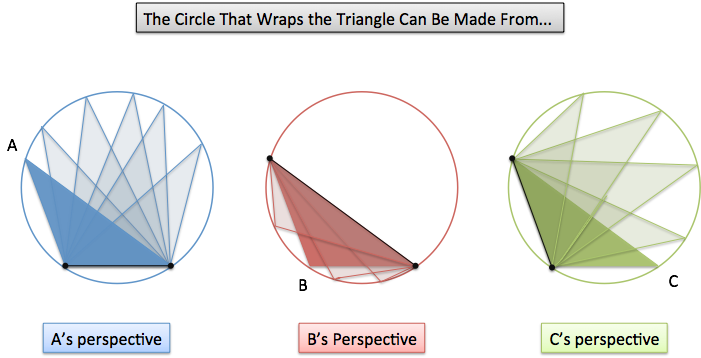
Example	Suppose $A$=30 and $a$=1 inch. Since $\sin(A) = 0.5$, the Monster Circle is 1 / 0.5 = 2 inches wide. Given another angle, I can figure out the length of its side. If $B$ = 45 degrees, then side $b$ takes up $\sin(45) = .707$ of the diameter, and is 1.414 inches.
Plain-English	Any angle + side can deduce the size of the wrapping circle.
Technical	$\displaystyle{\frac{a}{\sin(A)} = \frac{b}{\sin(B)} = \frac{c}{\sin(C)} = \text{diameter of circle} }$