Easy Trig Identities With Euler’s Formula

Trig identities are notoriously difficult to memorize: here’s how to learn them without losing your mind.

Starting from the Pythagorean Theorem and similar triangles, we can find connections between sin, cos, tan and friends (read the article on trig).

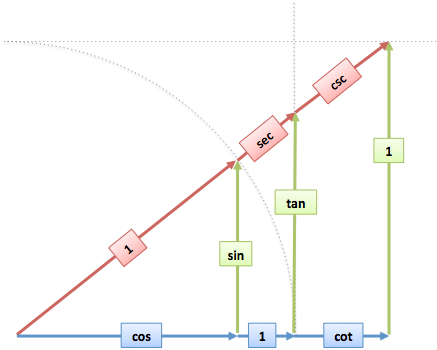
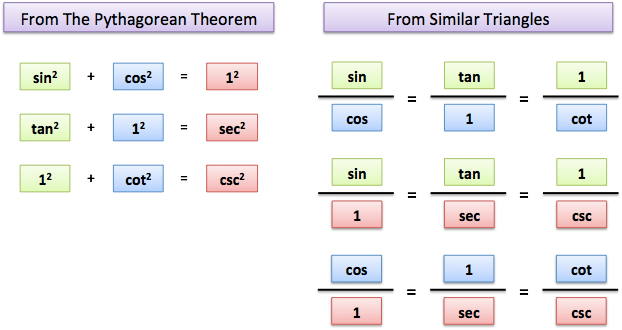
Can we go deeper? Maybe we can connect sine with itself (sin-ception). In math terms, we’re looking for formulas like this (full cheatsheet):

Instead of memorizing these bad mamma jammas, let’s learn to draw the formulas. Euler’s Formula makes it easy.

Connections In Algebra

In algebra, we study relationships like this:

Working out $17^2$ directly is cumbersome. But we can simplify it to:

In the computer era, sure, we can just crunch $17^2$ directly. The important aspect is realizing that $(a + b)^2$ can be broken into simpler ingredients: $a^2, b^2, a, b$. This is useful in factoring, simplifying equations, and so on.

Connections In Trig

Let’s turn trig into plain English. What does this mean?

Remembering that sine is “height (as a percentage of max)”, this equation asks: If we add two angles, what is their total height?

A quick guess might be to combine the individual heights:

It looks clean, but isn’t quite right. If we keep adding up angles, their height increases until the max (100%), then starts decreasing.

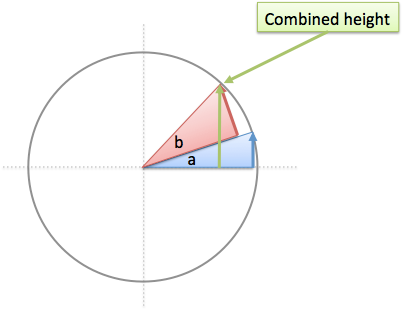
The relationship between angle and height can’t be simple addition.

Now here’s the weird thing: I can draw what the new height should be (It’s right there!), but I can’t turn my drawing into an equation.

Or can I?

Drawing With Euler’s Formula

Euler’s Formula lets us create a circular path using complex numbers:

Crucially, multiplying complex numbers performs a rotation. Aha! We can use Euler’s Formula to draw the rotation we need:

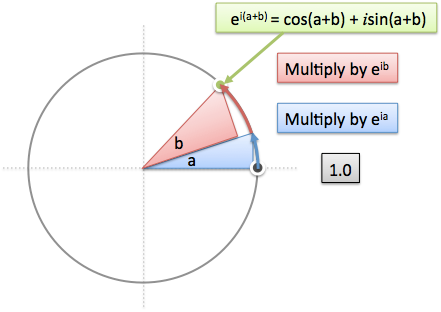
• Start with 1.0, which is at 0 degrees.
• Multiply by $e^{ia}$, which rotates by $a$.
• Multiply by $e^{ib}$, which rotates by $b$.
• Final position = $1.0 \cdot e^{ia} \cdot e^{ib} = e^{i(a+b)}$, or 1.0 at the angle (a+b)

The complex exponential $e^{i(a+b)}$ is pretty gnarly. Just like breaking apart $17^2$, let’s multiply out the pieces:

Now we’re talking! This version easily separates the horizontal position (real component) and vertical position (imaginary component):

• Combined height: $ \sin(a + b) = \sin(a)\cos(b) + \sin(b)\cos(a) $
• Combined width: $ \cos(a + b) = \cos(a)\cos(b) – \sin(a)\sin(b) $

Boom: two annoying-to-remember trig identities in a single computation. Not a bad deal.

Understanding The Equation

Now that we’ve found the equation, let’s grok its meaning. When we add the heights, here’s what’s happening:

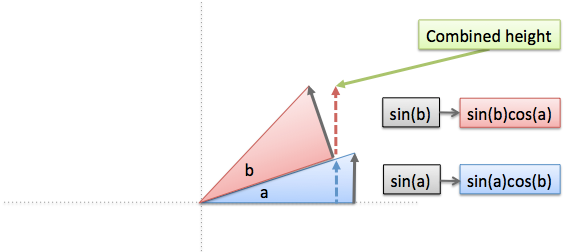
• The full height of the blue triangle ($\sin(a)$) can’t be used, since the red triangle doesn’t extend as far. (Why? When we add angle $b$, we’re moving at a steeper angle with the same hypotenuse. We gained vertical distance and lost horizontal distance.) We’re effectively “sliding back” $\sin(a)$, reducing it by a factor of $\cos(b)$.
• The full height of the red triangle ($\sin(b)$) can’t be used either, since it’s at an angle. We’re “turning” $\sin(b)$, reducing it by a factor of $\cos(a)$.

Remember that sine and cosine are percentages. In this case,

or

Sure, we would like to get the full height of each triangle. But from the diagram, we see $a$ slides back and $b$ is twisted, so height we actually get is reduced. Think of each cosine as a tax on your height, reducing the amount you take home. (Have a height of .90? That’s nice, Papa Cosine will let you keep 75%. Pay up the rest, sucka!).

Now, what happens for small angles, like $\sin(.01 + .02)?$

We could plug and chug this. But I’m guessing the result is about:

Why? My mental diagram for small angles is this:

There’s no perceptible difference between the ideal heights ($\sin(a)$ and $\sin(b)$) and the “taxed” versions ($\sin(a)\cos(b)$ and $\sin(b)\cos(a)$).

• For tiny angles, $\sin(a + b)$ is a vertical line. It barely loses any height due to the parts sliding or twisting.
• For small angles, cosine (the percent we keep), is close to 100%. We’re keeping the vast, vast majority of the height we have.
• $\sin(x) \sim x$ is a common approximation for small angles (often used in Calculus). Essentially, it says $\sin(x)$ is a line for a brief time period. For small angles, $\sin(a + b) \sim \sin(a) + \sin(b) \sim a + b$.

For cosine, we have a similar diagram:

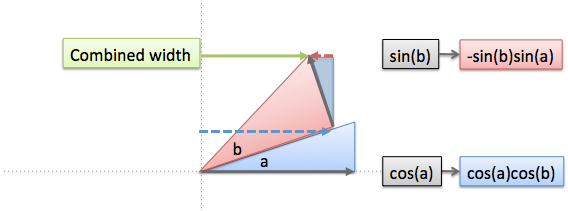
• This time, the conversion factor matches up (cosine with cosine, sine with sine).
• The full width of the first triangle ($\cos(a)$) gets scaled down to match the width of the second.
• The sine term is negative since it pushes us backwards, reducing our height. We can use similar triangles to extract out this piece.

I’m not typically thinking about the parts in the diagram, though it’s nice to see how they work a few times. If you just need the trig identity, crank through it algebraically with Euler’s Formula.

Why do we care about trig identities?

Good question. A few reasons:

1. Because you have to (the worst reason). Many trig classes have you memorize these identities so you can be quizzed later (argh). You don’t need to memorize them, you can work out the formula in about a minute. Save your precious brain space for something else.

2. We can now “factor” trig functions into simper parts. We can now separate sine into smaller parts, which is useful in Calculus.

For example, to find the derivative of sine, we need:

and we let $dx$ go to zero. This is tricky to work on directly, but using the $\sin(a + b)$ formula we have

As $dx$ goes to zero, $\cos(dx) = 1$ (zero angle is full width), so we have:

And as $dx$ goes to zero, $\sin(dx)$ and $dx$ become equal:

Plugging this in, we get $\cos(a)$ as the derivative of $\sin(a)$. Phew! Working with trig functions isn’t always easy, but at least it’s manageable.

3. It’s computationally efficient. If you’re doing a computer graphics, and frequently calculating sine/cosine (for dot products let’s say), trig identities are useful shortcuts. In the past, these identities were used similar to log tables to make hand-done calculations easier.

4. Math is about seeing connections. Because trig functions are derived from circles and exponential functions, they seem to show up everywhere. Sometimes you simplify a scenario by going from trig to exponents, or vice versa.

5. Deepen your knowledge of Euler’s Formula. Master Euler’s formula and you’ve mastered circles. And from there, the world! (Editor’s note: Kalid’s pinky appears to be affixed to his mouth. We’re working on it.)

See, Euler’s formula lets us draw a circle and read off a position. That’s amazing! We can avoid a lot of painful geometry with a few multiplications. If you’re doing any advanced math, letting Leonhard Euler deep into your soul is well worth it. He’s good company.

That’s it for today. Happy math.

Appendix: Resources and Extended Formulas

You can modify the parameters $a$ and $b$ to create new identities.

Subtraction formula: replace b with -b

Double-angle formula: replace b with a

Half-angle formula: replace and solve

Start with the double-angle formula and solve for $\sin(a)$, which is half the angle used in $\sin(2a)$. Trig without tears (a great resource and name) has more details:

http://brownmath.com/twt/double.htm

A few other references I found helpful:

• http://www.tc.umn.edu/~nydic001/docs/unpubs/Eulers_Formula_and_Trig_Identities.pdf
• https://www.wyzant.com/resources/lessons/math/trigonometry/eulers-formula-trig-identities
• http://www.ctralie.com/Teaching/Euler/
• http://kunklet.people.cofc.edu/MATH220/euler.pdf

Other Posts In This Series

1. How To Learn Trigonometry Intuitively
2. Easy Trig Identities With Euler's Formula
3. Intuition For The Law Of Cosines
4. Intuition For The Law Of Sines
5. How to Learn Trig Derivatives