Learn Difficult Concepts with the ADEPT Method

After a decade of writing explanations, I’ve simplified the strategy I use to get new concepts to click.

Make explanations ADEPT: Use an Analogy, Diagram, Example, Plain-English description, and then a Technical description.

Here’s how to teach yourself a difficult idea, or explain one to others.

Contents

Analogy: What Else Is It Like?
Diagram: Engage That Half Of Your Brain
Example: Let Me Experience The Idea
Plain-English Description: Use Your Own Words
Technical Description: Learn The Formalities
The Mental Checklist
Modifying the Learning Order
The Goal: Explanations That Actually Work
Bonus: BE ADEPT
Appendix: ADEPT Summaries
Other Posts In This Series

Analogy: What Else Is It Like?

Most new concepts are variations, extensions, or combinations of what we already know. So start there!

In our decades of life, we’ve encountered thousands of objects and experiences. Surely one of them is vaguely similar to this new topic and can be the starting point.

Here’s an example: Imaginary numbers. Most lessons introduce them in a void, simply saying “negative numbers can have square roots too.”

Argh. How about this:

Negative numbers were distrusted until the 1700s: How could you have less than nothing?
We overcame this by realizing numbers could exist on a number line, allowing us to move forward or backward from zero.
Imaginary numbers express the idea that we can move upwards and downwards, or rotate around the number line.

Instead of just going East/West, we can go North/South too – or even spin around in a circle. Neat!

Analogies are fuzzy, not 100% accurate, and yet astoundingly useful. They’re a raft to get across the river, and leave behind once you’ve crossed.

Diagram: Engage That Half Of Your Brain

We often think diagrams are a crutch if you aren’t macho enough to directly interpret the symbols. Guess what? Academic progress on imaginary numbers took off only after the diagrams were made!

Favor the easiest-to-absorb explanation, whether that comes from text, diagram, or interpretative dance. From there, we can work to untangle the symbols.

So, here’s a visualization:

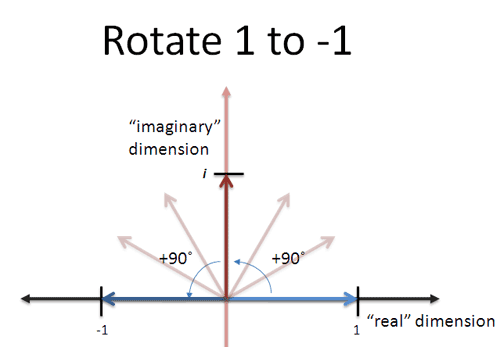
Imaginary numbers let us rotate around the number line, not just move side-to-side.

Starting to get a visceral sense for what they can do, right?

Half our brain is dedicated to vision processing, so let’s use it. (And hey, maybe for this topic, twirling around in an interpretative dance would help.)

Example: Let Me Experience The Idea

Oh, now’s our chance to hit the student with the fancy terminology, right?

Nope. Don’t tell someone the way things are: let them experience it. (How fun is hearing about the great dinner I had last night? The movie you didn’t get to see?)

But that’s what we do for math. “Someone smarter than you thought this through, found out all the cool connections, and labeled the pieces. Memorize what they discovered.”

That’s no fun: let people make progress themselves. Using the rotation analogy, what happens after 4 turns?

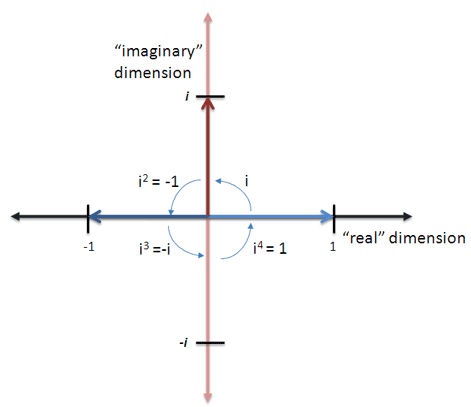
How about 2 turns? 4 turns clockwise?

Plain-English Description: Use Your Own Words

If you genuinely experienced an idea, you should be excited to describe it:

Imaginary numbers seem to point North, and we can get to them with a single clockwise turn.
Oh! I guess they can point South too, by turning the other way.
4 turns gets us pointing in the positive direction again
It seems like two turns points us backwards

These are all correct conclusions, just not yet written in the language of math. But you can still reason in plain English!

Technical Description: Learn The Formalities

The final step is to convert our personal understanding to the formal notation. It’s like sharing a song you’ve made up: you can hum it to yourself, but need sheet music for other people to use.

Math is the sheet music we’ve agreed upon to share ideas. So, here’s the technical terminology:

We say i (lowercase) is 1.0 in the imaginary dimension
Multiplying by i is a 90-degree counter-clockwise turn, to face “up” (here’s why). Multiplying by -i points us South
It’s true that starting at 1.0 and taking 4 turns puts us at our starting point:

$\displaystyle{1 * i * i * i * i = 1 }$

And two turns points us negative:

$\displaystyle{1 * i * i = -1 }$

which simplifies to:

$\displaystyle{i^2 = -1}$

$\displaystyle{i = \sqrt{-1}}$

In other words, i is “halfway” to -1. (Square roots find the halfway point when using multiplication.)

Starting to get a feel for it? Just spitting out “i is the square root of -1” isn’t helpful. It’s not explaining, it’s telling. Nothing was experienced, nothing was internalized.

Give people the chance to make an idea their own.

The Mental Checklist

I used to be satisfied with a technical description and practice problem. Not anymore.

ADEPT is a checklist of what I need to feel comfortable with an idea. I don’t think I’ve actually learned a topic unless I have a metaphor that ties everything together. Here’s a few places to look:

Analogy – ?
Diagram – Google Images
Example – Khan Academy for practice problems
Plain-English – Forums like /r/math or Math Overflow
Technical – Wikipedia or MathWorld

Unfortunately, there aren’t many resources focused on analogies, especially for math, so you have to make your own. (This site exists to share mine.)

Modifying the Learning Order

It seems logical to assume we can present facts in order, like transmitting data to a computer. But who actually learns like that?

I prefer the blurry-to-sharp approach to teaching:

Start with a rough analogy and sharpen it until you’re covering the technical details.

Sometimes, you need to untangle a technical description on your own, so must work backwards to the analogy.

Starting with the technical details:

Can you explain them in your own words?
Can you solve an example problem, describing the steps in your own words?
Can you create a diagram that represents how the concept fits together for you?
Can you relate the concept to what you already know?

With this initial analogy, layer in new details and examples, and see if it holds up. (It doesn’t need to be perfect, but iterate.)

If we’re honest, we’ll admit that we forget 95% of what we learn in a class. What sticks? A scattered analogy or diagram. So, make them for yourself, to bootstrap the rest of the understanding as needed.

In a year, you probably won’t remember much about imaginary numbers. But the quick analogy of “rotation” or “spinning” might trigger a flurry of recognition.

The Goal: Explanations That Actually Work

I’m wary of making a contrived acronym, but ADEPT does capture what I need to internalize a new concept. Let’s stop being shy about thinking out loud: does a fact-only presentation really work for you? What other components do you need? I have a soft, squishy brain that needs the connecting glue, not just data.

Scott Young uses the Feynman Technique to explain concepts in everyday words and work backwards to an analogy and diagram. (Richard Feynman was a world-class expositor and physicist, and one of my teaching heroes.)

Tom Roth wrote a nice summary for ADEPT, Feynman Technique, and others.

Beyond any technique, raise your standards to find (or create) explanations that truly work for you. It’s the only way to have concepts stick.

Happy math.

Bonus: BE ADEPT

“BE” is a nice prefix for the style to use when teaching:

Brevity is beautiful.
Empathy makes us human. Use your natural style, relate to common experience, and anticipate questions in your explanation.

I’ve yet to complain that a lesson respected my time too much, or related too well to how I thought.

Appendix: ADEPT Summaries

ADEPT is like a nutrition label for an explanation: what are the key ingredients?

Concept	Euler’s Formula
Analogy	Imaginary numbers spin exponential growth into a circle.
Diagram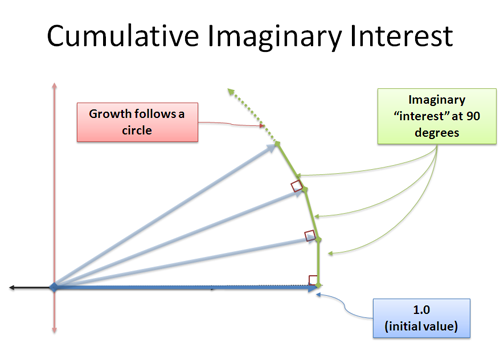
Example	Let’s figure out the value of `3^i`. (It’s on the unit circle.)
Plain-English	Raising an exponent to an imaginary power spins you on the unit circle. The same destination can be written with polar (distance and angle) or rectangular coordinates (real part and imaginary part).
Technical	$\displaystyle{e^{ix} = \cos(x) + i\sin(x)}$

Concept	Fourier Transform
Analogy	Like filtering a smoothie into ingredients, the Fourier Transform extracts the circular paths within a pattern.
Diagram	Smoothie being filtered: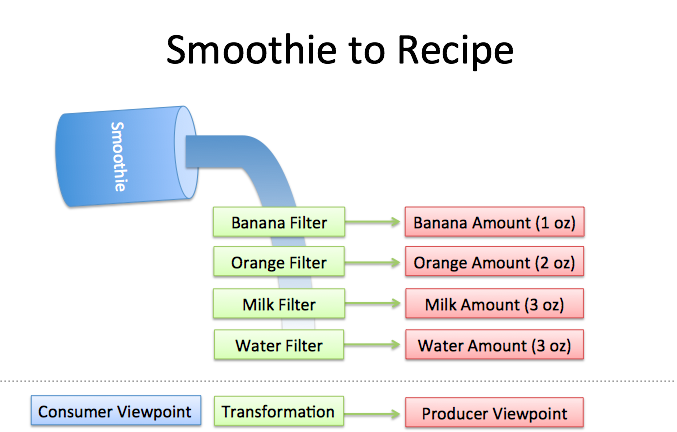
Example	Split the sequence `(4 0 0 0)` into circular components: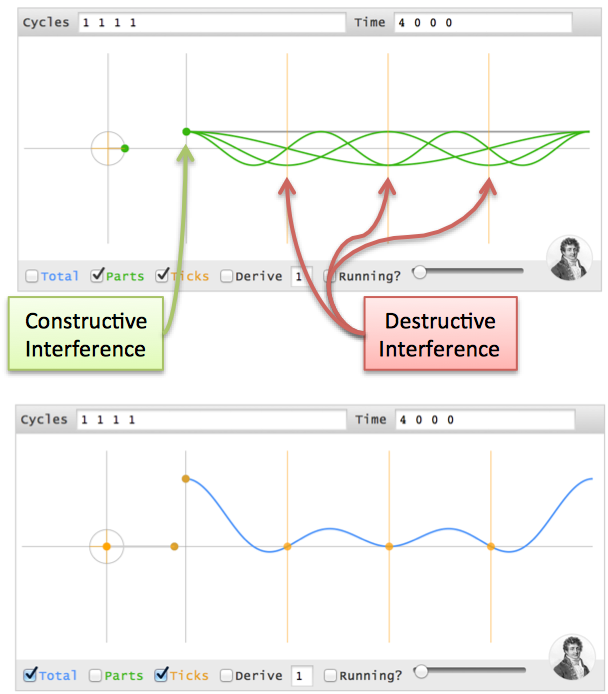
Plain-English / Technical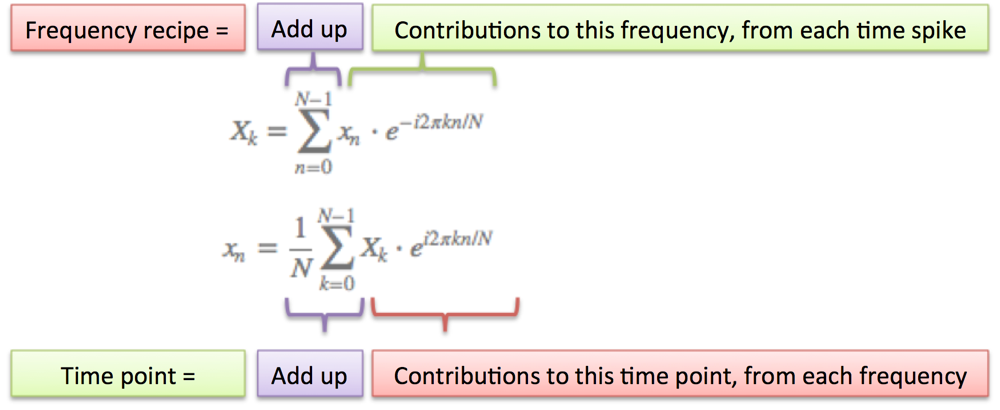

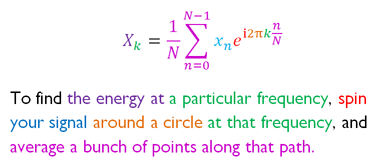
Concept	Distributed Version Control
Analogy	Distributed Version Control is like sharing changes to a group shopping list with your friends.
Diagram / Example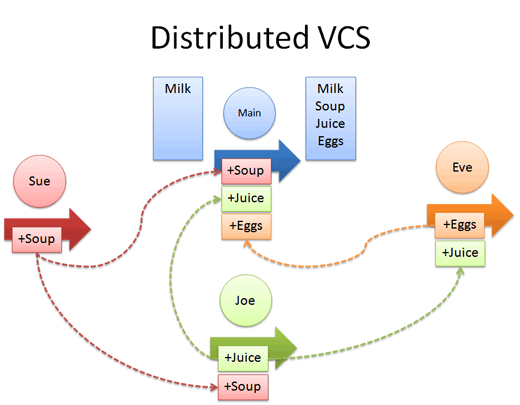
Plain-English	We check out, check in, branch, and share differences (“diffs”).
Technical	`git checkout -b branchname` `git diff branchname`

Combine ingredients with your own style. Steps might merge, but shouldn’t be skipped without a good reason (“Zombies coming, no time for biochem, use this serum for the cure.”). The site cheatsheet has a large collection of analogies.