You’re reading this, so I’ll assume your English is pretty good. What’s wrong with these phrases?
- Old little lady
- Red big dog
- Vietnamese spicy food
Do you have a logical reason for why they sound strange? Or are they just off?
You probably didn’t think, “In 3rd grade I mastered the Royal Order of Adjectives:
- Determiner
- Observation
- Size
- Shape
- Age
- Color
- Origin
- Material
- Qualifier
… and upon applying them, noticed several errors. Old little lady is incorrect because rules #3 and #5 are swapped — a childish mistake, really. The next…”
Ugh. Describing Gran Gran isn’t a logic puzzle. But guess what students learning English are taught?
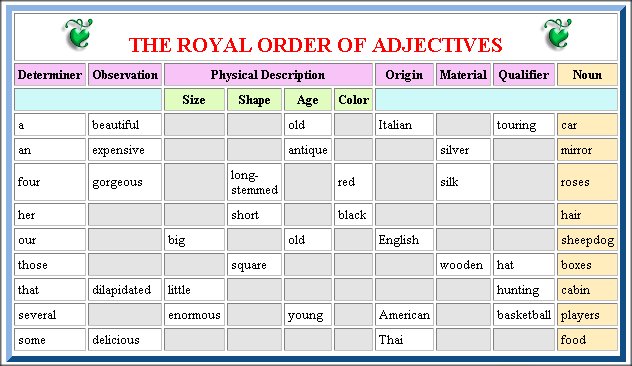
Even as a native speaker, could you construct this chart? Is this how you’d teach someone English?
The Adjective Fallacy is trying to learn by mastering the formal rules. Just because a concept can be rigorously defined doesn’t mean we should study it that way.
We didn’t become good at English by studying a chart: we developed an ear for the language and know how it should sound. And “old little lady” sounds off.
Similarly, getting good at math doesn’t mean marching through a gauntlet of rules on every problem. It’s having a native speaker’s feeling about what works or doesn’t.
“303 x 13 = 5074” looks strange, but not because we computed the left-hand side. It’s weird because odd numbers can’t multiply to become even (intuition). The last digit of the result should be 3×3= 9. 5074 is too large, since 300 x 10 (similar numbers nearby) is only 3000. Our Spidey Sense is blaring that the computation looks wrong.
My learning goal is knowing enough to make rough predictions on my own. I want a horse sense for algebra, calculus, trig, and even imaginary exponents, without scurrying off to apply an equation.
Rules aren’t inherently bad: they summarize, resolve ambiguous cases, and help us practice our weak spots. The question is how much to use them when starting off.
Learn enough rules to get started – don’t attempt to master them from the outset. See examples in a larger context and let the pattern-matching machinery of your brain get to work.
Learning Math
Math is a language too. Here’s a gut check: Would my current math study technique have helped me learn English?
If an English class spent a month on the adjective chart we’d have a talk with the teacher. But a Calculus class that spends weeks on the formal theory of limits is typical. Can we admit that studying this much detail, this early, doesn’t build fluency?
Pondering that question made me realize I had large gaps in trigonometry and calculus. I could only describe concepts using the adjective chart I’d memorized with a furrowed brow. (I’ll describe my grandma, just give me a minute!)
Enough was enough: embrace approaches that actually help you, like seeing the big picture first. In Calculus, that might mean seeing an integral in the first lesson:
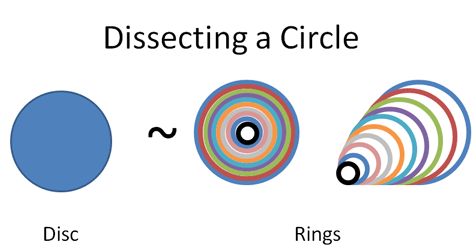
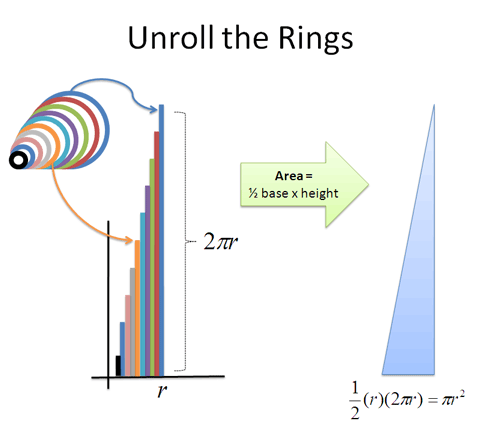
That’s what Calculus does: break a shape into pieces (the derivative), and glue it together in various ways (the integral). If you like this style of teaching, check out the full Calculus series.
A typical calculus syllabus covers integrals in week 12, after months of “building a foundation”. Better not use a complete sentence until we’ve studied adjectives, nouns and verbs separately, right? (My hand wringing could solve the energy crisis.)
The path to understanding isn’t always the most structured.
Happy math.
Update: This concept is called tacit knowledge, or “we know more than we can tell” (Michael Polanyi). Tacit knowledge is acquired through experience, and complements the explicit knowledge written as rules.
Other Posts In This Series
- Developing Your Intuition For Math
- Why Do We Learn Math?
- How to Develop a Mindset for Math
- Learning math? Think like a cartoonist.
- Math As Language: Understanding the Equals Sign
- Avoiding The Adjective Fallacy
- Finding Unity in the Math Wars
- Brevity Is Beautiful
- Learn Difficult Concepts with the ADEPT Method
- Intuition, Details and the Bow/Arrow Metaphor
- Learning To Learn: Intuition Isn't Optional
- Learning To Learn: Embrace Analogies
- Learning To Learn: Pencil, Then Ink
- Learning to Learn: Math Abstraction
- Learning Tip: Fix the Limiting Factor
- Honest and Realistic Guides for Learning
- Empathy-Driven Mathematics
- Studying a Course (Machine Learning) with the ADEPT Method
- Math and Analogies
- Colorized Math Equations
- Analogy: Math and Cooking
- Learning Math (Mega Man vs. Tetris)