Studying a Course (Machine Learning) with the ADEPT Method

What's the point of taking a class?

Build a lasting intuition for the key ideas.
During the course, understand it enough to solve problems.
After the course, enjoy it enough to revisit.

That's why I learn things. Non-goals are transcribing what a teacher says, or cramming only to forget everything. (Yeah, it's a game we play, but we're stepping off the treadmill and only cheating ourselves. Most subjects have useful insights buried somewhere.)

So, here's my strategy when studying:

If an idea clicks, write down the Aha! moment in language you'd use yourself.
If it doesn't, write down the Huh? moment. Move on and try again later (such as with the ADEPT method).

Keep it simple, like the KonMari method of organizing: Look at everything in your house. Does it spark joy? Keep what does, thank and donate what doesn't.

A simple study plan: Go through the material. Did it click? Write down what helped, otherwise look for a better explanation.

Actual Example: Stanford Machine Learning Course (Coursera)

My current learning project is the Machine Learning Class on Cousera. I've read a smattering of blog posts, the subject is growing, and after my friend asked me to join the class, I had to sign up. (It's great.)

Here's where I'm keeping my notes, Aha, and Huh moments:

Machine Learning Notes on Google Docs

This is one of the best learning experiences I can remember. A few examples:

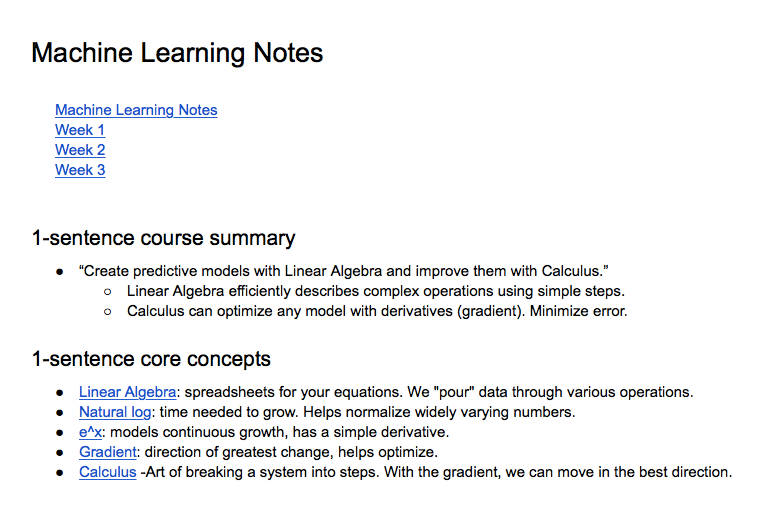
An Aha moment for each prerequisite

For the major concepts the course depends on, I keep a 5-second summary in mind. This underlying concept, why does it exist? In plain English, what does it mean?

Linear Algebra: spreadsheets for your equations. We "pour" data through various operations.
Natural log: time needed to grow. Helps normalize widely varying numbers.
e^x: models continuous growth, has a simple derivative.
Gradient: direction of greatest change, helps optimize.
Calculus -Art of breaking a system into steps. With the gradient, we can move in the best direction.

I reference these snippets as I encounter new formulas.

Huh moment: Need to clarify a Formula

There was a formula that I expected to be positive ("cost" should be positive), yet it had a negative sign out front. What gives?

It turns out I had forgotten a part of the derivation, where we expected the natural log to be negative. (This happens when we take the logarithm of numbers less than 1 — in other words, we are going "back in time" and shrinking.)

I would have preferred the equation written another way, and I made a note of this Huh? moment.

Huh moment: Why is it named that?

Early in the course, we define a "cost" function which tracks the difference between our predictions and the real value.

Why not call this difference something normal, like error?

It turns out "cost" is used because later in the course, we have items to minimize (like the number of variables in our model) which are not directly related to the error. The "cost" captures things outside the model, like the complexity we have. (If two models make equally accurate predictions, prefer the simpler one.)

Ah, "cost" can include fuzzier concepts. (I'd still prefer that laid out up-front.)

Aha moment: Summarize the Course in Plain English

As I go through the course, I have a plain-English definition in mind. What's it all about?

Machine Learning: Create models with Linear Algebra, then improve them with Calculus.

Linear Algebra lets us use many (tens, hundreds, thousands) of variables in a "math spreadsheet".
Calculus lets us improve our spreadsheet via feedback on how well it's working. Using functions like e^x, ln(x), x^2, etc. make it easy to take derivatives. Absolute value, if/then statements, etc. aren't easy to work with.

Now my thinking becomes: What types of predictive models can I make? If Linear Algebra can describe it, let's use it.

The Result: Notes You'll Actually Enjoy Reading

After the course is done, you're left with a set of notes that make sense to you: the Ahas, Huhs, and other gotchas. (This website is a running collection of mine.)

Future learning gets that much easier. Remember how you were confused about a topic a few years ago? Well, let's read the explanation you wrote to yourself on how to overcome it. Over time you build up a massive collection.

Other tips:

Embrace your confusion. The hesitation you feel when you see a formula is ok. Try to break down each part of the equation, ask what it means, make note of what is confusing and return over time. Every positive sign, every variable, why are they there?
It's ok to forget things - I do all the time. I just want a list of intuitions to load up when needed. Often a single phrase or diagram will bring it all back.
These notes are meant for you. Make them fast and quick. (My notes eventually become articles, but they stay informal and for my own use till then.)
The textbook already exists. Don't simply copy what the teacher/book said, add what you need to make it clear.

Show me your Aha! moments

This course is among the most fun I've had -- this is what learning should feel like, exploration with constant refinement. I'm curious to see if this approach helps you too.

For your next course, try keeping your notes in a single Google doc. Write down your Aha! and Huh? moments. Send me a link and I'll add them to this list:

Kalid Azad - Coursera Machine Learning
[you go here]

I'm curious to see what works for you, feedback is always welcome.

Happy math.