Years ago, while working on an explanation of the Fourier Transform, I found this diagram:
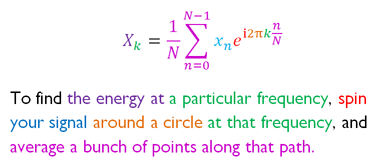
(source)
Argh! Why aren't more math concepts introduced this way?
Most ideas aren't inherently confusing, but their technical description can be (e.g., reading sheet music vs. hearing the song.)
My learning strategy is to find what actually helps when learning a concept, and do more of it. Not the stodgy description in the textbook -- what made it click for you?
The checklist of what I need is ADEPT: Analogy, Diagram, Example, Plain-English Definition, and Technical Definition.
Here's a few reasons I like the colorized equations so much:
- The plain-English description forces an analogy for the equation. Concepts like "energy", "path", "spin" aren't directly stated in the equation.
- The colors, text, and equations are themselves a diagram. Our eyes bounce back and forth, reading the equation like a map (not a string of symbols).
- The technical description -- our ultimate goal -- is not hidden. We're not choosing between intuition or technical, it's intuition for the technical.
Of course, we still need examples to check our understanding, but 4/5 ain't bad!
Creating Colorized Equations
I colorized a few of my favorite math topics below. Making the colorizations was surprisingly fun. Like writing a haiku, there's a game to trimming down a concept to its essence.
Colorized: e (universal base of growth)
.png)
The number e (2.718...) is the base of growth, generated from universal ideas. Take unit interest, with unit time and compound it perfectly. Read article.
Colorized: Euler's Formula

Euler's Formula is one of the most important in math, linking exponents, imaginary numbers, and circles. The intuition: constant growth in a perpendicular direction traces a circle. Read article.
Colorized: Fourier Transform
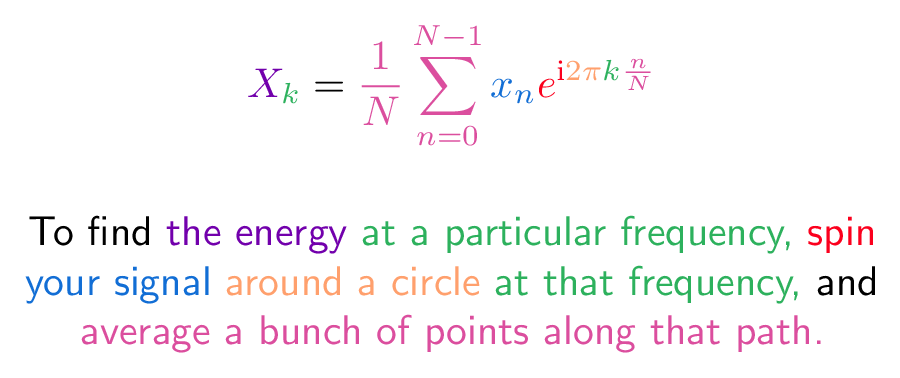
The Fourier Transform builds on Euler's Identity. Using your circular path, spin a signal at a certain speed to isolate the "recipe" at that speed (like separating a smoothie into its ingredients). Read article.
Colorized: Pythagorean Theorem

The Pythagorean Theorem is usually thought to apply to triangles only. In fact, it applies to any shape, any type of 2d area. Triangles are just a convenient starting point. Read article.
Colorized: Bayes Theorem

Bayes Theorem has a simple intuition: evidence must be diluted by false positives. (Cry wolf and you won't be trusted.) Read article.
Going Forward
These colorized equations are an experiment in conveying the most intuition in the simplest package possible. We don't need VR/AR, holograms, or brain-computer interfaces to understand math -- have we exhausted the possibilities of crayon on a piece of paper?
My short-term goal is create colorized equations for the top 25 equations on the site. Then (not trying to look directly at the sun), gather colorizations for the top (100?) topics we're meant to learn in high school and college.
The idea is to find explanation styles that work, and do more of them.
Happy math.
Appendix: How to Create Your Own
I have a half-built visual tool to make these. For now, here is the LaTeX template I used:
https://www.overleaf.com/read/cvmtqywqgvvw
Appendix: Initial Feedback
The idea got a strong reception on Twitter (thanks Jan):
colorized math equations makes it easier to understand. Great idea!! #ux #math https://t.co/8Btua0cpTl pic.twitter.com/2569UG2Zv4
— Jan Willem Tulp (@JanWillemTulp) December 14, 2017
The top piece of feedback was having accessible versions for color blind readers; I plan to make options available here too.
Other Posts In This Series
- Developing Your Intuition For Math
- Why Do We Learn Math?
- How to Develop a Mindset for Math
- Learning math? Think like a cartoonist.
- Math As Language: Understanding the Equals Sign
- Avoiding The Adjective Fallacy
- Finding Unity in the Math Wars
- Brevity Is Beautiful
- Learn Difficult Concepts with the ADEPT Method
- Intuition, Details and the Bow/Arrow Metaphor
- Learning To Learn: Intuition Isn't Optional
- Learning To Learn: Embrace Analogies
- Learning To Learn: Pencil, Then Ink
- Learning to Learn: Math Abstraction
- Learning Tip: Fix the Limiting Factor
- Honest and Realistic Guides for Learning
- Empathy-Driven Mathematics
- Studying a Course (Machine Learning) with the ADEPT Method
- Math and Analogies
- Colorized Math Equations
- Analogy: Math and Cooking
- Learning Math (Mega Man vs. Tetris)