What's a tough concept you finally figured out? (For me, it was the imaginary numbers. I'll never forget that Aha! moment.)
Ok. For that difficult concept, what finally made it click? It's usually:
- An analogy
- A diagram
- An example
- A friendly, plain-English description
Rarely is it because we're lacking:
- A technical definition
- A new technology
- A gamified incentive
- "more time" (I lack motivation, not time)
The limiting factor -- the thing holding me back -- is how I approach a concept.
The Roman Numeral Problem
Imagine you're teleported to a Roman classroom. Kids -- heck, the adults -- are struggling with multiplication. (IV times VII is really hard!)
What do you fix: Flip the classroom? Gamify things? Invent a printing press to distribute more worksheets?
Helpful, in time. But the first fix should be a simple discussion:
Hey, I'm from the future. Yes, it's pretty nice. But first, we need to fix your concept of a number. Individual lines for digits is cumbersome. Instead, think in groups of ones, tens, hundreds, and so on. Now multiplication is built into your numbers, and arithmetic gets a lot easier. Let me show you...
Boom. The "Roman Numeral Problem" is not fixed with better tech. Just a better understanding.
Ok. Imagine a time traveler (you, 6 months from now) is going to tutor you today. What would they suggest?
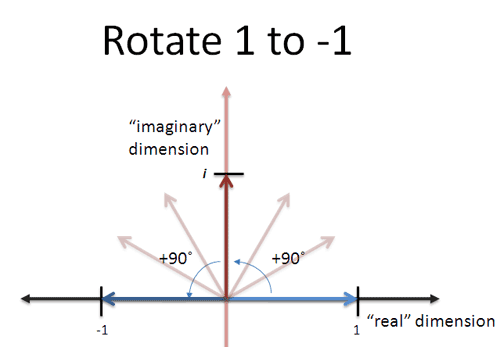
- Imaginary numbers: Don't try to conceptualize "the square root of a negative number". That's really clunky. Think about rotations instead.
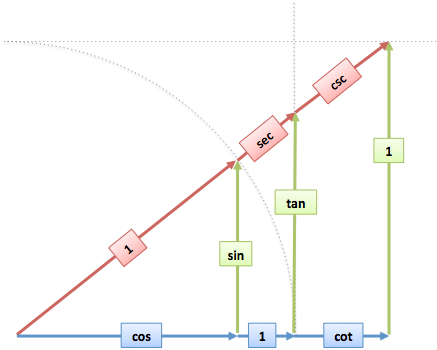
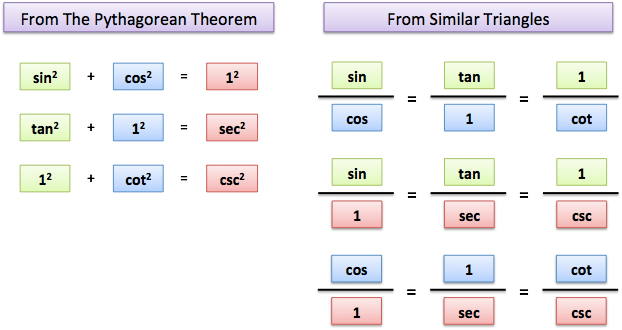
- Trigonometry: Don't try to memorize SOH-CAH-TOA and a mess of equations. Visualize a single diagram and the connections jump out.
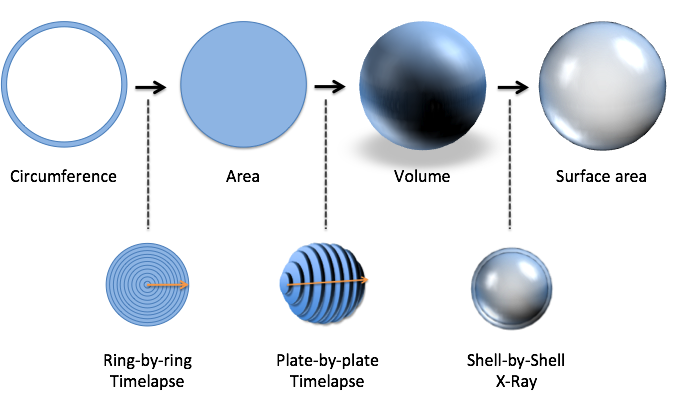
- Calculus: Don't force yourself through epsilon-delta proofs. Practice breaking things apart, putting them together, and get a feel for the patterns.
- Fourier Transform: Don't simply memorize the formula. Internalize the notion of a cycle recipe and practice going from a pattern, to the recipe, and back.
Focus on the problems a time traveler would fix first.
While drafting this post, a comment came in:
So, I just started learning about imaginary numbers in math class, and I was so confused. I understood the idea, but not the practical application or really what i was. I am a person who needs to understand a concept fully, I have trouble accepting that i=the square root of -1. I was googling it and I only got more confused. Then, I found your article on imaginary numbers, and all of a sudden, I got it. I could visualize it, even though I have no specific examples of their importance, I can understand why and how they could be important. It clicked. It doesn't make me want to go do my worksheet on adding and subtracting them, but in math tomorrow, I will be a much happier camper. -Abby
It drives me crazy to see endless tutorials on imaginary numbers that don't address the fundamental confusion of how a negative number can have a square root. You can give me all the videos and interactive quizzes you want, I'm not truly learning until you explain the notion of a rotation.
This misprioritization shows up everywhere:
Fix the plot, then worry about special effects.
Fix the recipe, then worry about decor.
Fix the melody, then worry about the instruments.
Fix the analogy, then worry about the presentation format.
Identify what's held you back and fix that first.
Happy math.
Appendix: Technology As The Education Fix
Technology helps with certain limitations (access, distribution, cost). But the quality of the source material is still up to us. I'd prefer handwritten letters with Socrates to a HD video conference with Carrot Top.
Veritasium has a great video on these lines ("This Will Revolutionize Education"):
If we think the limiting factor in education is still distribution, we'll focus on technical solutions.
But you know what? We've had Shakespeare online for a few decades now. Modern kids must be poetry experts because of free access to quality literature, right?
It's not an access problem any more. It's a motivation, interest, enthusiasm, understanding-what's-actually-going-on problem. Let's fix that first.
Other Posts In This Series
- Developing Your Intuition For Math
- Why Do We Learn Math?
- How to Develop a Mindset for Math
- Learning math? Think like a cartoonist.
- Math As Language: Understanding the Equals Sign
- Avoiding The Adjective Fallacy
- Finding Unity in the Math Wars
- Brevity Is Beautiful
- Learn Difficult Concepts with the ADEPT Method
- Intuition, Details and the Bow/Arrow Metaphor
- Learning To Learn: Intuition Isn't Optional
- Learning To Learn: Embrace Analogies
- Learning To Learn: Pencil, Then Ink
- Learning to Learn: Math Abstraction
- Learning Tip: Fix the Limiting Factor
- Honest and Realistic Guides for Learning
- Empathy-Driven Mathematics
- Studying a Course (Machine Learning) with the ADEPT Method
- Math and Analogies
- Colorized Math Equations
- Analogy: Math and Cooking
- Learning Math (Mega Man vs. Tetris)