Mega Man was one of my favorite video games. You're a little cyborg, running through levels and fighting end bosses:
Here's the trick: every boss has a weakness. After you beat Fire-man with your regular gun, you earn a fire weapon. This makes your upcoming fight with Ice-man easier, which helps defeat the next boss, and so on.


So why's this special?
In Mega Man, you look forward to fighting more bosses.
Every level is a chance to permanently upgrade your abilities, not a grind you're trying to survive.
The Tetris Mindset
Think about Tetris: would you look forward to a variety of new shapes appearing?
Heck no. Tetris can be fun in a "survive hordes of incoming zombies" sort of way, but in terms of learning, it's a frustrating, Sisyphean task. Every new piece is something to move beyond, not a learning opportunity. It's a test to find your breaking point.
In Mega Man, the game gets easier the more bosses you have. It's specifically designed for you to improve over time. Guess which game has 10+ sequels?
Conquering Euler's Formula
Math learning can follow the Mega Man pattern. If we want to beat "Dr. Euler", we need to beat his henchmen and master their weapons:
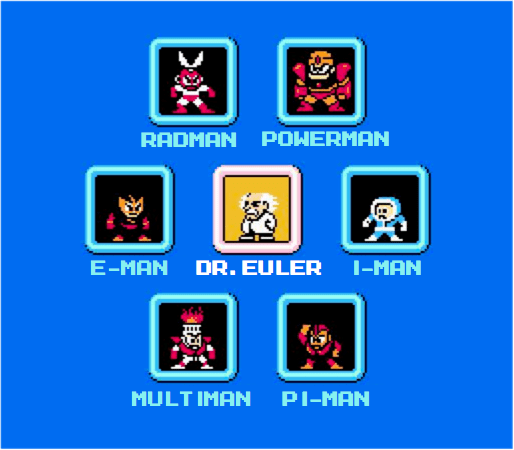
- Rad-man, once defeated, lets you think with radians, not just degrees
- Power-man lets you understand the base and power of an exponent
- I-man lets you unlock the rotation of imaginary numbers
- Pi-man lets you think in cyclic patterns
- Multi-man lets you understand how quantities transform each other
- E-man helps you visualize continuous change
- And finally, Dr. Euler lets you understand the role of imaginary exponents: $e^{ix} = \cos(x) + i\sin(x)$
After defeating the henchmen — truly understanding them and mimicking their abilities— Dr. Euler becomes defeatable. And after that, Boss Fourier. Then Captain Convolution.
There many more challenges on the horizon… and that's great! Every formula, once mastered, is a power to use.
When learning, I ask: "Did I internalize the concept so much I look forward to seeing it?". Learned ideas become allies, a decoder key to help unlock future equations.
The Mindset Shift
I constantly seek analogies for learning because my understanding has improved most from perspective shifts, not from studying specific concepts.
Despite years of math classes, I lacked intuitions on e, i, pi, radians, logs, exponents… (the list goes on). Math class involved grinding through Tetris levels, moving past the concepts and not absorbing them fully. Imaginary numbers were not friends I looked forward to seeing in an equation.
An Aha! moment helped me see learning as a set of additive skills we could internalize, and the process and challenges became something to look forward to. I hope the same shift happens for you. Wouldn't it be great to look forward to adding new abilities to your arsenal?
Happy math.
Other Posts In This Series
- Developing Your Intuition For Math
- Why Do We Learn Math?
- How to Develop a Mindset for Math
- Learning math? Think like a cartoonist.
- Math As Language: Understanding the Equals Sign
- Avoiding The Adjective Fallacy
- Finding Unity in the Math Wars
- Brevity Is Beautiful
- Learn Difficult Concepts with the ADEPT Method
- Intuition, Details and the Bow/Arrow Metaphor
- Learning To Learn: Intuition Isn't Optional
- Learning To Learn: Embrace Analogies
- Learning To Learn: Pencil, Then Ink
- Learning to Learn: Math Abstraction
- Learning Tip: Fix the Limiting Factor
- Honest and Realistic Guides for Learning
- Empathy-Driven Mathematics
- Studying a Course (Machine Learning) with the ADEPT Method
- Math and Analogies
- Colorized Math Equations
- Analogy: Math and Cooking
- Learning Math (Mega Man vs. Tetris)