Honest and Realistic Guides for Learning

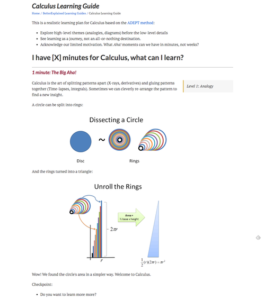
Summary: Check out the Calculus Learning Guide. I'm sharing an honest, realistic learning plan for what helped me enjoy the subject.

If you want a path that doesn't expect perfect motivation, shares insights in minutes (not weeks), and aims for lifelong insight, this guide is for you.

First Principles of Education

My learning strategy is to ask honest (sometimes uncomfortable) questions about what's really working.

No games, no kidding ourselves, just:

Did the concept I'm learning click?
If not, can I find a better explanation? (And let's share it.)

Here's my wishlist for a learning guide. Elon Musk talks about thinking from first principles, starting with fundamental truths and working forward from there¹. Who cares what's being done now, what's our goal?

Principle: Avoid teaching hatred of a subject

Priority #1 for any class is: Do not create hate for the subject.

Imagine 99% of people in a skiing class never ski again. They cringe at the thought. We wouldn't console ourselves thinking "Oh, skiing teaches important physical skills that apply to other fields." We'd think "That skiing class is awful and needs to change."

Sure, not everyone will love skiing (or cooking, or math), but they shouldn't detest it. Temporary understanding is not worth permanent aversion.

So, what Calculus introduction made me excited to learn more?

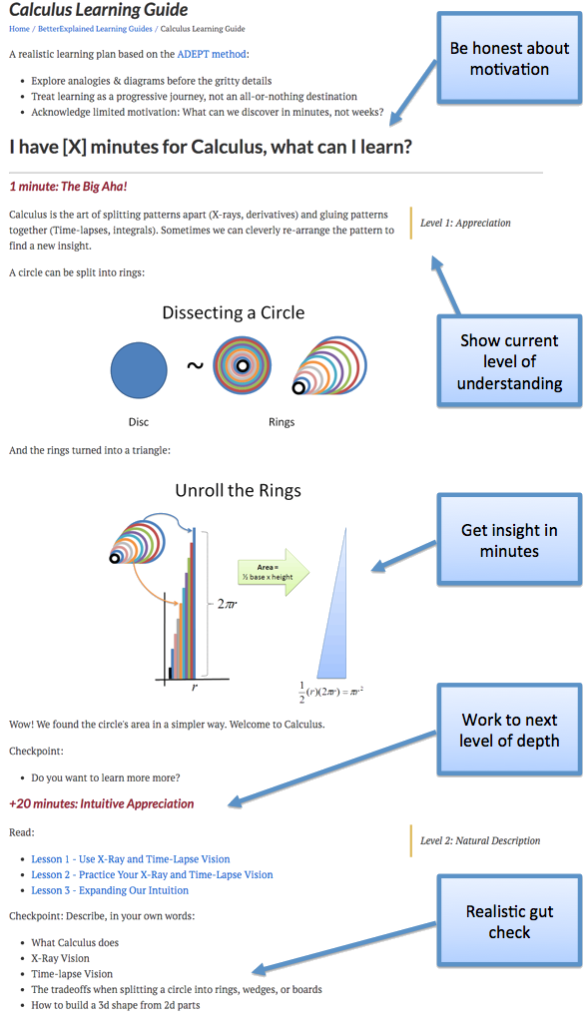
For me, it was seeing how patterns can be cleverly split and re-assembled:

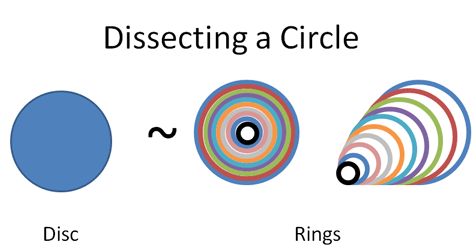
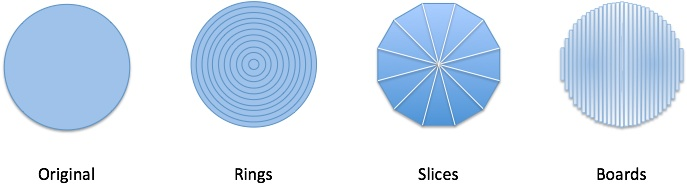
Most courses march you through weeks of theory "appreciate" these diagrams in week 11. Ugh. The big picture helps me appreciate the details, not the reverse.

Principle: Give Realistic Advice

A typical discussion:

"I want to learn Calculus. What should I do?"

"Here's a [full book/course/MOOC]. It's months of effort, I didn't do it myself, but here you go."

In other words, "go the library and read for 100 hours". The real question:

I'm interested in the subject. Is there a plan that worked for you?

Motivation is limited. Traditional classes "work" -- because students are under immense pressure to finish (tuition, peer pressure, fear of not graduating).

Online courses without this pressure have single-digit completion rates. We can pretend students "got something" from the experience, just like you "got something" from a movie you walked out of. We can't change the goalposts to "something is better than nothing" halfway through.

Realistic advice on what worked with my limited motivation (even as a math hobbyist!) is:

Get an Aha! moment in minutes that motivates me to keep going (a cool diagram, example, or simulation).
Take a progressive journey where even if I stop after an hour, I have some helpful insights (vs. an hour of stretching in the parking lot).
Maintain a desire to revisit the subject by having an approachable, gentle introduction. I'll then keep coming back to fill in gaps over time.

Principle: Don't Ignore Difficulties

For fun, find a lesson on imaginary numbers.

Does it acknowledge negative numbers were also distrusted?
Is the name "imaginary" described as an insult, given by people who didn't understand the concept?
Does the teacher mention their own confusion? (Or did imaginary numbers just click?)
Is there a real-world application? (If not, is this because it truly doesn't exist, we haven't tried to look, or it isn't important for learning?)

This type of lesson is a giant pet peeve. The flow is "Here's a confusing concept. I was confused myself, but I won't tell you that. Memorize the definition, apply it in these practice problems, and we'll call it a day."

Argh, this drives me nuts. It reinforces the stereotype that math class is a game of moving symbols around. (This symbol multiplied by this other symbol makes -1. Tada!)

It's ok to lack an intuition; I lack it for most things. But hiding our initial confusion implies the subject isn't confusing.

Principle: Expect to get it wrong sometimes

There's a common trope of the smart-aleck student trying to "outsmart" the teacher. Do basketball players try to "outsmart" their coach?

The flawed assumption is teachers must be some omniscient authority giving you access to precious knowledge. The knowledge is out there, it's not like the teacher invented the math herself. Instead, imagine a coach who is trying to improve your understanding.

Coaches can be wrong, sure. But they've seen many struggle with the same issues you're facing, and are trying to help. It's ok if Lebron James can dunk better than his coach.

The math may be perfect and unchanging, but the way it's taught is not. Let's make it easy to improve lessons and not expect perfection the first time.

Principle: We have Different Goals

Most courses assume you want mastery of the subject. That's fine, but is it necessary?

There are several levels of music understanding:

Intuitive Appreciation: Just enjoying the music.
Natural Description: Humming a tune you heard or made up.
Symbolic Description: Reading and writing the sheet music.
Theory: Explaining how harmonies work, why minor scales are somber, etc.
Performance: Playing the official instruments.

In language learning, there is an ILR scale from no profiency to native fluency. Not everyone studying Calculus needs to become Isaac Newton. Can we have a path that goes as far as we need?

An Honest and Realistic Learning Plan

Combining these insights, I've made a Calculus Learning Guide.

The principles, as I tried to apply them:

It's honest. It's the explanation that actually inspired me, not the theoretical explanation that requires weeks of discipline for some future payoff.
It acknowledges limited motivation. How far can you get in 1 minute? 10 minutes? An hour? Pretty far, I think. And getting a win in 10 minutes means you'll come back for more.
It's updatable. With lessons based primarily on text, we can easily update, re-arrange, add, edit, fix. Other formats are essentially a bet we got it right the first time.
It acknowledges levels of understanding. Most people just want an appreciation for Calculus. Technical performance is a goal we can separate, organize, and build a path to.
I eat the veggies myself. This guide has "gut checks" like "Can I describe an integral in everyday terms?" and "Can I derive the product rule on my own?". This is how I actually refresh my Calculus understanding.

In my ideal world, every Wikipedia topic would have a guide that took you from the 1-minute version to a full technical understanding. Go as far as you wish, make meaningful progress at each step, and have fun along the way.

Happy math.

Musk mentions not "reasoning by analogy", or assuming a conclusion is true based on what happened in another scenairo. This is different from "understand by analogy", getting the gist of an idea and then working to the technical version. The analogy is a raft to cross the river, to be left behind once you're on land. ↩