The Pythagorean Theorem is often taken as a fact about right triangles.
Let's try a broader interpretation: The Pythagorean Theorem explains how 2D area can be combined.
Here's what I mean. Suppose we have two lines lying around (the creatively named Line A and Line B). We can spin them to create area:
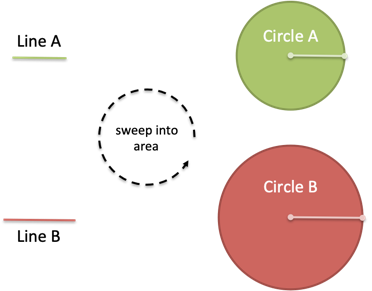
Ok, fun enough. Where's the mystery?
Well, what happens if we combine the line segments before spinning them?
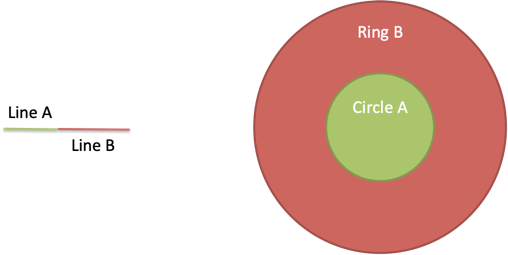
Whoa. The area swept out seems to change. Should simply moving the lines, not lengthening them, change the area?
Running The Numbers
Eyeballing the diagram above, it sure seems like the area grew. Let's work out the specifics.
As an example, suppose $a = 6$ and $b = 8$. When they're swept into circles ($\text{area} = \pi r^2$) we get:
![]()
![]()
For a total of $36\pi + 64\pi = 100\pi$.
The combined segment has length $c = a + b = 14$, and when we spin it we get:
![]()
Uh oh. That's way more area than before.
The Problem
What happened? Well, Circle A didn't change. But Circle B is much less than Ring B (just look at it!).
The issue: When Line B spins on its own, it can only reach 8 units out as it sweeps. When we attach Line B to Line A, it reaches out 6 + 8 = 14 units. Now the circular sweep covers more area, meaning Circle B is smaller than Ring B.
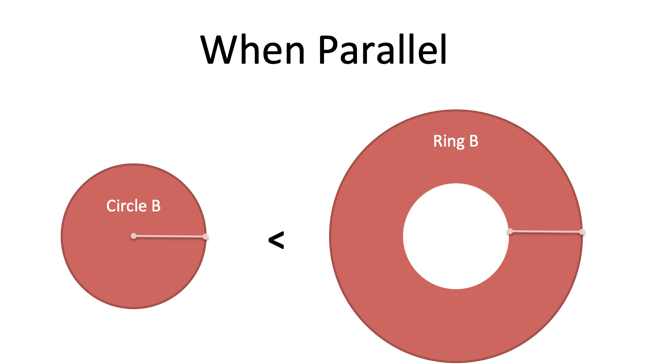
Mathematically, here's what happened.
![]()
Ignore $\pi$ for a moment since it's a common term. When expanding $c^2 = (a + b)^2 = a^2 + 2ab + b^2$, there's a new $2ab$ term that has to go somewhere. Because Circle A doesn't change, this extra area must appear in Ring B.
Making Things Line Up
It... sort of makes sense that the area changes, but I don't like it. Just moving things around shouldn't have this effect! Can the area ever be the same?
Sure, if we remove the $2ab$ term. The easy fix is to set $a=0$, but that's cheating and you know it.
Let's find a clever solution. Intuitively, the question is: How can Line A's length not help Line B as it spins?
Tilt it! As we rotate Line B, there's less benefit from Line A's length. Ladders are useless when lying on the floor, right?
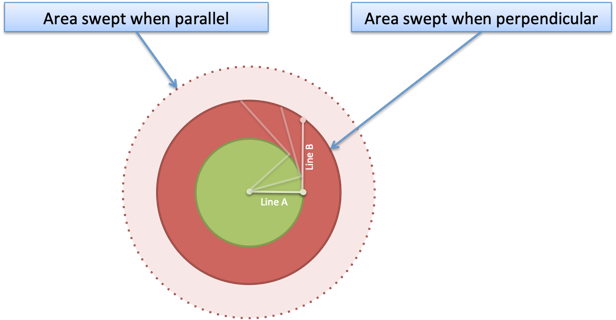
When we go Full Perpendicular™, the $2ab$ term disappears and Circle B = Ring B. (In vector terms, the dot product is zero: $a \cdot b = 0$).
Ah -- that's the meaning of the Pythagorean Theorem. When line segments are perpendicular, the same area is swept whether the lines are combined or separated.
Checking The Math
It's not a bad idea to make sure the numbers line up.
Since the segments are now perpendicular, we know $c^2 = a^2 + b^2$, so:
![]()
![]()
Now we can calculate:
![]()
Tada! The Ring and Circle sweep the same area.
In our example, we have Circle A = $36\pi$, Circle B = $64 \pi$, $c = \sqrt{36 + 64} = 10$. The ring width is $10 - 6 = 4$.
Summary
The Pythagorean Theorem is about more than triangles. When components are perpendicular, the area they make is independent of how they are arranged.

Appendix: Assorted Thoughts
- The Law of Cosines explicitly shows the $2ab$ term which assumed to be zero in the Pythagorean Theorem. The area of Ring B can even be "negative" if we tilt Line B to point inside.
- We can combine area from multiple dimensions ($x^2 + y^2 + z^2 + ...$). As long as they are mutually perpendicular, the area swept by each dimension is the area swept by the total.
- The Pythagorean Theorem is a relationship in the 2D area domain ($c^2 = a^2 + b^2$). We start here and convert this to a relationship in the 1D domain ($c = \sqrt{a^2 + b^2}$). The conversion happens so often we forget where it began.
- More on sweeping area: https://www.cut-the-knot.org/Curriculum/Geometry/PythFromRing.shtml
Happy math.
