The Pythagorean Theorem shows how strange our concept of distance is. Using the rule $a^2 + b^2 = c^2$, we can trade some "a" to get more "b".
Starting with
![]()
means "A 13-inch pizza equals a 13-inch pizza". Sure. But we can trade an inch and get:
![]()
Huh? A 12-inch pizza and a 5-inch pizza equal a 13-inch pizza?
The math works (144 + 25 = 169) but, but... we gave up an inch and got a five-inch pizza!
Let's understand why the tradeoff happens, and how to use it.
Explanation 1: Shaving the Square
A key insight: Bigger numbers are harder to square.
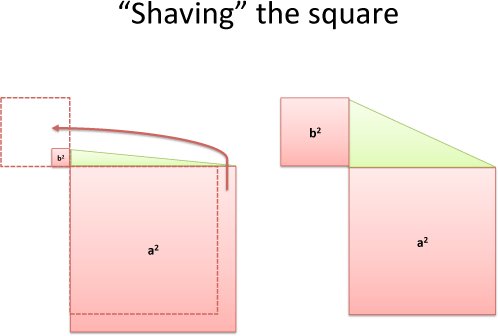
Imagine laying tiles on a porch -- as your porch grows, the outer layer needs more tiles. Trimming a 13x13 porch to 12x12 frees up 25 tiles, which is enough to make a new 5x5 porch!
I call this "shaving the square". Trimming 1 unit from the outside of a large square has more "shavings" which can contribute to a smaller one (trimming an inch from a giant fro can make a sweater for an infant). As we continue to trim, the benefit diminishes because our starting point is smaller and smaller.
Explanation 2: Sliding the Chopstick
A second insight: Slide a little, pivot a lot.
Imagine a chopstick wedged in a corner: the length is fixed, and the ends of the chopstick must touch a wall. What're the options?
Well, laying on a single wall means 100% for one side (like saying $13^2 + 0^2 = 13^2$). Not that interesting.
By sliding the chopstick (from 13 to 12) we can swing it out by 5 on the other wall!
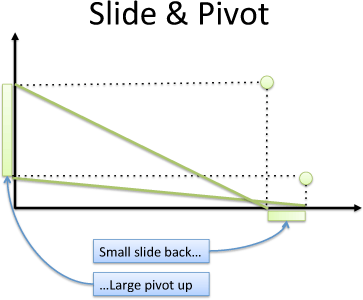
You need to try it -- a small slide gives a giant pivot. As we keep sliding, the tradeoff (How much pivot do we get?) changes.
So What's the Tradeoff?
Time to see how the a/b tradeoff works. First, let's use grid coordinates: x & y (horizontal and vertical). Given a fixed distance (13 units, let's say), our options lay on the circle where $x^2 + y^2 = 13^2$:
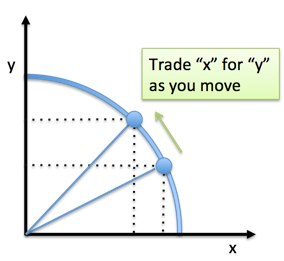
A few points:
- Each possibility is the same distance, but has a different ratio of x to y (100% x, 100% y, or a mix like (12,5))
- We can only move to neighboring points on the circle (options at the same distance)
- The tradeoff we face is how much "x" we get for "y" when moving to a neighbor. If we're at (0, 13) we could move to (5, 12). This trades 1 y for 5 x's.
This is the "chunky" tradeoff where we're using an entire unit at a time. What about .5 units? .01?
Enter the tangent! The tangent line shows the trajectory of our current path, the direction to our neighbor. We follow the tangent for a tiny, microscopic amount to get our next neighbor. The tangent is an approximation -- it's not pointing exactly at our nearest neighbor, but it's pretty close.
The tangent shows the tradeoff you are about to make.
What's the actual amount? Any point (x,y) has a slope of y/x, and a tangent line with slope -x/y, so the tradeoff is...getting confused yet?
Less mindless algebra, more intuition:
- Circles have a tangent line perpendicular to the current point
- If you're at (5,12) then tangent slope is some ratio of 5 and 12
- Remember "shaving the square": you get a better deal in the direction of the smaller coordinate (increasing a large square is tough).
- So, at (5, 12) you're "heavy on the y" and the trade will favor improving your x: it should be "trade 5 y's for 12 x's". And why not the other way? It doesn't make sense that the more y you have, the easier it is to get y! That'd spiral off into exponential growth, not a circle.
- Lastly, we can't trade an entire chunk of 5 y's! The tangent is about our nearest neighbor. We have a trade of 12/5 or 2.4 to 1. Our next, tiny movement will be at this ratio (and then we'll be at a new point, with a new tangent).
General principle: Our neighbors are on a circle, which encourages balance. You get a better deal in the direction of the smaller coordinate: at (x,y) the tradeoff is y:x.
Optimizing The Tradeoff
Now we know the tradeoff for any point (x,y) -- let's optimize!
In a boring scenario, we get paid based on pure distance, so every point (or direction to move) is the same.
The exciting scenario: our (x,y) position is an input into some other function which gives us a return! Now we want to maximize that function.
Here's a scenario: Popeye throws cars for cash. He lines up spectators on fences running North and East. The spectators must look straight ahead (they're in neck braces, due to earlier events) but will pay Popeye if they see a car pass in front of them.
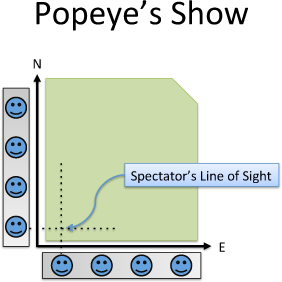
Maximizing Even Payouts
Suppose each spectator offers \$1 if they see the car (Payout (x,y) = x + y). Where to throw?
First, assume Popeye has finite energy -- he can throw the car 13 meters. Now let's start somewhere: throwing the car pure North (0, 13):
![]()
Ok. What if he threw it slightly East? To (5, 12) let's say?
![]()
Clearly better. This should make sense: at (0,13) the tradeoff is great to get more East. We can give up 1 North and get a whopping 5 East, a "profit" of \$4 if we do the trade. We should keep trading as long as it's profitable -- as long as we're out of balance, the circle will reward us for boosting the smaller side. Following a 45 degree angle for 13 units is the ideal:
![]()
Neat. A 45-degree throw hits 70.7% of the possible spectators for each side.
Psst. Confused about how a 45-degree through passes by 70.7% of the spectators on each side? No problem.
A 45-degree throw is along the diagonal of a square. A triangle with sides 1 and 1 has a hypotenuse of:
![]()
And has sides $(1, 1, 1.414)$.
A hypotenuse of $\sqrt{2}$ isn't convenient: it's hard to know what fraction a side is of the whole. We divide the triangle by the length of the hypotenuse ($\sqrt{2}$), making the hypotenuse 1 and the other sides a percentage:
![]()
Now we've discovered that a 45-degree throw, with sides $(1, 1, \sqrt{2})$, has the ratio $.707, .707, 1$. 70.7% of the distance along the hypotenuse shows up on each side.
General Technique: Finding the Best Direction
We stumbled upon the way to find the best return:
- Pick any starting point / direction
- Tweak it: if our return improves, keep the new choice (it's profitable)
- Keep tweaking until our return is no longer profitable
In math slang, this is "finding the local maximum". In economics slang, it's finding the point of "zero marginal returns". Popeye calls it Squeezing the Spinach.
Maximizing Uneven Returns
Now suppose the Northern spectators offer \$2 (Eastern stay at \$1), so P(x,y) = x + 2*y. Should we throw it 100% North?
![]()
Not bad. But what about 45 degrees again?
![]()
Interesting -- 45 degrees is still better! But... I think we went too far! Shouldn't we favor North since it pays more?
Yep. Let's remember how to Squeeze the Spinach (maximize our returns): start with North and change until it's not profitable:
- The payout function means 1 North = 2 Easts (North pays \$2, so 1 unit North = 2 units East)
- Trades are profitable if we can beat 1 North for 2 Easts (1 North for 3 Easts, for example, would profit \$1)
So... where are trades better than 1 North for 2 Easts? In the Northern section, where the circle rewards us by throwing Easts at us ("Please, please go East... I'll give you a bunch if you give up a little North").
Remember how circles are about x/y, x & y, x:y, etc.? Well, we have the numbers 1 and 2. (2,1) is in the East section. We want (1,2). Why? At (1,2) we have reached the perfect 1 North = 2 East tradeoff.
Following the direction (1,2) for 13 units is:
![]()
Tada! Over 29 smackeroos because we maximized our return.
The Gradient Principle
We can supercharge this result:
To maximize return, go in each direction proportional to its payoff.
If North pays 2:1 compared to East, your trajectory should favor North by 2:1. In mathier terms:
- Payoff(x,y) = ax + by
- Best trajectory = (a, b) [in our case, (East, North) => (1, 2)]
And this works in multiple dimensions! Given 3 dimensions, go in a direction (Payoff(x), Payoff(y), Payoff(z)). Vector calculus fans, this is why the gradient is in the direction of greatest increase.
The gradient for $F(x,y,z)$ is
![]()
And each partial derivative (dF/dx) is the payoff for moving in that direction.
But does it all balance? Suppose x pays 3, y pays 4, and z pays 5 (at the current position). The 2-dimensional tradeoff trajectories are:
![]()
![]()
![]()
Now for the magic: the combined trajectory
![]()
satisfies all 3 requirements! On the x-z plane, x doesn't care about y -- as long as the ratio to z is (3 , ?, 5) you're getting the best tradeoff from the x-z perspective. The pairs are:
- (3, ?, 5)
- (?, 4, 5)
- (3, 4, ?)
You don't need a sudoku master to see (3, 4, 5) satisfies all those proportions.
Still not convinced? Imagine the payoff for y was zero. We don't want to waste energy in our trajectory (3, ?, 5) in a useless direction. But that can't happen, because the y-z tradeoff will be (?, 0, 5) and the x-y tradeoff will be (3, 0, ?). The x-z tradeoff lets y-z and x-y "figure out" what y should be, which is 0.
Questions I Had That You Might Have Too
Q: I still don't get why this works at all. Somehow 50% in x and 50% in y leads to .7 + .7 = 1.4?
It's a deep question about why space behaves like this. I was going crazy staring at chopsticks on a wall.
Here's my answer: distance is distance. 13 units is 13 units. But in some situations we are "measuring our coordinates" (what are the values of x & y) and not the distance itself.
Cartesian coordinates (x-axis, y-axis) are very inefficient for diagonal motion (i.e., you are measuring the sides of the triangle, not the hypotenuse). When $.707^2 + .707^2 = 1$, it's a measure how how "inefficient" our x & y coordinates are being. We used 70% of each coordinate to represent an object that could have been 100% on one (i.e, if we used polar coordinates).
Q: I have an offshore investment with 200% return, and an onshore one with 5% return. I have \$1000 to spend -- should I split my money?
Heavens, no! Remember, this principle is about distance measurements on a grid with the idea that 50% in x and 50% in y covers "more ground" than 100% in x. In investing 1) money is not on a grid and 2) there's no distance bonus. Putting half your money in each is plain old 0.5 + 0.5 = 1.0. Giving up \$1 of the offshore investment gives you \$1 for the onshore one.
Put all your money in the best investment.
Q: So all this stuff is useless?
Heavens, no! Ask yourself: am I measuring distance on a coordinate system?
Many things are measured in terms of x-y coordinates (physical phenomena, etc.) and do have the Pythagorean distance tradeoff.
But not every graph is the same. Graphs that aren't about distance (like "Money vs. Time") do not get any boost from the Pythagorean theorem. This confused me for a long time: the Pythagorean Theorem works for coordinate distance!
Final Thoughts
The Pythagorean Theorem is so versatile -- it's not about triangles, it covers the nature of distance. I seem to find some new realization when I study it. Really grokking it will help you everywhere, from geometry to vector calculus.
Happy math.
Other Posts In This Series
- Vector Calculus: Understanding the Dot Product
- Vector Calculus: Understanding the Cross Product
- Vector Calculus: Understanding Flux
- Vector Calculus: Understanding Divergence
- Vector Calculus: Understanding Circulation and Curl
- Vector Calculus: Understanding the Gradient
- Understanding Pythagorean Distance and the Gradient
