How To Understand Derivatives: The Quotient Rule, Exponents, and Logarithms

Last time we tackled derivatives with a "machine" metaphor. Functions are a machine with an input (x) and output (y) lever. The derivative, dy/dx, is how much "output wiggle" we get when we wiggle the input:

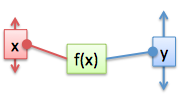
Now, we can make a bigger machine from smaller ones (h = f + g, h = f * g, etc.). The derivative rules (addition rule, product rule) give us the "overall wiggle" in terms of the parts. The chain rule is special: we can "zoom into" a single derivative and rewrite it in terms of another input (like converting "miles per hour" to "miles per minute" -- we're converting the "time" input).

And with that recap, let's build our intuition for the advanced derivative rules. Onward!

Division (Quotient Rule)

Ah, the quotient rule -- the one nobody remembers. Oh, maybe you memorized it with a song like "Low dee high, high dee low...", but that's not understanding!

It's time to visualize the division rule (who says "quotient" in real life?). The key is to see division as a type of multiplication:

$\displaystyle{h = \frac{f}{g} = f \cdot \frac{1}{g}}$

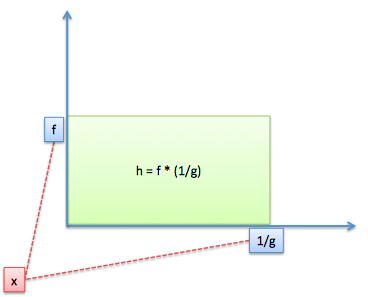
We have a rectangle, we have area, but the sides are "f" and "1/g". Input x changes off on the side (by dx), so f and g change (by df and dg)... but how does 1/g behave?

Chain rule to the rescue! We can wrap up 1/g into a nice, clean variable and then "zoom in" to see that yes, it has a division inside.

So let's pretend 1/g is a separate function, m. Inside function m is a division, but ignore that for a minute. We just want to combine two perspectives:

f changes by df, contributing area df * m = df * (1 / g)
m changes by dm, contributing area dm * f = ?

We turned m into 1/g easily. Fine. But what is dm (how much 1/g changed) in terms of dg (how much g changed)?

We want the difference between neighboring values of 1/g: 1/g and 1/(g + dg). For example:

What's the difference between 1/4 and 1/3? 1/12
How about 1/5 and 1/4? 1/20
How about 1/6 and 1/5? 1/30

How does this work? We get the common denominator: for 1/3 and 1/4, it's 1/12. And the difference between "neighbors" (like 1/3 and 1/4) will be 1 / common denominator, aka 1 / (x * (x + 1)). See if you can work out why!

$\displaystyle{\frac{1}{x + 1} - \frac{1}{x} = \frac{-1}{x(x+1)}}$

If we make our derivative model perfect, and assume there's no difference between neighbors, the +1 goes away and we get:

$\displaystyle{\frac{-1}{x(x+1)} \sim \frac{-1}{x^2}}$

(This is useful as a general fact: The change from 1/100 to 1/101 = one ten thousandth)

The difference is negative, because the new value (1/4) is smaller than the original (1/3). So what's the actual change?

g changes by dg, so 1/g becomes 1/(g + dg)
The instant rate of change is -1/g^2 [as we saw earlier]
The total change = dg * rate, or dg * (-1/g^2)

A few gut checks:

Why is the derivative negative? As dg increases, the denominator gets larger, the total value gets smaller, so we're actually shrinking (1/3 to 1/4 is a shrink of 1/12).
Why do we have -1/g^2 * dg and not just -1/g^2? (This confused me at first). Remember, -1/g^2 is the chain rule conversion factor between the "g" and "1/g" scales (like saying 1 hour = 60 minutes). Fine. You still need to multiply by how far you went on the "g" scale, aka dg! An hour may be 60 minutes, but how many do you want to convert?
Where does dm fit in? m is another name for 1/g. dm represents the total change in 1/g, which as we saw, was -1/g^2 * dg. This substitution trick is used all over calculus to help split up gnarly calculations. "Oh, it looks like we're doing a straight multiplication. Whoops, we zoomed in and saw one variable is actually a division -- change perspective to the inner variable, and multiply by the conversion factor".

Phew. To convert our "dg" wiggle into a "dm" wiggle we do:

$\displaystyle{dm = \frac{-1}{g^2} \cdot dg}$

And get:

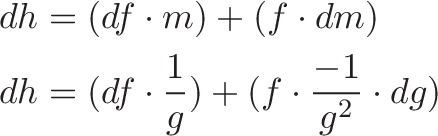
$\begin{aligned} dh &= (df \cdot m) + (f \cdot dm) \\ dh &= (df \cdot \frac{1}{g}) + (f \cdot \frac{-1}{g^2} \cdot dg) \end{aligned}$

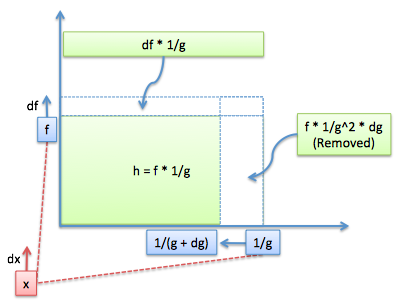
Yay! Now, your overeager textbook may simplify this to:

$\displaystyle{ dh = \frac{df \cdot g - f \cdot dg}{g^2}}$

and it burns! It burns! This "simplification" hides how the division rule is just a variation of the product rule. Remember, there's still two slivers of area to combine:

The "f" (numerator) sliver grows as expected
The "g" (denominator) sliver is negative (as g increases, the area gets smaller)

Using your intuition, you know it's the denominator that's contributing the negative change.

Exponents (e^x)

e is my favorite number. It has the property

$\displaystyle{\frac{d}{dx} e^x = e^x}$

which means, in English, "e changes by 100% of its current amount" (read more).

The "current amount" assumes x is the exponent, and we want changes from x's point of view (df/dx). What if u(x)=x^2 is the exponent, but we still want changes from x's point of view?

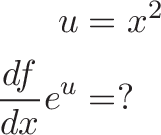
$\begin{aligned} u &= x^2 \\ \frac{df}{dx} e^u &= ? \end{aligned}$

It's the chain rule again -- we want to zoom into u, get to x, and see how a wiggle of dx changes the whole system:

x changes by dx
u changes by du/dx, or d(x^2)/dx = 2x
How does e^u change?

Now remember, e^u doesn't know we want changes from x's point of view. e only knows its derivative is 100% of the current amount, which is the exponent u:

$\displaystyle{ \frac{d(e^u)}{du} = e^u }$

The overall change, on a per-x basis is:

$\displaystyle{ \frac{d(e^u)}{dx} = \frac{du}{dx} e^u = 2x \cdot e^u = 2x \cdot e^{x^2} }$

This confused me at first. I originally thought the derivative would require us to bring down "u". No -- the derivative of e^foo is e^foo. No more.

But if foo is controlled by anything else, then we need to multiply the rate of change by the conversion factor (d(foo)/dx) when we jump into that inner point of view.

Natural Logarithm

The derivative is ln(x) is 1/x. It's usually given as a matter-of-fact.

My intuition is to see ln(x) as the time needed to grow to x:

ln(10) is the time to grow from 1 to 10, assuming 100% continuous growth

Ok, fine. How long does it take to grow to the "next" value, like 11? (x + dx, where dx = 1)

When we're at x=10, we're growing exponentially at 10 units per second. It takes roughly 1/10 of a second (1/x) to get to the next value. And when we're at x=11, it takes 1/11 of a second to get to 12. And so on: the time to the next value is 1/x.

The derivative

$\displaystyle{\frac{d}{dx}\ln(x) = \frac{1}{x}}$

is mainly a fact to memorize, but it makes sense with a "time to grow" intepreration.

A Hairy Example: x^x

Time to test our intuition: what's the derivative of x^x?

$\displaystyle{\frac{d}{dx} x^x = ? }$

This is a bad mamma jamma. There's two approaches:

Approach 1: Rewrite everything in terms of e.

Oh e, you're so marvelous:

$\begin{aligned} h(x) &= x^x \\ &= [e^{\ln(x)}]^x \\ &= e^{\ln(x) \cdot x} \end{aligned}$

Any exponent (a^b) is really just e in different clothing: [e^ln(a)]^b. We're just asking for the derivative of e^foo, where foo = ln(x) * x.

But wait! Since we want the derivative in terms of "x", not foo, we need to jump into x's point of view and multiply by d(foo)/dx:

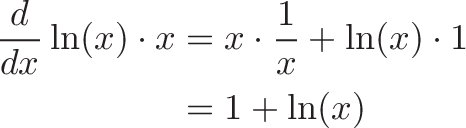
$\begin{aligned} \frac{d}{dx} \ln(x) \cdot x &= x \cdot \frac{1}{x} + \ln(x) \cdot 1 \\ &= 1 + \ln(x) \end{aligned}$

The derivative of "ln(x) * x" is just a quick application of the product rule. If h=x^x, the final result is:

$\displaystyle{h'(x) = (1 + \ln(x)) \cdot e^{\ln(x) \cdot x} = (1 + \ln(x)) \cdot x^x}$

We wrote e^[ln(x)*x] in its original notation, x^x. Yay! The intuition was "rewrite in terms of e and follow the chain rule".

Approach 2: Independent Points Of View

Remember, deriviatives assume each part of the system works independently. Rather than seeing x^x as a giant glob, assume it's made from two interacting functions: u^v. We can then add their individual contributions. We're sneaky though, u and v are the same (u = v = x), but don't let them know!

From u's point of view, v is just a static power (i.e., if v=3, then it's u^3) so we have:

$\displaystyle{\frac{d}{du} u^v = v \cdot u^{v - 1}}$

And from v's point of view, u is just some static base (if u=5, we have 5^v). We rewrite into base e, and we get

$\begin{aligned} \frac{d}{dv} u^v &= \frac{d}{dv} [e^{\ln(u)}]^v \\ &= \frac{d}{dv} e^{\ln(u) \cdot v} \\ &= \ln(u) \cdot e^{\ln(u) \cdot v} \end{aligned}$

We add each point of view for the total change:

$\displaystyle{\ln(u) \cdot e^{\ln(u) \cdot v} + v \cdot u^{v - 1} }$

And the reveal: u = v = x! There's no conversion factor for this new viewpoint (du/dx = dv/dx = dx/dx = 1), and we have:

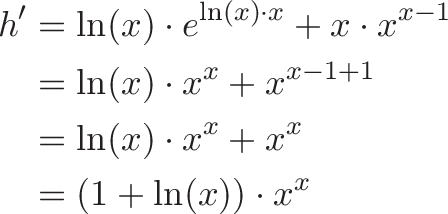
$\begin{aligned} h' &= \ln(x) \cdot e^{\ln(x) \cdot x} + x \cdot x^{x - 1} \\ &= \ln(x) \cdot x^x + x^{x - 1 + 1} \\ &= \ln(x) \cdot x^x + x^x \\ &= (1 + \ln(x)) \cdot x^x \end{aligned}$

It's the same as before! I was pretty excited to approach x^x from a few different angles.

By the way, use Wolfram Alpha (like so) to check your work on derivatives (click "show steps").

Question: If u were more complex, where would we use du/dx?

Imagine u was a more complex function like u=x^2 + 3: where would we multiply by du/dx?

Let's think about it: du/dx only comes into play from u's point of view (when v is changing, u is a static value, and it doesn't matter that u can be further broken down in terms of x). u's contribution is

$\displaystyle{\frac{d}{du} u^v = v \cdot u^{v - 1}}$

if we wanted the "dx" point of view, we'd include du/dx here:

$\displaystyle{\frac{d}{du} \frac{du}{dx} u^v = v \cdot u^{v - 1} \frac{du}{dx}}$

We're multiplying by the "du/dx" conversion factor to get things from x's point of view. Similarly, if v were more complex, we'd have a dv/dx term when computing v's point of view.

Look what happened -- we figured out the genric d/du and converted it into a more specific d/dx when needed.

It's Easier With Infinitesimals

Separating dy from dx in dy/dx is "against the rules" of limits, but works great with infinitesimals. You can figure out the derivative rules really quickly:

Product rule:

$\begin{aligned} (fg)' &= (f + df)(g + dg) - fg \\ &= [fg + f dg + g df + df dg ]- fg \\ &= f dg + g df + df dg \end{aligned}$

We set "df * dg" to zero when jumping out of the infinitesimal world and back to our regular number system.

Think in terms of "How much did g change? How much did f change?" and derivatives snap into place much easier. "Divide through" by dx at the end.

Summary: See the Machine

Our goal is to understand calculus intuition, not memorization. I need a few analogies to get me thinking:

Functions are machines, derivatives are the "wiggle" behavior
Derivative rules find the "overall wiggle" in terms of the wiggles of each part
The chain rule zooms into a perspective (hours => minutes)
The product rule adds area
The quotient rule adds area (but one area contribution is negative)
e changes by 100% of the current amount (d/dx e^x = 100% * e^x)
natural log is the time for e^x to reach the next value (x units/sec means 1/x to the next value)

With practice, ideas start clicking. Don't worry about getting tripped up -- I still tried to overuse the chain-rule when working with exponents. Learning is a process!

Happy math.

Appendix: Partial Derivatives

Let's say our function depends on two inputs:

$\displaystyle{f(x,y)}$

The derivative of f can be seen from x's point of view (how does f change with x?) or y's point of view (how does f change with y?). It's the same idea: we have two "independent" perspectives that we combine for the overall behavior (it's like combining the point of view of two Solipsists, who think they're the only "real" people in the universe).

If x and y depend on the same variable (like t, time), we can write the following:

$\displaystyle{\frac{df}{dt} = \frac{df}{dx} \cdot \frac{dx}{dt} + \frac{df}{dy} \cdot \frac{dy}{dt}}$

It's a bit of the chain rule -- we're combining two perspectives, and for each perspective, we dive into its root cause (time).

If x and y are otherwise independent, we represent the derivative along each axis in a vector:

$\displaystyle{(\frac{df}{dx}, \frac{df}{dy})}$

This is the gradient, a way to represent "From this point, if you travel in the x or y direction, here's how you'll change". We combined our 1-dimensional "points of view" to get an understanding of the entire 2d system. Whoa.