I usually avoid current events, but recent skirmishes in the math world prompted me to chime in. To recap, there’ve been heated discussions about math education and the role of online resources like Khan Academy.
As fun as a good math showdown may appear, there’s a bigger threat: Apathy. And Justin Bieber.
Educators, online or not, don’t compete with each other. They struggle to be noticed in our math-phobic society, where we casually wonder “Should algebra be taught at all?” not “Can algebra be taught better?”.
Entertainment is great; I love Starcraft. But it’s alarming when a prominent learning initiative gets less attention than a throwaway pop song (Super Bass: 268M views in a year; Khan Academy: 175M views in 5 years). Online learning is a rounding error next to Justin Bieber — “Baby” has 700M views alone.
What do we need? The Math Avengers. Different heroes, different tactics, and not without differences… but everyone fighting on the same side. Against Bieber.
I could be walking into a knife fight with an ice cream cone, but I’d like to approach each side with empathy and offer specific suggestions to bridge the gap.
The Big Misunderstanding
Superheroes need a misunderstanding before working together. It’s inevitable, and here’s ours (as a math relationship, of course):
Bad Teacher < Online Learning < Good teacher
The problem is in considering each part separately.
Is Khan Academy (free, friendly, always available) better than a mean, uninformed, or absent teacher? Yes!
Is an engaging human experience better than learning from a computer? Yes!
But, really, the ultimate solution is Online learning + Good Teachers.
Tactics differ, but we can agree on the mission: give students great online resources, and give teachers tools to augment their classroom.
Why Do I Care?
I love learning. Here’s my brief background so you can root out my biases.
I was a good student. I was on the math team and hummed songs like “Life is a sine-wave, I want to de-rive it all night long…”. I drew comics about sine & cosine, the crimefighting duo. You might say I enjoyed math.
I entered college and was slapped in the face by my freshman year math class.
Professors at big universities must know everything, right? If I didn’t get a concept, something must be wrong with me, right?
I had a WWII-era, finish-half-a-proof-in-class, grouch of a teacher. I bombed the midterm and was distressed. Math… I loved math! I didn’t mind difficulties in Physics or Spanish. But math? What I used to sing and draw cartoons about?
Finals came. While cramming, I found notes online, far more helpful than my book and teacher. I sent an email to the class, gingerly suggesting BY EUCLID YOU NEED TO READ THESE WEBSITES THEY ARE SO MUCH BETTER THAN THE PROFESSOR. The websites turned up on an index card in the computer lab that evening. How many of us were struggling?
I was studying, staring at a blue book when an aha! moment struck. I could see the Matrix: equations were a description of twists, turns and rotations. Their meaning became “obvious” in the way a circle must be round. What else could it be?
I was elated and furious: “Why didn’t they explain it like that the first time?!”
Paranoid I’d forget, I put my notes online and they evolved into this site: insights that actually worked for me. Articles on e, imaginary numbers, and calculus became popular — I think we all crave deep understanding. Bad teaching was a burst of gamma rays: I’m normally mild mannered, but enter Hulk Mode when recalling how my passion nearly died.
My core beliefs:
A bad experience can undo years of good ones. Students need resources to sidestep bad teaching.
Hard-won insights, sometimes found after years of teaching, need to be shared
Learning “success” means having basic skills and the passion to learn more. A year, 5 years from now, do people seek out math? Or at least not hate it? (Compare #ihatemath to #ihategeography)
(Oh, I had great teachers too, like Prof. Kulkarni. The bad one just unlocked the Hulk.)
An Open letter to Khan Academy and Teachers
I recently heard a quote about constructive dialog: “Don’t argue the exact point a person made. Consider their position and respond to the best point they could have made.”
Here’s the concerns I see:
Packaging and presentation matters
Yes, other resources and tutorials exist, but there’s power in a giant, organized collection. We visit Wikipedia because we know what to expect, and it’s consistent.
Khan Academy provides consistent, non-judgmental tutorials. There are exercises and discussions for every topic. You don’t need to scour YouTube, digest hour-long calculus lectures, or open up PDF worksheets for practice.
So, let’s use the magic of friendly, exploratory, bite-sized learning of topics.
Community matters
Teachers and online tools don’t “compete” any more than Mr. Rogers and Sesame Street did. They’re both ways to help.
I do think the name “Khan Academy” presents a challenge to community building. Would you rather write for Wikipedia or the Jimmy-Wales-o-pedia?
Wikipedia really feels like a community effort, and though there are alternatives, in general it’s a well-loved resource.
I think teachers may hesitate to use Khan Academy, not out of jealousy, but concern that a single pedagogical approach could overpower all others. Let’s build an online resource that can take input from the math community.
Human interaction matters
It’s easy to misunderstand Khan Academy’s goal. I’ve seen many of their blog posts and videos, and believe Khan Academy wants to work with teachers to promote deep understanding.
But, some news coverage shows students working silently in front of computers in class, not watching at home to free up class time for personal discussions.
The teacher doesn’t appear to be involved or interacting, and that misuse of a learning tool is a nightmare for teachers who want a personal connection. Let’s have an online resource that directly contributes to offline interactions also.
Experience matters
I’ve seen that insights emerge hours (or years) after learning a subject. For example, we’ve “known” since 4th grade what a million and billion are: 1,000,000 and 1,000,000,000.
But do we feel it? How long is a million seconds, roughly? C’mon, guess. Ready? It’s 12 days.
Ok, now how long is a billion seconds? It’s… wait for it… 31 years. 31 years!
That’s the difference between knowing and feeling an idea. Passion comes from feeling.
Teachers draw on years of experience to get ideas to click — let’s feed this back into the online lessons.
Students matter
We teach for the same reason: to help students. Here’s a few specific situations to consider.


For many, Khan Academy is their only positive math experience: not teachers, or peers, or parents, but a video. Sure, it’s not the same as an in-person teacher, but it’s miles beyond an absent or hostile one. If an education experience gets someone excited to learn, and coming back to math, we should celebrate.
Remember, despite years of positive experiences and acing tests, a sufficiently bad class nearly drove me away from math. Resources like Khan Academy offer a lifeline: “Even with a bad teacher, I can still learn”.
When someone is interested, we need to feed their curiosity. I get a lot of traffic from Khan Academy comments — how can we help students dive deeper, without making them trudge randomly through the internet?
Lastly, we all learn differently. I generally prefer text to videos (faster to read, and I can “pause” with my eyes and think). Some like the homemade feel of Khan’s videos. Others might like the polished overviews in MinutePhysics. You might prefer 3-act math stories or modeling instruction.
Let’s offer several types of resources for students to enjoy.
Calling the Math Avengers
Still here? Fantastic. To all teachers, online and non:
- What specific steps can we take to align our efforts?
One idea: Make a curated, collaborative, easy-to-explore teaching resource.
Khan Academy is well-organized: each topic has a video and sample problems. How about sections for complementary teaching styles, projects, and misconceptions?
Imagine a student could select their “Math hero” as Khan Academy or PatrickJMT or James Tanton and see lessons in the style they prefer (like Wikipedia, curate the list to “notable” resources).
Imagine teachers could explore the best in-class activities (“What projects work well for negative numbers?”).
Whatever the style, make it easy for other educators to contribute. Want project-based videos? Sure. Need step-by-step tutorials? Great. Prefer a conceptual overview? No problem.
Each teacher keeps their house style. Let Hulk smash, and Captain America handle the hostage negotiations. Use the hero that suits you.
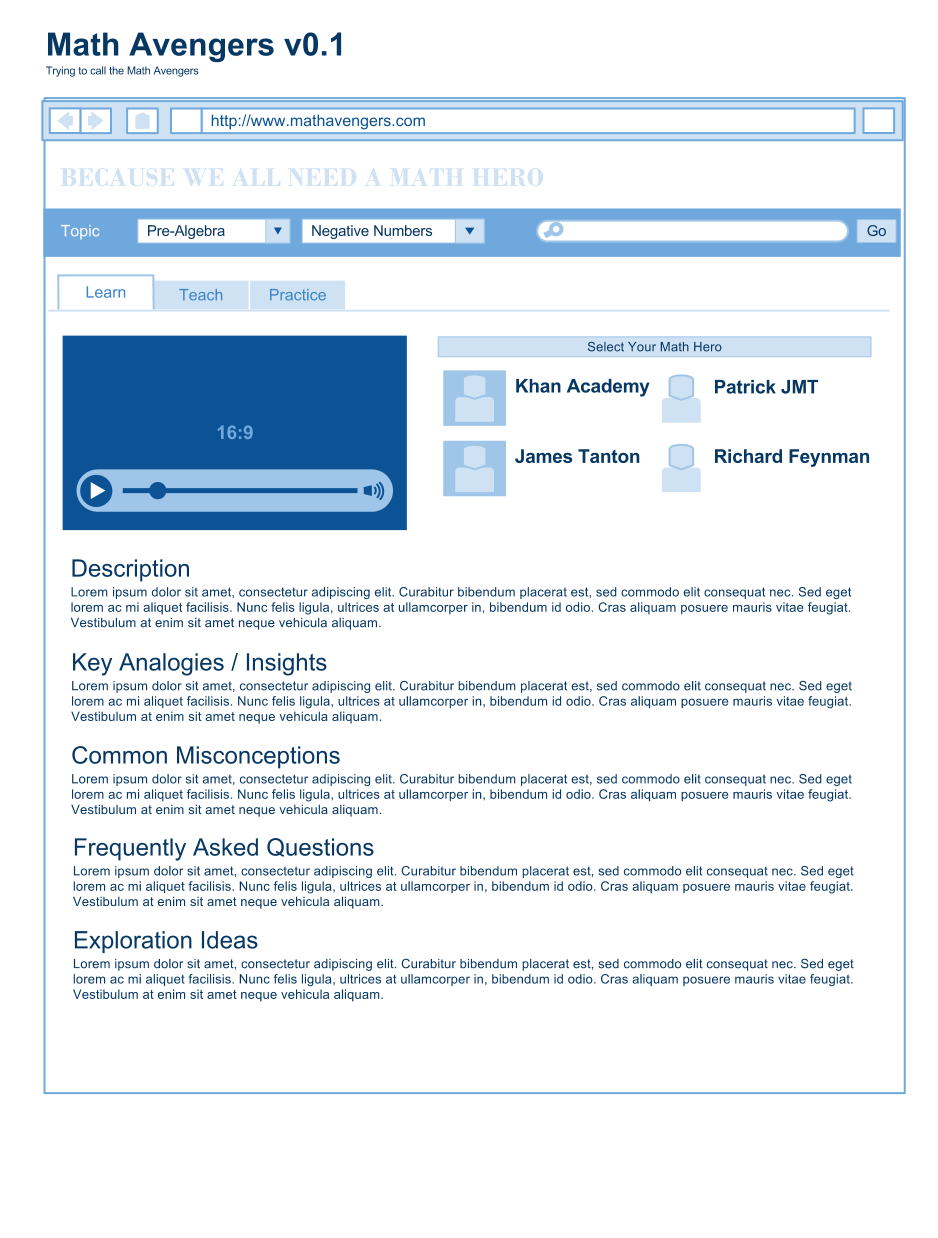
(It’s a public google doc you can copy and edit)
Perfect? Nope. But it’s a starting point to think about how we can work together.
Let’s focus on the overlap and align our efforts: different heroes, different tactics, and on the same side.
Other Posts In This Series
- Developing Your Intuition For Math
- Why Do We Learn Math?
- How to Develop a Mindset for Math
- Learning math? Think like a cartoonist.
- Math As Language: Understanding the Equals Sign
- Avoiding The Adjective Fallacy
- Finding Unity in the Math Wars
- Brevity Is Beautiful
- Learn Difficult Concepts with the ADEPT Method
- Intuition, Details and the Bow/Arrow Metaphor
- Learning To Learn: Intuition Isn't Optional
- Learning To Learn: Embrace Analogies
- Learning To Learn: Pencil, Then Ink
- Learning to Learn: Math Abstraction
- Learning Tip: Fix the Limiting Factor
- Honest and Realistic Guides for Learning
- Empathy-Driven Mathematics
- Studying a Course (Machine Learning) with the ADEPT Method
- Math and Analogies
- Colorized Math Equations
- Analogy: Math and Cooking
- Learning Math (Mega Man vs. Tetris)