Developing Your Intuition For Math

Our initial exposure to an idea shapes our intuition. And our intuition impacts how much we enjoy a subject. What do I mean?

Suppose we want to define a “cat”:

Caveman definition: A furry animal with claws, teeth, a tail, 4 legs, that purrs when happy and hisses when angry…
Evolutionary definition: Mammalian descendants of a certain species (F. catus), sharing certain characteristics…
Modern definition: You call those definitions? Cats are animals sharing the following DNA: ACATACATACATACAT…

The modern definition is precise, sure. But is it the best? Is it what you’d teach a child learning the word? Does it give better insight into the “catness” of the animal? Not really. The modern definition is useful, but after getting an understanding of what a cat is. It shouldn’t be our starting point.

Unfortunately, math understanding seems to follow the DNA pattern. We’re taught the modern, rigorous definition and not the insights that led up to it. We’re left with arcane formulas (DNA) but little understanding of what the idea is.

Let’s approach ideas from a different angle. I imagine a circle: the center is the idea you’re studying, and along the outside are the facts describing it. We start in one corner, with one fact or insight, and work our way around to develop our understanding. Cats have common physical traits leads to Cats have a common ancestor leads to A species can be identified by certain portions of DNA. Aha! I can see how the modern definition evolved from the caveman one.

But not all starting points are equal. The right perspective makes math click — and the mathematical “cavemen” who first found an idea often had an enlightening viewpoint. Let’s learn how to build our intuition.

What is a Circle?

Time for a math example: How do you define a circle?

Definitions of a circle

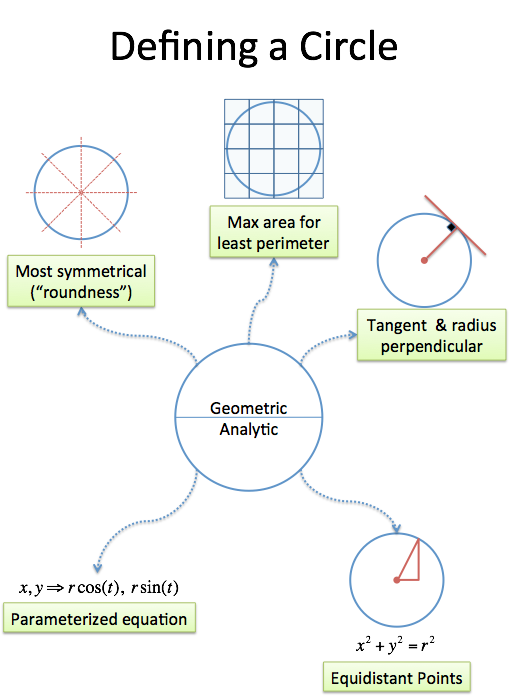
There are seemingly countless definitions. Here’s a few:

The most symmetric 2-d shape possible
The shape that gets the most area for the least perimeter (see the isoperimeter property)
All points in a plane the same distance from a given point (drawn with a compass, or a pencil on a string)
The points (x,y) in the equation x² + y² = r² (analytic version of the geometric definition above)
The points in the equation r* sin(t), r* cos(t), for all t (really analytic version)
The shape whose tangent line is always perpendicular to the position vector (physical interpretation)

The list goes on, but here’s the key: the facts all describe the same idea! It’s like saying 1, one, uno, eins, “the solution to 2x + 3 = 5″ or “the number of noses on your face” — just different names for the idea of “unity”.

But these initial descriptions are important — they shape our intuition. Because we see circles in the real world before the classroom, we understand their “roundness”. No matter what fancy equation we see (x² + y² = r²), we know deep inside that a circle is “round”. If we graphed that equation and it appeared square, or lopsided, we’d know there was a mistake.

As children, we learn the “caveman” definition of a circle (a really round thing), which gives us a comfortable intuition. We can see that every point on our “round thing” is the same distance from the center. x² + y² = r² is the analytic way of expressing that fact (using the Pythagorean theorem for distance). We started in one corner, with our intuition, and worked our way around to the formal definition.

Other ideas aren’t so lucky. Do we instinctively see the growth of e, or is it an abstract definition? Do we realize the rotation of i, or is it an artificial, useless idea?

A Strategy For Developing Insight

I still have to remind myself about the deeper meaning of e and i — which seems as absurd as “remembering” that a circle is round or what a cat looks like! It should be the natural insight we start with.

Missing the big picture drives me crazy: math is about ideas — formulas are just a way to express them. Once the central concept is clear, the equations snap into place. Here’s a strategy that has helped me:

Step 1: Find the central theme of a math concept. This can be difficult, but try starting with its history. Where was the idea first used? What was the discoverer doing? This use may be different from our modern interpretation and application.
Step 2: Explain a property/fact using the theme. Use the theme to make an analogy to the formal definition. If you’re lucky, you can translate the math equation (x^{2 + y}2 = r^2) into a plain-english statement (”All points the same distance from the center”).
Step 3: Explore related properties using the same theme. Once you have an analogy or interpretation that works, see if it applies to other properties. Sometimes it will, sometimes it won’t (and you’ll need a new insight), but you’d be surprised what you can discover.

Let’s try it out.

A Real Example: Understanding e

Understanding the number e has been a major battle. e appears all of science, and has numerous definitions, yet rarely clicks in a natural way. Let’s build some insight around this idea. The following section will have several equations, which are simply ways to describe ideas. Even if the equation is gibberish, there’s a plain-english idea behind it.

Here’s a few popular definitions of e:

Definitions of a circle

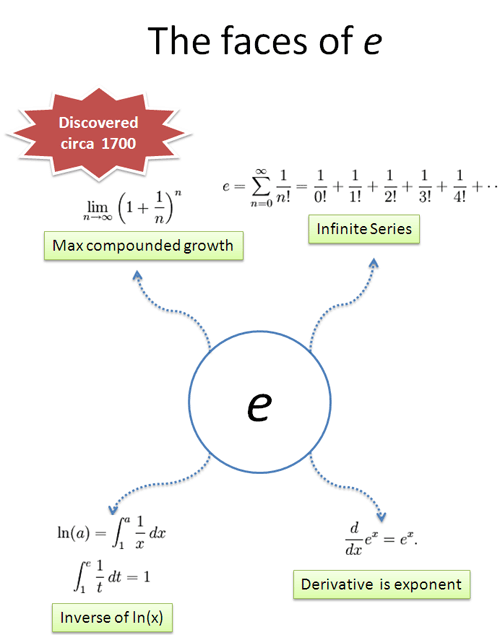
The first step is to find a theme. Looking at e’s history, it seems it has something to do with growth or interest rates. e was discovered when performing business calculations (not abstract mathematical conjectures) so “interest” (growth) is a possible theme.

Let’s look at the first definition, in the upper left. The key jump, for me, was to realize how much this looked like the formula for compound interest. In fact, it is the interest formula when you compound 100% interest for 1 unit of time, compounding as fast as possible.

Definition 1: Define e as 100% compound growth at the smallest increment possible.

The article on e describes this interpretation.

Let’s look at the second definition: an infinite series of terms, getting smaller and smaller. What could this be?

$\displaystyle{e = {1 \over 0!} + {1 \over 1!} + {1 \over 2!} + {1 \over 3!} + \cdots}$

After noodling this over using the theme of “interest” we see this definitions shows the components of compound interest. Now, insights don’t come instantly — this insight might strike after brainstorming “What could 1 + 1 + 1/2 + 1/6 + …” represent when talking about growth?”

Well, the first term (1 = 1/0!, remembering that 0! is 1) is your principal, the original amount. The next term (1 = 1/1!) is the “direct” interest you earned — 100% of 1. The next term (0.5 = 1/2!) is the amount of money your interest made (”2nd level interest”). The following term (.1666 = 1/3!) is your “3rd-level interest” — how much money your interest’s interest earned!

Money earns money, which earns money, which earns money, and so on — the sequence separates out these contributions (read the article on e to see how Mr. Blue, Mr. Green & Mr. Red grow independently). There’s much more to say, but that’s the “growth-focused” understanding of that idea.

Definition 2: Define e by the contributions each piece of interest makes

Neato.

Now to the 3rd, and shortest definition. What does it mean? Instead of thinking “derivative” (which turns your brain into equation-crunching mode), think about what it means. The feeling of the equation. Make it your friend.

$\displaystyle{\frac{d}{dx}Blah = Blah}$

It’s the calculus way of saying “Your rate of growth is equal to your current amount”. Well, growing at your current amount would be a 100% interest rate, right? And by always growing it means you are always calculating interest — it’s another way of describing continuously compound interest!

Definition 3: Define e by as a function always growing by 100% of your current value

Nice — e is the number where you’re always growing by exactly your current amount (100%), not 1% or 200%.

Time for the last definition — it’s a tricky one. Here’s my interpretation: Instead of describing how much you grew, why not say how long it took?

If you’re at 1 and growing at 100%, it takes 1 unit of time to get from 1 to 2. But once you’re at 2, and growing 100%, it means you’re growing at 2 units per unit time! So it only takes 1/2 unit of time to go from 2 to 3. Going from 3 to 4 only takes 1/3 unit of time, and so on.

The time needed to grom from 1 to A is the time from 1 to 2, 2 to 3, 3 to 4… and so on, until you get to A. The first definition defines the natural log (ln) as shorthand for this “time to grow” computation.

ln(a) is simply the time to grow from 1 to a. We then say that “e” is the number that takes exactly 1 unit of time to grow to. Said another way, e is is the amount of growth after waiting exactly 1 unit of time!

Definition 4: Define the time needed to grow continuously from 1 to as ln(a). e is the amount of growth you have after 1 unit of time.

Whablamo! These are four different ways to describe the mysterious e. Once we have the core idea (”e is about 100% continuous growth”), the crazy equations snap into place — it’s “possible” to translate calculus into English. Math is about ideas!

What’s the Moral?

In math class, we often start with the last, most complex idea. It’s no wonder we’re confused — we’re showing DNA and expecting students to see the cat.

I’ve learned a few lessons from this approach, and it underlies how I understand and explain math:

Search for insights and apply them. That first intuitive insight can help everything else snap into place. Start with a definition that makes sense and “walk around the circle” to find others.
Develop mental toughness. Banging your head against an idea is no fun. If it doesn’t click, come at it from different angles. There’s another book, another article, another person who explains it in a way that makes sense to you.
It’s ok to be visual. We think of math as rigid and analytic — but visual interpretations are ok! Do what develops your understanding. Imaginary numbers were puzzling until their geometric interpretation came to light, decades after their initial discovery. Looking at equations all day didn’t help mathematicians “get” what they were about.

Math becomes difficult and discouraging when we focus on definitions over understanding. Remember that the modern definition is the most advanced step of thought, not necessarily the starting point. Don’t be afraid to approach a concept from a funny angle — figure out the plain-English sentence behind the equation. Happy math.

44 Comments

Posted January 8, 2009, under Guides, Math
Tags:
Related Posts:

A BetterExplained Guide To Calculus

Law of Unintended Consequences

About BetterExplained.com

Math, BetterExplained eBook Available!

Navigate a Grid Using Combinations And Permutations

Like it? Share on:

RSS or Email Subscription |

Print This Post

44 Comments »

Trackbacks & Pingbacks

Pingback by Ragged Clown » Blog Archive » Is it a cat? — January 8, 2009 @ 9:51 pm
Pingback by Develop your intuition for maths. | Steve Freeman — January 13, 2009 @ 11:26 am
Pingback by Carnival of Mathematics and other links « The Math Less Traveled — January 18, 2009 @ 9:53 am
Pingback by Bookmarks for January 20th from 21:14 to 21:14 | The PHA — January 20, 2009 @ 11:02 pm
Pingback by 最近的最近 at 奔三 — February 8, 2009 @ 2:46 am

Comments

First of: I really, really like your posts.

I do explain e from the derivative point of view. We encounter it when we’re searching for a formula for derivating exponential functions.
We first investigate using a computer and numerical aproximation what the derivative of a^x is. We easily see that this is a^x times a given constant (c_a). Different a’s yield different constants.
Using the right questions, we come to the point where pupils ask if there’s an a which constant is 1. Meaning de derivative of the function is the function itself.
We first approximate it (trial and error). And then try to find a proper,formal definition (yielding the limit definition)

Peter — January 8, 2009 @ 2:47 pm
@Peter: Thanks for the comment!

I think the approach of starting with the rate of change works too. Pretty much any corner is good, though I’ve yet to see a nice, intuitive explanation starting from the natural log definition and working its way around to e — it just seems too indirect a starting point.

The key is seeing that exponential functions are linked because they change proportional to their current amount. e is like the unit circle where the radius is 1 — other functions are a scaled version of it.

Thanks for leading students through a path that helps build an understanding.

Kalid — January 8, 2009 @ 10:14 pm
Hey Kalid,

Great article! Sometimes I think I should find out all my math teachers from Senior School & Engineering School and make them read your articles. I wish you were one of my teachers! Though now you definitely are!

I really relish your posts and I think you are my first virtual math teacher! … Will definitely like to meet you sometime!

Thanks. Keep up the good work.

Prateek Sharma — January 8, 2009 @ 11:33 pm
I like that explanation of e, but the notion of developing an intuitive idea behind mathematical concepts isn’t new (perhaps it’s because I have a different sense of intuition from most people).
The first thing that young children learn is counting from 1. They start at 1 instead of 0 because it’s considered more intuitive to think of something that’s there rather than something that isn’t. After that, basic arithmetic is taught by the notion of incrementing until students get a ‘feel’ for how much any given number of increments affects a particular number.
I could be wrong about that last part. I think it was that intuition that pushed me to studying math in college, and I definitely know people who never developed that intuition!
But, even when we studied concepts such as derivation- we didn’t just write down the limit definition. We made calculations of slope for very small steps.

Idunno, just something to mull over…

jehan — January 9, 2009 @ 6:17 am
I am a math major and this is right on the dot. There are so many facets of math that unless you do something like this to connect them all, you forget most of it very quickly.

Samson — January 9, 2009 @ 7:54 am
@Prateek: Thanks for the note! Heh, if your old teachers would enjoy it, feel free to send the articles along . And sure, feel free to drop me an email if you’re ever in the Seattle area.

@Jehan: Nope, the idea of using an intuitive approach isn’t new, but I wanted to spread the word. You’re lucky that you were able to start with slopes and work to the limit definition — some people just have limits, epsilons and deltas just thrown at them without any context.

@Samson: Thanks! I agree, if you learn a subject as a set of disconnected facts it becomes easy to forget.

Kalid — January 9, 2009 @ 6:54 pm
I am a second year math teacher and your post help me to better understand the purpose of mathematics and why I strive to teach this way.

Kenny — January 10, 2009 @ 8:40 pm
@Kenny: Thanks for the comment!

Kalid — January 12, 2009 @ 8:15 pm
Thanks for article.

Actually this is not valid only in math, but in all other topics. As an example, we learn forecasting in our production planning course, if you study the history of invention of the theorem, you can understand topic easier.

Cheers.

nanotürkiye — January 15, 2009 @ 1:49 pm
@nanotürkiye: Thanks for the comment! Yes, I very much agree — nearly any subject can be understood at a more intuitive level by looking at its context.

Kalid — January 16, 2009 @ 12:54 pm
determining whether a property of an object is “if and only if”, ie sufficient to define that object, is an important habit to build for a mathematician. however, all of these terms have “canonical” definitions. For example, the set of all points equally distant from a common center was what the term “circle” was invented to refer to.

“we know what a circle is, but how do we define it?” is actually kind of dishonest, viewed in this context. if you know what it is, that knowledge IS the definition.

my two cents, anyway.

misanthropope — January 17, 2009 @ 2:07 am
Is there a “plain English” way to explain e^(i*pi) = -1? To me, this is the most mystifying formula. No amount of staring at De Moivre’s theorem, the series expansion, etc seems to offer any real clarity.

– anon

anon — January 17, 2009 @ 9:35 am
Its always good to see things being explained from a practical point of view; however, if you intend to study math, such a luxury is not always available and so it may not be a good habit to get into.

Instead I believe what is just as instructive as studying an intuitive approach–in terms of insight gained–is showing that a number of definitions are indeed equal by whatever tools are available to you–yes that means epsilon-delta proofs may be necessary. In fact, I would opt for rigorous arguments over intuitive ones as often intuition can be just as damaging as it can be helpful in mathematics.

Instead of teaching intuition I think its much more productive to teach the logic behind the argument.

matt — January 19, 2009 @ 1:01 am
@misanthropope: Interesting point, thanks for the comment. Yes, sometimes a given property can be described as the definition of an item. However, sometimes the reason for picking that particular property can be obscured. In the circle example, I imagine it’s inventor focused on the roundness/symmetry before noticing that all points were the same distance from the center. A better way to phrase “We know what a circle is, but how do we define it” may be “We understand the concept that a circle conveys, but how is it described in math?”

@anon: I think that De Moivre’s/Euler’s identity can be understood intuitively — I’m planning on getting that one eventually .

@matt: Thanks for the note. I think there’s a balance between intuition and rigor. Unfortunately, I think math education has skewed too far on the rigor side (symbol manipulation) while losing the deeper meaning of the meaning of what the equations are trying to convey.

I think it is a cycle though — you use intuition to formulate ideas, rigor to refine and clarify them, intuition to formulate more detailed ideas, rigor to refine those, and so on.

Kalid — January 19, 2009 @ 1:47 am
Great article. In the chemistry course that I’m taking, for example, no one can understand what is being taught because the teacher rarely explains why certain things are true. The only reason why I’m doing well in the class is I take some time to understand what I’ve been told.

For example the order in which electron orbitals fill was simply given to us. I never memorized the order as if it was a new alphabet… I learned the reason why it follows a certain order and produced that sequence to see that indeed I was taught correctly.

Finally, I agree that it is intuition that produces one’s love for a subject. I don’t like mathematics simply because I solve a bunch of problems for homework. I enjoy the subject because I learn more of its secrets with each question that I answer.

Nobody — January 19, 2009 @ 1:58 pm
@Nobody: Thanks for the comment. I totally agree — many subjects come together, and are even fun when understood at an intuitive level.

Kalid — January 22, 2009 @ 5:43 pm
Nice post! One problem is that as a math teacher, one’s instinct is to only say true things… which ironically can get you into real trouble with exposition.

Case in point: me. I read your definition of a circle as the most symmetric 2D shape possible, and immediately started thinking, “but wait, a set of concentric circles is just as symmetric. As is a point. And hey, the entire plane has even more symmetries.”

Then I realized, wow, I shouldn’t be a jerk. Pedantry like mine is exactly the problem you’re complaining about! Thanks for making me take a look at myself.

anonymous — February 1, 2009 @ 5:47 pm
@anonymous: Thanks for the insightful comment! Yes, sometimes the nitty gritty is useful to focus on, but often it can be a hurdle to beginners.

In this context, word “shape” means something along the lines of “a smooth, unbroken convex curve in 2d” which should hopefully eliminate the plane itself and a single point .

Thanks for the comment.

Kalid — February 3, 2009 @ 2:45 am
Hi Kalid,

Thank you kindly for your clear and unobstructed definition of e and ln. Learning basic principles is often very frustrating for maths inept individuals such as myself. I certainly benefit from a simple yet useful explication of what are, at first, abstract topics. Website such as yours have inspired and enabled me to teach myself the very topics from which I once shyed away. Heck, I’m even finding derivatives of complex functions! haha

Thanks again, and please continue to add to your website.

J

J — March 9, 2009 @ 7:31 am
@J: Thanks for the note! Glad you found it helpful and have moved onto doing crazy things like differentiating complex functions . I’ll try to keep the articles coming.

Kalid — March 11, 2009 @ 11:01 pm
hello.im from iran but im human an i have some idea in mathemtic symetry and i play with some formula but i cant now relate theme to a thing please send for me some article about all basic in math please.because i want to study phyzics in the best university with all instrooment for this situation that i want it i most improve very well me math because the mathematics is the base of physics.i read in the petroliom ingeneering in iran in scine and research university but i dont like it im in the end of third year.i want read math in the best university and then study quantom physics in the best univerrsity .here when we say an idea, they laugh.thanks alot and goodbye

seyed amirreza mircheraghi — March 13, 2009 @ 1:23 pm
simple object,great idea!

chaos6174 — April 15, 2009 @ 1:54 am
Great articles you have written. They help me a lot in my quest for understandning mathematics not just “doing it”. Keep up the good work!

Saman — April 22, 2009 @ 2:03 pm
@Seyed: Glad to see you’re interested in education — the articles on the site are what I have now, but Wikipedia and other resources are good jumping off points for more details and references, especially for an area like quantum physics. Good luck.

@Saman: Thanks! Really glad they were useful to you.

Kalid — April 23, 2009 @ 12:21 am
I sumbled upon your site not too long ago but the superb comments made about your posts forced me to read through your posts. You definitely explain things really we’ll. Many people can understand things but cannot explain them well. You understand things very well and you also explain those things very well!

Frank Delano — April 28, 2009 @ 9:06 pm
@Frank: Thank you! I try to explain things as I wish they were taught to me when I was first learning. I’m happy you’re finding the site useful .

Kalid — April 28, 2009 @ 11:06 pm
Sorrym but there are some bad grammar errors in the text, which makes it hard to understand certain things, because first, you have to guess what you could have meant. One example is »We then say that “e” is the number that takes exactly 1 unit of time to grow to.«. To what? The sentence makes no sense.
There are many more such “bugs”. I think your article is pretty nice, but please proofread your texts before posting them.

BAReFOOt — October 16, 2009 @ 12:18 am
Sorry, but there are some bad grammar errors in the text, which makes it hard to understand certain things, because first, you have to guess what you could have meant. One example is »We then say that “e” is the number that takes exactly 1 unit of time to grow to.«. To what? The sentence makes no sense.
There are many more such “bugs”. I think your article is pretty nice, but please proofread your texts before posting them.

BAReFOOt — October 16, 2009 @ 12:19 am
See, that’s the difference between proofreading, and not proofreading.

BAReFOOt — October 16, 2009 @ 12:20 am
Thank you very much for creating this site and for sharing your ideas. I find them very-very helpful. Being a Radio Designer I have to use math/calculus to solve problems every day. Dry/rigorous approach never worked for me. I was “lucky” enough to go through university in very competitive class and our teachers seemed to abuse the idea to explain as little as possible to “make you think” let alone trying to come up with intuitive explanation. The only way to succeed was to come up with my own “theory”. But I have to admit that yours are way better. That’s why I find your articles invaluable. And yes, e bothered me forever, but not anymore .

RF_Guy — October 17, 2009 @ 10:13 am
@RF_Guy: Thanks for the note and encouragement! I’m working through my notes & would love to make a calculus book one day. I’m going back and revisiting concepts I thought I understood, and seeing more and more insights that I completely missed the first time around.

I really agree with you about the need for rigor — it has its place, but more important is to nurture an enthusiasm/enjoyment for the subject. I’ll definitely keep contributing to the site!

Kalid — October 20, 2009 @ 10:22 am
I totally agree with your POV as a struggling math undergrad.
In particular, in the area of Analysis, pedagogy is lacking in the majority of texts.

Hank — December 16, 2009 @ 11:40 am
Hi kalid,

This is a bit long and you may find it amusing or funny but I wrote it straight as i was thinking; I hope you would pardon me and please pardon me!!!
If you recall I had posted a comment earlier mentioning that I go blank while trying to find relationships etc.

Same thing happened again with higher concepts, but one day I recalled that I was doing same thing long time ago while I was in primary school.

(Pardon me coz this may sound childish)
I had rote learned this particular formula :
(a+b)2=a2 + b2 + 2ab (a2 as in a square).

I thought about going to basic and start from top down.. i.e. from formula to history using my imagination.

First que: How does it help? if i know 3 square = 9 & 4 square equals 16.. will this help in getting to know 7 square?

Sec que: How did they arrive at it in first place?

all i could envision (gaphically) was two square boxes. one of length 3 & other of length 4.
Now I moved on to bigger box of length 7 & now I was thinking of relating it to formula & I divided it into two lengths of 3 & 4.

Within this bigger box i could draw area of 3 square & 4 square with there edges meeting at a point inside the 7 square box.

left over areas were two recangles, one had length 3 & breadth 4 while the other had opposite figures… so i could think of graphicall division in terms of area in a plane.

But now I want some input regarding how am I doing and if my directin is correct at all I would to know how ancient engineers could have used these equations to solve what kind of problem?
(BTW i don’t how to post my drawings here so i had to explain them sorry for inconvenience)

Thanks & Regards
hitendra

hitendra — December 18, 2009 @ 5:01 am
@hitendra: Thanks for writing! Yes, I like visualizing the multiplication with the diagram — I think I know what you mean. You can take a square of side 7 (3 + 4) and break it into a 3×3, a 4×4, and two 3×4 rectangles.

In terms of use, it’s a neat algebraic property… some people might think that (3+4)^2 = 3^2 + 4^2 but clearly that is not the case. So when solving any problem with area, it’s important to know the correct result of that equation. In terms of everyday use, let’s see… if you are marking off a square plot of land, it’s better to make one big square (7×7) instead of two smaller ones (3×3 and 4×4), so the king can collect more taxes . Or, if arranging soldiers in a field, and you see an army approaching (7×7) you know your two squadrons (4×4 and 3×3) will not be enough to fight them. I’m stretching here, but algebra is general is pretty useful .

Kalid — December 19, 2009 @ 2:16 am
Hi kalid,
I have arrived at a conclusion that your approach towards learning maths basically encompasses these areas:
1. Philosophy : Observing world as it is without any bias would help us to see shapes, changes in figures that do not naturally tally with our innate logical conclusions or calculations.
2. Abstraction : Once a person identifies a real world problem scenario then he can break it down to simpler and easier to tackle diagrams or figures ( for e.g. straight lines instead of actual continuosly changing landscape).
3. Pattern Finding : This would require collecting abstracts from multiple problem scenarios and finding common link or relationship.
4. Language : Finding or labelling abstractions,patterns and relationship with proper word, and best possible phrases with example for consumption by other people.. i can say communication.
5. Symbolizing & Reduction: Replacing general language statments with symbols as much as possible to reduce ambiguity (Formalism).
6. Rigor : working with Formal methods on huge chunk of data or repeating above steps to make sure proof is strong and is factually correct.

But considering vast requirement of educating childern worldwide, plus geo-political turnmoils that we face; Providing such proper math education seems overwhelmingly mammoth task and extremely difficult to plan and execute.

However, If we find historical concepts difficult to grasp or imagine me thinks that we can start rightway with following generalized method:
Listing out problems that we face today like social, political, infrastructural (we can easily get correct data which is in abundance these days) and applying above listed methods on them.. may be that would bring in faster cognition for 14+ age students (even for adults like me who have missed out an opportunity).

What do you think about that?

Thanks and Regards
hitendra

hitendra — December 27, 2009 @ 11:24 pm
DNA: ACATACATACATACATACATACAT lol

Seamus — January 14, 2010 @ 9:31 pm
@Seamus: Glad you liked it .

Kalid — January 15, 2010 @ 4:36 pm
I just encountered this site tonight, in search of a way to convince a friend that the magic number ‘e’ essentially always represents proportionality when it appears in physical equations, due to the fact that powers of ‘e’ are their own derivatives. Mission accomplished in that regard, but what I found interesting, and that I’d never thought of before (and I’m fifty-something), is the connection of the individual terms in the infinite series for ‘e’ to the integrated compound interest mechanism. Thanks!!

Anonymous — January 22, 2010 @ 7:04 pm
@Anonymous: Awesome, glad you enjoyed it! There are so many things I’m just figuring out after visiting them a second time.

Kalid — January 26, 2010 @ 12:58 pm

RSS feed for comments on this post. TrackBack URI

Have a question? Know an explanation that caused your own a-ha moment? Write about it here.