Why Do We Need Limits and Infinitesimals?

So many math courses jump into limits, infinitesimals and Very Small Numbers (TM) without any context. But why do we care?

Math helps us model the world. We can break a complex idea (a wiggly curve) into simpler parts (rectangles):

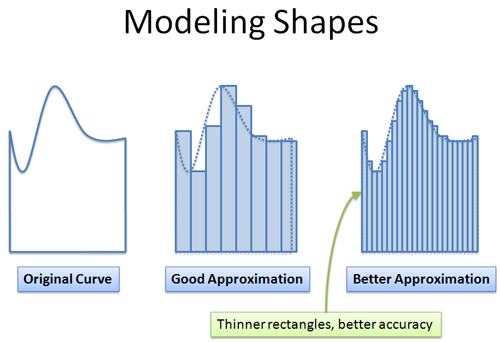
But, we want an accurate model. The thinner the rectangles, the more accurate the model. The simpler model, built from rectangles, is easier to analyze than dealing with the complex, amorphous blob directly.

The tricky part is making a decent model. Limits and infinitesimals help us create models that are simple to use, yet share the same properties as the original item (length, area, etc.).

The Paradox of Zero

Breaking a curve into rectangles has a problem: How do we get slices so thin we don’t notice them, but large enough to “exist”?

If the slices are too small to notice (zero width), then the model appears identical to the original shape (we don’t see any rectangles!). Now there’s no benefit — the ‘simple’ model is just as complex as the original! Additionally, adding up zero-width slices won’t get us anywhere.

If the slices are tiny but measurable, the illusion vanishes. We see that our model is a jagged approximation, and won’t be accurate. What’s a mathematician to do?

We want the best of both: slices so thin we can’t see them (for an accurate model) and slices thick enough to create a simpler, easier-to-analyze model. A dilemma is at hand!

The Solution: Zero is Relative

The notion of zero is biased by our expectations. Is “0 + i”, a purely imaginary number, the same as zero?

Well, “i” sure looks like zero when we’re on the real number line: the “real part” of i, Re(i), is indeed 0. Where else would a purely imaginary number go? (How far East is due North?)

Here’s a different brain bender: did your weight change by zero pounds while reading this sentence? Yes, by any scale you have nearby. But an atomic measurement would show some mass change due to sweat evaporation, exhalation, etc.

You see, there are two answers (so far!) to the “be zero and not zero” paradox:

Allow another dimension: Numbers measured to be zero in our dimension might actually be small but nonzero in another dimension (infinitesimal approach — a dimension infinitely smaller than the one we deal with)
Accept imperfection: Numbers measured to be zero are probably nonzero at a greater level of accuracy; saying something is “zero” really means “it’s 0 +/- our measurement error” (limit approach)

These approaches bridge the gap between “zero to us” and “nonzero at a greater level of accuracy”.

Overview of Limits & Infinitesimals

Let’s see how each approach would break a curve into rectangles:

Limits: “Give me your error margin (I know you have one, you limited, imperfect human!), and I’ll draw you a curve. What’s the smallest unit on your ruler? Inches? Fine, I’ll draw you a staircasey curve at the millimeter level and you’ll never know. Oh, you have a millimeter ruler, do you? I’ll draw the curve in nanometers. Whatever your accuracy, I’m better. You’ll never see the staircase.”
Infinitesimals: “Forget accuracy: there’s an entire infinitely small dimension where I’ll make the curve. The precision is totally beyond your reach — I’m at the sub-atomic level, and you’re a caveman who can barely walk and chew gum. It’s like getting to the imaginary plane from the real one — you just can’t do it. To you, the rectangular shape I made at the sub-atomic level is the most perfect curve you’ve ever seen.”

Limits stay in our dimension, but with ‘just enough’ accuracy to maintain the illusion of a perfect model. Infinitesimals build the model in another dimension, and it looks perfectly accurate in ours.

The trick to both approaches is that the simpler model was built beyond our level of accuracy. We might know the model is jagged, but we can’t tell the difference — any test we do shows the model and the real item as the same.

That trick doesn’t work, does it?

Oh, but it does. We’re tricked by “imperfect but useful” models all the time:

Audio files don’t contain all the information of the original signal. But can you tell the difference between a high-quality mp3 and a person talking in the other room?
Computer printouts are made from individual dots too small to see. Can you tell a handwritten note from a high-quality printout of the same?
Video shows still images at 24 times per second. This “imperfect” model is fast enough to trick our brain into seeing fluid motion.

On and on it goes. We resist because of our artificial need for precision. But audio and video engineers know they don’t need a perfect reproduction, just quality good enough to trick us into thinking it’s the original.

Calculus lets us make these technically imperfect but “accurate enough” models in math.

Working In Another Dimension

We need to be careful when reasoning with the simplified model. We need to “do our work” at the level of higher accuracy, and bring the final result back to our world. We’ll lose information if we don’t.

Suppose an imaginary number (i) visits the real number line. Everyone thinks he’s zero: after all, Re(i) = 0. But i does a trick! “Square me!” he says, and they do: “i * i = -1″ and the other numbers are astonished.

To the real numbers, it appeared that “0 * 0 = -1″, a giant paradox.

But their confusion arose from their perspective — they only thought it was “0 * 0 = -1″. Yes, Re(i) * Re(i) = 0, but that wasn’t the operation! We want Re(i * i), which is different entirely! We square i in its own dimension, and bring that result back to ours. We need to square i, the imaginary number, and not 0, our idea of what i was.

Beware similar mistakes in calculus: we deal with tiny numbers that look like zero to us, but we can’t do math assuming they are (just like treating i like 0). No, we need to “do the math” in the other dimension and convert the results back.

Limits and infinitesimals have different perspectives on how this conversion is done:

Limits: “Do the math” at a level of precision just beyond your detection (millimeters), and bring it back to numbers on your scale (inches)
Infinitesimals: “Do the math” in a different dimension, and bring it back to the “standard” one (just like taking the real part of a complex number; you take the “standard” part of a hyperreal number — more later)

Nobody ever told me: Calculus lets you work at a better level of accuracy, with a simpler model, and bring the results back to our world.

A Real Example: sin(x) / x

Let’s try a conceptual example. Suppose we want to know what happens to sin(x) / x at zero. Now, if we just plug in x = 0 we get a nonsensical result: sin(0) = 0, so we get 0 / 0 which could be anything.

Let’s step back: what does “x = 0″ mean in our world? Well, if we’re allowing the existence of a greater level of accuracy, we know this:

Things that appear to be zero may be nonzero in a different dimension (just like i might appear to be 0 to us, but isn’t)

We’re going to say that x can be really, really close to zero at this greater level of accuracy, but not “true zero”. Intuitively, you can think of x as 0.0000…00001, where the “…” is enough zeros for you to no longer detect the number.

(In limit terms, we say x = 0 + d (delta, a small change that keeps us within our error margin) and in infinitesimal terms, we say x = 0 + h, where h is a tiny hyperreal number, known as an infinitesimal)

Ok, we have x at “zero to us, but not really”. Now we need a simpler model of sin(x). Why? Well, sine is a crazy repeating curve, and it’s hard to know what’s happening. But it turns out that a straight line is a darn good model of a curve over short distances:

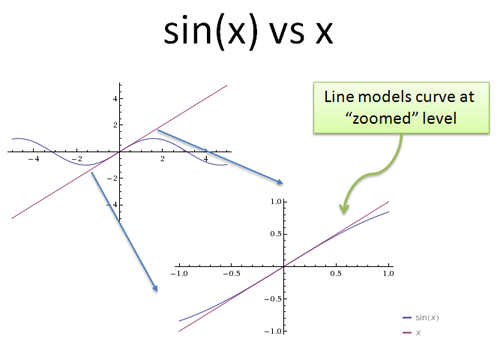
Just like we can break a filled shape into tiny rectangles to make it simpler, we can dissect a curve into a series of line segments. Around 0, sin(x) looks like the line “x”. So, we switch sin(x) with the line “x”. What’s the new ratio?

$\displaystyle{ \frac{\sin(x)}{x} \sim \frac{x}{x} = 1 }$

Well, "x/x" is 1. Remember, we aren’t really dividing by zero because in this super-accurate world: x is tiny but non-zero (0 + d, or 0 + h). When we “take the limit or “take the standard part” it means we do the math (x / x = 1) and then find the closest number in our world (1 goes to 1).

So, 1 is what we get when sin(x) / x approaches zero — that is, we make x as small as possible so it becomes 0 to us. If x became pure, true zero, then the ratio would be undefined (and it is at the infinitesimal level!). But we’re never sure if we’re at perfect zero — something like 0.0000…0001 looks like zero to us.

So, "sin(x)/x" looks like "x/x = 1" as far as we can tell. Intuitively, the result makes sense once we read about radians).

Visualizing The Process

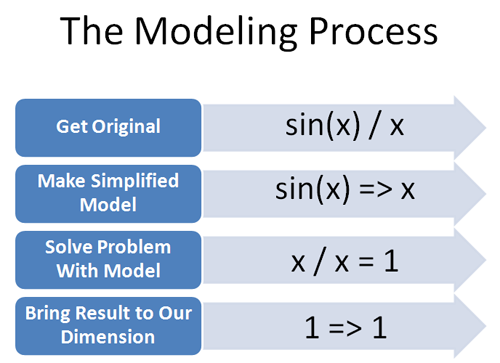
Today’s goal isn’t to solve limit problems, it’s to understand the process of solving them. To solve this example:

Realize x=0 is not reachable from our accuracy; a “small but nonzero” x is always available at a greater level of accuracy
Replace sin(x) by a straight line as a simpler model
“Do the math” with the simpler model (x / x = 1)
Bring the result (1) back into our accuracy (stays 1)

Here’s how I see the process:

In later articles, we’ll learn the details of setting up and solving the models.

Caveats: The Trick Doesn’t Always Work

Some functions are really “jumpy” — and they might differ on an infinitesimal-by-infinitesimal level. That means we can’t reliably bring them back to our world. It looks like the function is unstable at microscopic level and doesn’t behave “smoothly”.

The rigorous part of limits is figuring out which functions behave well enough that simple yet accurate models can be made. Fortunately, most of the natural functions in the world (x, x², sin, e^x) behave nicely and can be modeled with calculus.

Limits Or Infinitesimals?

Logically, both approaches solve the problem of “zero and nonzero”. I like infinitesimals because they allow “another dimension” which seems a cleaner separation than “always just outside your reach”. Infinitesimals were the foundation of the intuition of calculus, and appear inside physics and other subjects that use it.

This isn’t an analysis class, but the math robots can be assured that infinitesimals have a rigorous foundation. I use them because they click for me.

Summary

Phew! Some of these ideas are tricky, and I feel like I’m talking from both sides of my mouth: we want to be simpler, yet still perfectly accurate?

This famous dilemma about “being zero sometimes, and non-zero others” is a famous critique of calculus. It was mostly ignored since the results worked out, but in the 1800s limits were introduced to really resolve the dilemma. We learn limits today, but without understanding the nature of the problem they were trying to solve!

Here are the key concepts:

Zero is relative: something can be zero to us, and non-zero somewhere else
Infinitesimals (“another dimension”) and limits (“beyond our accuracy”) resolve the dilemma of “zero and nonzero”
We create simpler models in the more accurate dimension, do the math, and bring the result to our world
The final result is perfectly accurate for us

My goal isn’t to do math, it’s to understand it. And a huge part of grokking calculus is realizing that simple models created beyond our accuracy can look “just fine” in our dimension. Later on we’ll learn the rules to build and use these models. Happy math.