Calculus examples are boring. "Hey kids! Ever wonder about the distance, velocity, and acceleration of a moving particle? No? Well you're locked in here for 50 minutes!"
I love physics, but it's not the best lead-in. It makes us wait till science class (9th grade?) and worse, it implies calculus is "math for science class". Couldn't we introduce the themes to 5th graders, and relate it to everyday life?
I think so. So here's the goal:
- Use money, not physics, to introduce calculus concepts
- Explore how patterns relate (bank account to salary; salary to raises)
- Use our intuition to explore potential issues (can we keep drilling into patterns?)
Strap on your math helmet, time to dive in.
Money money money
My favorite calculus example is the relationship between your bank account, salary, and raises.
Here's Joe ("Hi, Joe"). You, the sly scoundrel you are, sneak onto Joe's computer and monitor his bank account each week. What can you learn?
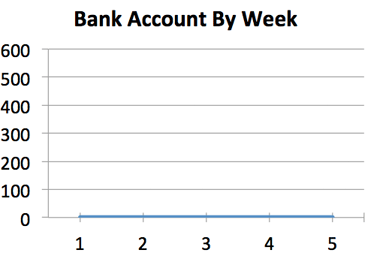
Ack. Clearly, not much happened -- Joe isn't earning anything. And what if you see this?
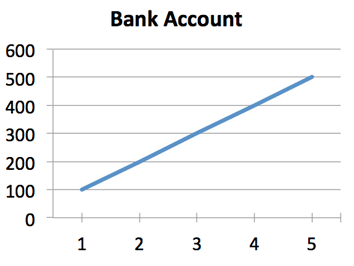
Easy enough: Joe's making some money. And how much? With a quick subtraction, we can figure out his weekly paycheck. Turns out Joe is making a steady \$100/week.
- Key idea: If I know your bank account, I know your salary
The bank account is dependent on the salary -- it changes because of the weekly salary.
Raise the roof
Let's go deeper: knowing the salary, what else can we figure out? Well, the salary is another pattern to analyze -- we can see if it changes! That is, we can tell if Joe's salary is changing week by week (is he getting a raise?).
The process:
- Look at Joe's weekly bank account
- Take the difference in bank account to get the weekly salary
- Take the difference in salary to get the weekly raise (if any)
In the first example \$100/week), it's clear there's no raise (sorry, Joe). The main idea is to "take the difference" to analyze the first pattern (bank account to salary) and "take the difference again" to find yet another pattern (salary to raise).
Working backwards
We just went "down", from bank account to salary. Does it work the other way: knowing the salary, can I predict the bank account?
You're hesitating, I can tell. Yes, knowing Joe gets \$100/week is nice. But... don't we need to know the starting account balance?
Yes! The changes to his account (salary) is not enough -- where did it start? For simplicity (i.e., what you see in homework problems) we often assume Joe starts with \$0. But, if you are actually making a prediction, you want to know the initial conditions (the "+ C").
A More Complex Pattern
Let's say Joe's account grows like this: 100, 300, 600, 1000, 1500...
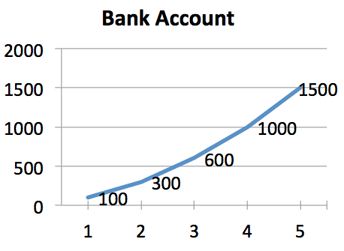
What's going on? Is it random? Well, we can do our week-by-week subtraction to get this:
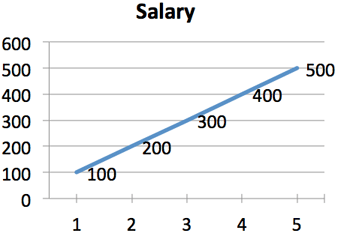
Interesting -- Joe's income is changing each week. We do another week-by-week difference and get this:
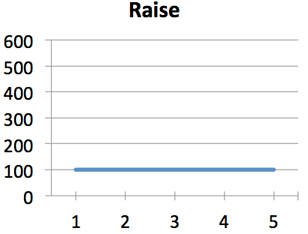
And yep, Joe's getting a steady raise of \$100/week. Let's get wild and chart them on the same graph:
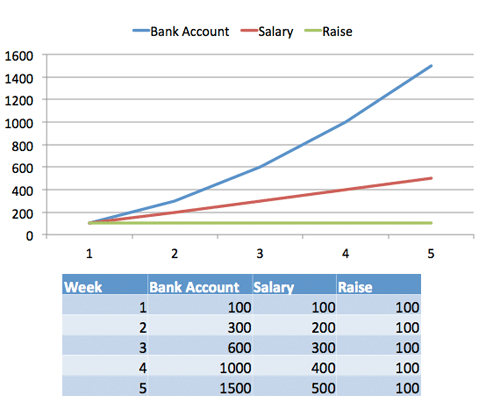
One way to think about it: Joe gets a raise each week, which changes his salary, which changes his bank account. As the raises continue to appear, his salary continues to increase and his bank account rises. You can almost think of the raise "pushing up" the salary, which "pushes up" the bank account.
So... Where's the Calculus?
What's the formula for Joe's bank account for any week? Well, it's the sum of his salaries up to that point:
100 + 200 + 300 + 400... = 100 * n * (n + 1)/2
The formula for adding up a series of numbers (1 + 2 + 3 + 4...) is very close to n^2/2, and gets closer as the number of steps increases.
This is our first "calculus" relationship:
- A constant raise \$100/week) leads to a...
- Linear increase in salary (100, 200, 300, 400) which leads to a...
- Quadratic (something * n^2) increase in bank account (100, 300, 600, 1000... you see it curve!)
Now, why is it roughly 1/2 * n2 and not n2? One intuition: The linear increase in salary (100, 200, 300) gives us a triangle. The area of the triangle represents all the payments so far, and the area is 1/2 * base * height. The base is n (the number of weeks) and the height (income) is 100 * n.
Geometric arguments get more difficult in higher dimensions -- just because we can work out 2*100 with addition doesn't mean it's the easiest way. Calculus gives us the rules to jump between patterns (taking derivatives and integrals).
Points to Explore
Our understanding of bank accounts, salaries, and raises lets us explore deeper.
Could we figure out the total earnings between weeks 1 and 10?
Sure! There's two ways: we could add up our income for each week (week 1 salary + week 2 salary + week 3 salary...) or just subtract the bank account (Week 10 bank account - week 1 bank account). This idea has a beefy name: the Fundamental Theorem of Calculus!
Can we keep going "down" (taking derivatives) beyond the raise?
Well, why not? If the raise is \$100/week, if we take the difference again we see it drops to 0 (there is no "raise raise", aka the raise is always steady). But, we can imagine the case where the raise itself is raising (week1 raise = 100, week2 raise = 200). Using our intuition: if the "raise raise" is constant, the raise is linear (something * n), the income is quadratic (something * n2) and the bank account is cubic (something * n3). And yes, it's true!
Can derivatives go on forever?
Yep. Maybe the connection is bank account => salary => raise => inflation => milk output of Farmer Joe's cow => how much Joe feeds the cow each week. Many patterns "stop having derivatives" once we get to the root cause. But certain interesting patterns, like exponential growth, have an infinite number of components! You have interest, which earns interest, which earns interest, which earns interest... forever! You can never find the single "root cause" of your bank account because an infinite number of components went into it (pretty trippy).
What happens if the raise goes negative?
Interesting question. As the raise goes negative, his salary will start lowering. But, as long as the salary is above zero, the bank account will keep rising! After all, going from \$200 to \$100 per week, while bad to you, still helps your bank account. Eventually, a negative raise will overpower the salary, making it negative, which means Joe is now paying his employer. But up until that point, Joe's bank account would be growing.
How quickly can we check for differences?
Suppose we're measuring a stock portfolio, not a bank account. We might want a second-by-second model of our salary and account balance. The idea is to measure at intervals short enough to get the detail we need -- a large aspect of calculus is deciding what "limit" is enough to say "Ok, this is accurate enough for me!".
The calculus formulas you typically see (integral of x = 1/2 * x^2) are different from the "discrete" formulas (sum of 1 to n = 1/2 * n * (n + 1)) because the discrete case is using "chunky" intervals.
Key Takeaways
Why do I care about the analogy used? The traditional "distance, velocity, acceleration" doesn't lead to the right questions. What's the next derivative of acceleration? (It's called "jerk", and it's rarely used). Such a literal example is like having kids think multiplication is only for finding area, and only works on two numbers at a time.
Here's the key points:
- Calculus helps us find related patterns (bank account, to salary, to raises)
- The "derivative" is going "down" (finding week-by-week changes to get your salary)
- The "integral" is going "up" (adding up your salary to get your bank account)
- We can figure out a formula for a pattern (given my bank account, predict my salary) or get a specific value (what's my salary at week 3?)
- Calculus is useful outside the hard sciences. If you have a pattern or formula (production rate, size of a population, GDP of a country) and want to examine its behavior, calculus is the tool for you.
- Textbook calculus involves memorizing the rules to derive and integrate formulas. Learn the basics (x^n, e, ln, sin, cos) and leave the rest to machines. Our brainpower is better spent learning how to translate our thoughts into the language of math.
In my fantasy world, derivatives and integrals are just two everyday concepts. They're "what you can do" to formulas, just like addition and subtraction are "what you can do" to numbers.
"Hey kids, we find the total mass using addition (Mass1 + Mass2 = Mass3). And to find out how our position changes, we use the derivative".
"Duh -- addition is how you combine stuff. And yeah, you take the derivative to see how your position is changing. What else would you do?"
One can always dream. Happy math.
PS. Want more?
- I have another visual introduction to calculus in terms of shapes
- Learn to see integration as a better multiplication
Other Posts In This Series
- A Gentle Introduction To Learning Calculus
- Understanding Calculus With A Bank Account Metaphor
- Prehistoric Calculus: Discovering Pi
- A Calculus Analogy: Integrals as Multiplication
- Calculus: Building Intuition for the Derivative
- How To Understand Derivatives: The Product, Power & Chain Rules
- How To Understand Derivatives: The Quotient Rule, Exponents, and Logarithms
- An Intuitive Introduction To Limits
- Intuition for Taylor Series (DNA Analogy)
- Why Do We Need Limits and Infinitesimals?
- Learning Calculus: Overcoming Our Artificial Need for Precision
- A Friendly Chat About Whether 0.999... = 1
- Analogy: The Calculus Camera
- Abstraction Practice: Calculus Graphs
- Quick Insight: Easier Arithmetic With Calculus
- How to Add 1 through 100 using Calculus
- Integral of Sin(x): Geometric Intuition