Prehistoric Calculus: Discovering Pi

Pi is mysterious. Sure, you “know” it’s about 3.14159 because you read it in some book. But what if you had no textbooks, no computers, and no calculus (egads!) — just your brain and a piece of paper. Could you find pi?

Archimedes found pi to 99.9% accuracy 2000 years ago — without decimal points or even the number zero! Even better, he devised techniques that became the foundations of calculus. I wish I learned his discovery of pi in school — it helps us understand what makes calculus tick.

How do we find pi?

Pi is the circumference of a circle with diameter 1. How do we get that number?

Say pi = 3 and call it a day.
Draw a circle with a steady hand, wrap it with string, and measure with your finest ruler.
Use door #3

What’s behind door #3? Math!

How did Archimedes do it?

Archimedes didn’t know the circumference of a circle. But he didn’t fret, and started with what he did know: the perimeter of a square. (He actually used hexagons, but squares are easier to work with and draw, so let’s go with that, ok?).

We don’t know a circle’s circumference, but for kicks let’s draw it between two squares:

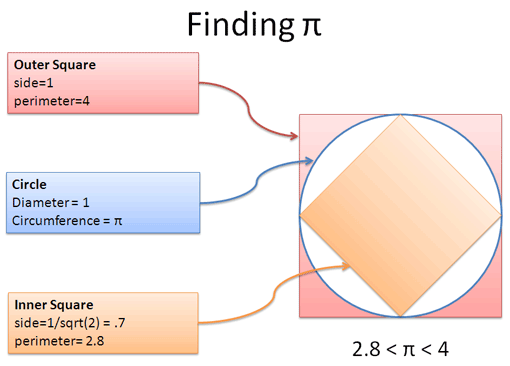
Neat — it’s like a racetrack with inner and outer edges. Whatever the circumference is, it’s somewhere between the perimeters of the squares: more than the inside, less than the outside.

And since squares are, well, square, we find their perimeters easily:

Outside square (easy): side = 1, therefore perimeter = 4
Inside square (not so easy): The diagonal is 1 (top-to-bottom). Using the Pythagorean theorem, side² + side² = 1, therefore side = $\sqrt{1/2}$ or side = .7. The perimeter is then .7 * 4 = 2.8.

We may not know where pi is, but that critter is scurrying between 2.8 and 4. Let’s say it’s halfway between, or pi = 3.4.

Squares drool, octagons rule

We estimated pi = 3.4, but honestly we’d be better off with the ruler and string. What makes our guess so bad?

Squares are clunky. They don’t match the circle well, and the gaps make for a loose, error-filled calculation. But, increasing the sides (using the mythical octagon, perhaps) might give us a tighter fit and a better guess (image credit):

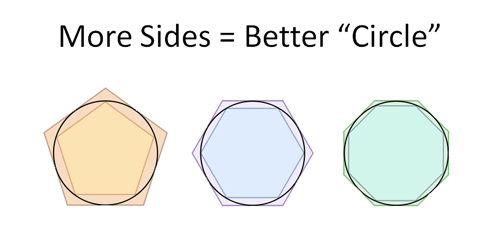
Cool! As we yank up the sides, we get closer to the shape of a circle.

So, what’s the perimeter of an octagon? I’m not sure if I learned that formula. While we’re at it, we could use a 16-side-a-gon and a 32-do-decker for better guesses. What are their perimeters again?

Crickey, those are tough questions. Luckily, Archimedes used creative trigonometry to devise formulas for the perimeter of shape when you double the number of sides:

Inside perimeter: One segment of the inside (such as the side of a square) is sin(x/2), where x is the angle spanning a side. For example, one side of the inside square is sin(90/2) = sin(45) ~ .7. The full perimeter is then 4 * .7 = 2.8, as we had before.

Outside perimeter: One segment of the outside is tan(x/2), where x is the angle spanning one side. So, one segment of the outside perimeter is tan(45) = 1, for a total perimeter of 4.

Neat — we have a simple formula! Adding more sides makes the angle smaller:

Squares have an inside perimeter of 4 * sin(90/2).
Octogons have eight 45-degree angles, for an inside perimeter of 8 * sin(45/2).

Try it out — a square (sides=4) has 91% accuracy, and with an octagon (sides=8) we jump to 98%!

But there’s a problem: Archimedes didn’t have a calculator with a “sin” button! Instead, he used trig identities to rewrite sin and tan in terms of their previous values:

New outside perimeter (harmonic mean): $\displaystyle{\text{newOut} = \frac{2}{\frac{1}{\text{Inside}} + \frac{1}{\text{Outside}} }}$

New inside perimeter (geometric mean): $\displaystyle{\text{newIn} = \sqrt{\text{Inside} \cdot \text{newOut}}}$

These formulas just use arithmetic — no trig required. Since we started with known numbers like $\sqrt{2}$ and 1, we can repeatedly apply this formula to increase the number of sides and get a better guess for pi.

By the way, those special means show up in strange places, don’t they? I don’t have a nice intuitive grasp of the trig identities involved, so we’ll save that battle for another day.

Cranking the formula

Starting with 4 sides (a square), we make our way to a better pi (download the spreadsheet):

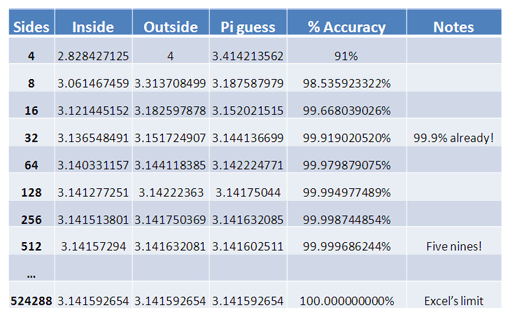
Every round, we double the sides (4, 8, 16, 32, 64) and shrink the range where pi could be hiding. Let’s assume pi is halfway between the inside and outside boundaries.

After 3 steps (32 sides) we already have 99.9% accuracy. After 7 steps (512 sides) we have the lauded “five nines”. And after 17 steps, or half a million sides, our guess for pi reaches Excel’s accuracy limit. Not a bad technique, Archimedes!

Unfortunately, decimals hadn’t been invented in 250 BC, let alone spreadsheets. So Archimedes had to slave away with these formulas using fractions. He began with hexagons (6 sides) and continued 12, 24, 48, 96 until he’d had enough (ever try to take a square root using fractions alone?). His final estimate for pi, using a shape with 96 sides, was:

$\displaystyle{3 \frac{10}{71} < \pi < 3 \frac{1}{7}}$

The midpoint puts pi at 3.14185, which is over 99.9% accurate. Not too shabby!

If you enjoy fractions, the mysteriously symmetrical 355/113 is an extremely accurate (99.99999%) estimate of pi and was the best humanity had for nearly a millennium.

Some people use 22/7 for pi, but now you can chuckle “Good grief, 22/7 is merely the upper bound found by Archimedes 2000 years ago!” while adjusting your monocle. There’s even better formulas out there too.

Where’s the Calculus?

Archimedes wasn’t “doing calculus” but he laid the groundwork for its development: start with a crude model (square mimicking a circle) and refine it.

Calculus revolves around these themes:

We don’t know the answer, but we’ve got a guess. We had a guess for pi: somewhere between 2.8 and 4. Calculus has many concepts such as Taylor Series to build a guess with varying degrees of accuracy.
Let’s make our guess better. Archimedes discovered that adding sides made a better estimate. There are numerical methods to refine a formula again and again. For example, computers can start with a rough guess for the square root and make it better (faster than finding the closest answer from the outset).
You can run but not hide. We didn’t know exactly where pi was, but trapped it between two boundaries. As we tightened up the outside limits (pun intended), we knew pi was hiding somewhere inside. This is formally known as the Squeeze Theorem.
Pi is an unreachable ideal. Finding pi is a process that never ends. When we see π it really means "You want perfection? That's nice -- everyone wants something. Just start cranking away and stop when pi is good enough.".

I’ll say it again: Good enough is good enough. A shape with 96 sides was accurate enough for anything Archimedes needed to build.

The idea that “close counts” is weird — shouldn’t math be precise? Math is a model to describe the world. Our equations don’t need to be razor-sharp if the universe and our instruments are fuzzy.

Life Lessons

Even math can have life lessons hidden inside. Sometimes the best is the enemy of the good. Perfectionism (“I need the exact value of pi!”) can impede finding good, usable results.

Whether making estimates or writing software, perhaps you can start with a rough version and improve it over time, without fretting about the perfect model (it worked for Archimedes!). Most of the accuracy may come from the initial stages, and future refinements may be a lot of work for little gain (the Pareto Principle in action).

Ironically, the “crude” techniques seen here led to calculus, which in turn led to better formulas for pi.

Math Lessons

Calculus often lacks an intuitive grounding — we can count apples to test arithmetic, but it’s hard to think about abstract equations that are repeatedly refined.

Archimedes’ discovery of pi is a vivid, concrete example for our toolbox. Just like geometry refines our intuition about lines and angles, calculus defines the rules about equations that get better over time. Examples like this help use intuition as a starting point, instead of learning new ideas in a vacuum.

Later, we’ll discuss what it means for numbers to be “close enough”. Just remember that 96 sides was good enough for Archimedes, and half a million sides is good enough for Excel. We’ve all got our limits.