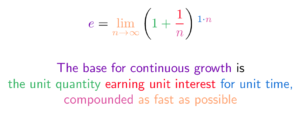E (Compound Interest Definition)

Colorized Definition

\newcommand{\growth}{\color{c1}}
\newcommand{\unitQuantity}{\color{c2}}
\newcommand{\unitInterest}{\color{c3}}
\newcommand{\unitTime}{\color{c4}}
\newcommand{\perfectly}{\color{c5}}
\newcommand{\compounded}{\color{c6}}



\growth       The base for continuous growth
\plain        is
\
\unitQuantity the unit quantity
\unitInterest earning unit interest
\unitTime     for unit time,
\
\compounded   compounded
\perfectly    as fast as possible

Plain English

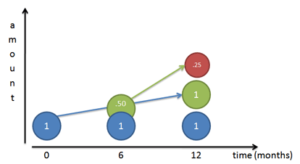
• What is e? A constant (2.718...) representing continuous unit growth: the unit quantity (1.0), continuously growing the unit rate (100%), for unit time (1 period).

• Why's e special? All circles are the unit circle, scaled up. All continuously growing systems are e^{rt}, scaled to some rate and time.

• When should I use e? Use e^{rt} for things that change constantly (radioactive decay, populations). For growth based on discrete intervals (interest payments, combinatorics), (1 + rate)^{time} is a better model.