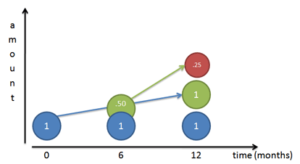
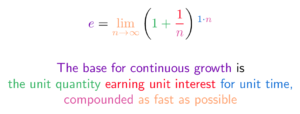E (Natural Log Definition)
Colorized Definition
_4.png)
## Read More
- [An Intuitive Guide To Exponential Functions & e](https://betterexplained.com/articles/an-intuitive-guide-to-exponential-functions-e/)
- [Common Definitions of e (Colorized)](https://betterexplained.com/articles/definitions-of-e-colorized/)
- [Demystifying the Natural Logarithm](https://betterexplained.com/articles/demystifying-the-natural-logarithm-ln/)