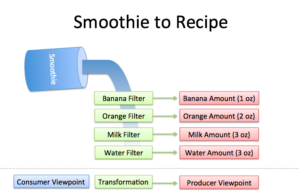
Fourier Transform
Colorized Definition
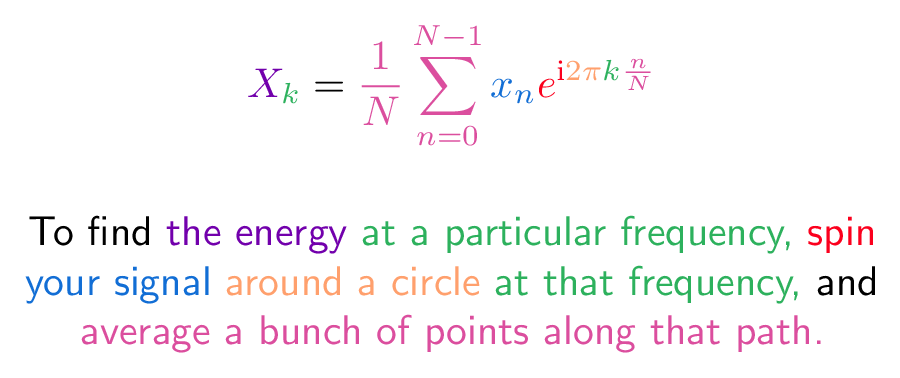
Plain English
What does the Fourier Transform do? Given a smoothie, it finds the recipe.
How? Run the smoothie through filters to extract each ingredient.
Why? Recipes are easier to analyze, compare, and modify than the smoothie itself.
How do we get the smoothie back? Blend the ingredients.
## Read More
- [Interactive Guide to the Fourier Transform](https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/)
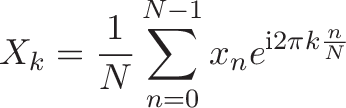 \plain To find
\energy the energy
\freq at a particular frequency,
\spin spin
\
\signal your signal
\Circle around a circle
\freq at that frequency,
\plain and
\
\average average a bunch of points along that path.
\plain To find
\energy the energy
\freq at a particular frequency,
\spin spin
\
\signal your signal
\Circle around a circle
\freq at that frequency,
\plain and
\
\average average a bunch of points along that path.