Imaginary Number
Colorized Definition
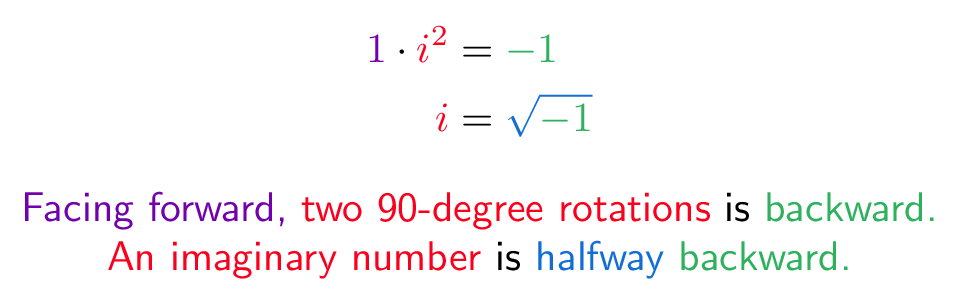
Plain English
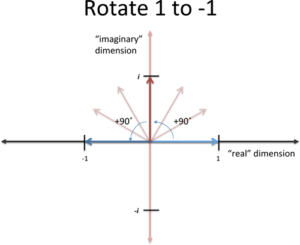
What's an imaginary number? A number pointing sideways (North/South) isntead of the typical East/West number line. ("Imaginary" was a derogatory name from critics, Gauss wanted them called "lateral" numbers.)
What does i mean? i, by itself, points North. Multiplying by i rotates you 90 degrees. 2 rotations points you backwards (i * i = -1), 4 rotations spins you around fully (i^4 = 1).
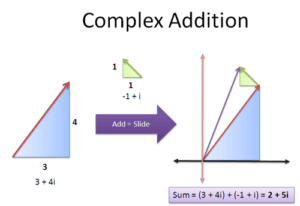
Is i useful? The second dimension is useful, right? Imaginary numbers make 2d rotation problems simple.
## Read More
- [A visual, intuitive guide to imaginary numbers](https://betterexplained.com/articles/a-visual-intuitive-guide-to-imaginary-numbers/)