Summary: Check out the Calculus Learning Guide. I'm sharing an honest, realistic learning plan for what helped me enjoy the subject.
If you want a path that doesn't expect perfect motivation, shares insights in minutes (not weeks), and aims for lifelong insight, this guide is for you.
First Principles of Education
My learning strategy is to ask honest (sometimes uncomfortable) questions about what's really working.
No games, no kidding ourselves, just:
- Did the concept I'm learning click?
- If not, can I find a better explanation? (And let's share it.)
Here's my wishlist for a learning guide. Elon Musk talks about thinking from first principles, starting with fundamental truths and working forward from there1. Who cares what's being done now, what's our goal?
Principle: Avoid teaching hatred of a subject
Priority #1 for any class is: Do not create hate for the subject.
Imagine 99% of people in a skiing class never ski again. They cringe at the thought. We wouldn't console ourselves thinking "Oh, skiing teaches important physical skills that apply to other fields." We'd think "That skiing class is awful and needs to change."
Sure, not everyone will love skiing (or cooking, or math), but they shouldn't detest it. Temporary understanding is not worth permanent aversion.
So, what Calculus introduction made me excited to learn more?
For me, it was seeing how patterns can be cleverly split and re-assembled:
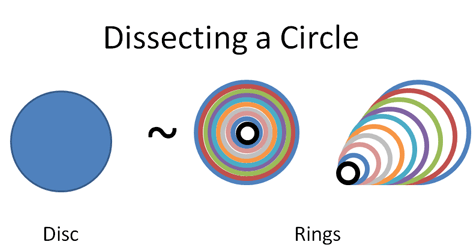
Most courses march you through weeks of theory "appreciate" these diagrams in week 11. Ugh. The big picture helps me appreciate the details, not the reverse.
Principle: Give Realistic Advice
A typical discussion:
"I want to learn Calculus. What should I do?"
"Here's a [full book/course/MOOC]. It's months of effort, I didn't do it myself, but here you go."
In other words, "go the library and read for 100 hours". The real question:
I'm interested in the subject. Is there a plan that worked for you?
Motivation is limited. Traditional classes "work" -- because students are under immense pressure to finish (tuition, peer pressure, fear of not graduating).
Online courses without this pressure have single-digit completion rates. We can pretend students "got something" from the experience, just like you "got something" from a movie you walked out of. We can't change the goalposts to "something is better than nothing" halfway through.
Realistic advice on what worked with my limited motivation (even as a math hobbyist!) is:
Get an Aha! moment in minutes that motivates me to keep going (a cool diagram, example, or simulation).
Take a progressive journey where even if I stop after an hour, I have some helpful insights (vs. an hour of stretching in the parking lot).
Maintain a desire to revisit the subject by having an approachable, gentle introduction. I'll then keep coming back to fill in gaps over time.
Principle: Don't Ignore Difficulties
For fun, find a lesson on imaginary numbers.
Does it acknowledge negative numbers were also distrusted?
Is the name "imaginary" described as an insult, given by people who didn't understand the concept?
Does the teacher mention their own confusion? (Or did imaginary numbers just click?)
Is there a real-world application? (If not, is this because it truly doesn't exist, we haven't tried to look, or it isn't important for learning?)
This type of lesson is a giant pet peeve. The flow is "Here's a confusing concept. I was confused myself, but I won't tell you that. Memorize the definition, apply it in these practice problems, and we'll call it a day."
Argh, this drives me nuts. It reinforces the stereotype that math class is a game of moving symbols around. (This symbol multiplied by this other symbol makes -1. Tada!)
It's ok to lack an intuition; I lack it for most things. But hiding our initial confusion implies the subject isn't confusing.
Principle: Expect to get it wrong sometimes
There's a common trope of the smart-aleck student trying to "outsmart" the teacher. Do basketball players try to "outsmart" their coach?
The flawed assumption is teachers must be some omniscient authority giving you access to precious knowledge. The knowledge is out there, it's not like the teacher invented the math herself. Instead, imagine a coach who is trying to improve your understanding.
Coaches can be wrong, sure. But they've seen many struggle with the same issues you're facing, and are trying to help. It's ok if Lebron James can dunk better than his coach.
The math may be perfect and unchanging, but the way it's taught is not. Let's make it easy to improve lessons and not expect perfection the first time.
Principle: We have Different Goals
Most courses assume you want mastery of the subject. That's fine, but is it necessary?
There are several levels of music understanding:
Intuitive Appreciation: Just enjoying the music.
Natural Description: Humming a tune you heard or made up.
Symbolic Description: Reading and writing the sheet music.
Theory: Explaining how harmonies work, why minor scales are somber, etc.
Performance: Playing the official instruments.
In language learning, there is an ILR scale from no profiency to native fluency. Not everyone studying Calculus needs to become Isaac Newton. Can we have a path that goes as far as we need?
An Honest and Realistic Learning Plan
Combining these insights, I've made a Calculus Learning Guide.
The principles, as I tried to apply them:
It's honest. It's the explanation that actually inspired me, not the theoretical explanation that requires weeks of discipline for some future payoff.
It acknowledges limited motivation. How far can you get in 1 minute? 10 minutes? An hour? Pretty far, I think. And getting a win in 10 minutes means you'll come back for more.
It's updatable. With lessons based primarily on text, we can easily update, re-arrange, add, edit, fix. Other formats are essentially a bet we got it right the first time.
It acknowledges levels of understanding. Most people just want an appreciation for Calculus. Technical performance is a goal we can separate, organize, and build a path to.
I eat the veggies myself. This guide has "gut checks" like "Can I describe an integral in everyday terms?" and "Can I derive the product rule on my own?". This is how I actually refresh my Calculus understanding.
In my ideal world, every Wikipedia topic would have a guide that took you from the 1-minute version to a full technical understanding. Go as far as you wish, make meaningful progress at each step, and have fun along the way.
Happy math.
-
Musk mentions not "reasoning by analogy", or assuming a conclusion is true based on what happened in another scenairo. This is different from "understand by analogy", getting the gist of an idea and then working to the technical version. The analogy is a raft to cross the river, to be left behind once you're on land. ↩
Other Posts In This Series
- Developing Your Intuition For Math
- Why Do We Learn Math?
- How to Develop a Mindset for Math
- Learning math? Think like a cartoonist.
- Math As Language: Understanding the Equals Sign
- Avoiding The Adjective Fallacy
- Finding Unity in the Math Wars
- Brevity Is Beautiful
- Learn Difficult Concepts with the ADEPT Method
- Intuition, Details and the Bow/Arrow Metaphor
- Learning To Learn: Intuition Isn't Optional
- Learning To Learn: Embrace Analogies
- Learning To Learn: Pencil, Then Ink
- Learning to Learn: Math Abstraction
- Learning Tip: Fix the Limiting Factor
- Honest and Realistic Guides for Learning
- Empathy-Driven Mathematics
- Studying a Course (Machine Learning) with the ADEPT Method





Leave a Reply
22 Comments on "Honest and Realistic Guides for Learning"
Kalid,
You are a genius!!
John
Glad you enjoyed it John!
Your work is so cool. I can not thank you enough.
“In my ideal world, every Wikipedia topic would have a guide that took you from the 1-minute version to a full technical understanding. Go as far as you wish, make meaningful progress at each step, and have fun along the way.”
This would be pretty cool. Hope wikipedia has a simple summary first intead of the heavv jargon, technical words it uses to sound so smart
Yep, often times it’s written for someone who already knows the material. I’m hoping to take a crack at topics one by one. (Some ideas for collaboration down the line. Been a long-running goal of mine to make that easier to manage.)
Kalid, do you plan to mount a project at Wikipedia (or elsewhere) to create insightful guides to maths topics? If so, let me know and I’d be happy to join in!
And yes, I do know how much _invisible_ work this kind of writing takes. But I’m up for a challenge!
Of course, BetterExplained is the nearest thing to such a project that I’ve seen yet!
Speaking of Wiki, I have a funny example just yesterday. I was looking for explanation about how “phonograph” works (right, I don’t know how sound is recorded!!!!). And the mechanical components have “cylinder” which everyone knows what it is, I accidently clicked on it and ended up with pieces I have no clue what I am reading about, let’s take a look together:
——————————————————————————
In its simplest form, a cylinder (from Greek κύλινδρος – kulindros, “roller, tumbler”[1]) is the surface formed by the points at a fixed distance from a given straight line called the axis of the cylinder. It is one of the most basic curvilinear geometric shapes.
———————————————————————————
Omg, it turns some stuff which everyone knows about into something completely not recognizable. Imagine what if you are trying to learn something new, something that’s not everyday object and you want to resort to a place to give you an idea!
And again yesterday, I saw a nice explanation of “decibel” (right, I heard about it, don’t know what the hell it is actually, is it force?length?area? good? bad? ). I saw finally one nice concise explanation: it is just measuring air pressure, unit is newton/square meter! And you scale it by log…. That’s it?
Now let’s look at what wiki does:
————————————————————————————————-
The decibel (dB) is a logarithmic unit used to express the ratio of two values of a physical quantity, often power or intensity. One of these values is often a standard reference value, in which case the decibel is used to express the level of the other value relative to this reference. The number of decibels is ten times the logarithm to base 10 of the ratio of two power quantities,[1] or of the ratio of the squares of two field amplitude quantities. One decibel is one tenth of one bel, named in honor of Alexander Graham Bell; however, the bel is seldom used.
More blah blah blah……………… two more paragraphs….
————————————————————————————————————–
This is a frustrating way to learn things!!!
Great example. Argh, the complexity of some Wikipedia explanations kills me. Most references are used to remember something you’ve forgotten, not learn something new.
On learning, an another important point is usually under-emphasized.
There are stupid analogies, stories and pictures in teaching. [Like (Stupid story)”a goes around r and tells that his pies are squared, thus a is pi*r*r” [Taken from “Lockhart’s lament”, a very interesting piece ridiculing math communication] , (Stupid pictures) Symbols as mental pictures, (Stupid analogies) General relativity is like curved rubbers sheet (this is awful because they don’t follow even approximately the same equation) in teaching.
There are good stories [Like (Good Story) Your trig story (Good analogy) The microwave-euler’s number analogy is good analogy (they follow the approximately same equation) or (Good pictures) Various proof without words ]
This separation between good and stupid should be made explicit, other wise they could seriously puzzle the student, tricking them into believing they had understood something but actually they don’t.
Great point. I don’t like insipid analogies which are just awkward restatements of the technical definitions. A good analogy should summarize the essence of an idea, similar to a caricature artist.
It is puzzling to extract (or make) good analogies. Do you use some rule of thumb to check whether an analogy is insipid or good ?
An analogy should tell you more about the system than when you started. For example, seeing imaginary numbers as 2d rotations makes you wonder if you can have rotations in higher dimensions, using “even better” imaginary numbers (which is the case).
Thanks. You may try out reading the “Lockharts lament”, its easily available online for free (25 pages PDF)
Good example! That’s exactly what happened after I learnt about complex numbers in high school: I started looking for extensions of the √(-1) idea. I found that in the 1800s, Hamilton had created quaternions, and was able to read his original works on the subject at the Melbourne University library.
Quaternions use three different imaginary numbers: i, j, and k, which all square to -1, but whose pairwise products are equal to +/- the other one. A few years later, I was seeing quaternions applied to physics.
And they’re just the tip of the “hypercomplex” iceberg!
Hi, Kalid!
Great job!!!
If only … teachers understood how to learn! Most are still clueless after
(a) doing it (sorta) themselves and
(b) centuries of trying to understand the process.
What’s so great about this article – and your guide to the discrete Fourier transform – is that you have a psychological understanding of learners-as-people, rather than learners-as-empty-vessels to drizzle drivel into!
My experiences in teaching have taught me, beyond a shadow of doubt, that a motivated learner WILL learn, but an unmotivated one CAN’T. I’ll be back to read some more of your entertaining and intelligent writing.
[And maybe one day somebody (you?) will actually explain clearly just how a tensor differs from a vector or a matrix – I’ve only been looking for that explanation for 49 years to date! :-( ]
Thanks for the feedback! Exactly, Socrates said a teaching a student is about lighting a fire, not filling a vessel. Facts without true insight and enthusiasm are lifeless.
I’d like to learn more about tensors myself :).
“Priority #1 for any class is: Do not create hate for the subject.”
————– I found this funny because this is exactly what now-adays most courses/instructors do!
The courses are taught in a horrible way that people would never even want to even think about what’s been taught.
Good analogy should come from the lowest level of understanding: the fundamentals. Once you know things well like you know your palm, you are able to crystalize it in the most concise way capturing the essentials.
But unfortunately, I found nowadays people abuse the usage of analogies simply because they don’t quite understand the essence. And they try to come up with stuff from their old experiences convincing themselves. And then such twisted version of knowledge gets disseminated and everyone is quoting another’s twisted version. Eventually you find people are talking different things, speaking of different languages.
That’s making everyday communication so difficult: you have questions, but you don’t know where you don’t know. I have partially twisted answers, and when we talk, it’s becoming mission impossible. And most cases the communication is ineffective and waste of time.
I have a example of bad analogies ( I think): Schrödinger’s cat for superposition.
The analogy that cat is both dead-alive trying to convince me that it is both a 0 and a 1 confuse me. I cannot understand how you get a computer to do calculations if it is both 0 and 1?
To me, I think it is just that you can have 4 different states to represent numbers, and computers can do calculations much faster, but the problem is you will not always get correct answers, so you have to do some error correction.
I have been begging for clarifications by emailing to quantum computing departments in lots of universities, but nobody answers my question.
Can anybody here shed some lights????
The world is at two extremes:
1) technical experts lost in mechanics and details, unable to explain things easily— it is bad because these people fail to share their knowledge with others, because knowledge is secretly encrypted.
2) Braggers appear knowledgeable covering up their ignore ance by wrapping up details in a insipid or even twisted format—- it is fatal because this group of people are vocal, and they will lead to erroneous information multiply like virus.
We need more passionate learners, seeking truth, seeking real understanding to be vocal, spread the real knowledge, inspiring each other.
Kalid, there should be another honest guide for teaching! Would be sort of a mirror of this, but basically, once you are in a role in teaching, people will assume you with deep and broad knowledge and they will trust you, so they will take every word you say seriously. Once they don’t understand, most people will blame on themselves therefore don’t even have the courage to ask a question! I used to blame myself being stupid if i don’t understand something, but now, i am confident in saying that a lot of times there could be a common confusion deserving more discussion, so instead of pretending and hiding the issues, why don’t we be honest in both learning and teaching so that we will be crystal clear about what we really understand, and we will know where we don’t understand and that might suffice another round of digging. This is a healthy learning process as you are constantly resolving puzzles as you are building them.
But currently, I see we are just constantly building puzzles without even realizing it. The danger is there are tons of confusions out there, and when people confused get together, each with their own twisted version of the picture, as they start chatting, I feel it is like ducks talking to chicken: it is absolutely a chaos, nobody knows what others are saying, but everyone is confused. And everyone is more confused after the discussion…