Vector Calculus: Understanding the Dot Product

I think of the dot product as directional multiplication. Multiplication goes beyond repeated counting: it's applying the essence of one item to another. (For example, complex multiplication is rotation, not repeated counting.)

When dealing with simple growth rates, multiplication scales one rate by another:

"3 x 4" can mean "Take your 3x growth and make it 4x as large, to get 12x"

When dealing with vectors ("directional growth"), there's a few operations we can do:

Add vectors: Accumulate the growth contained in several vectors.
Multiply by a constant: Make an existing vector stronger (in the same direction).
Dot product: Apply the directional growth of one vector to another. The result is how much stronger we've made the original vector (positive, negative, or zero).

Today we'll build our intuition for how the dot product works.

Getting the Formula Out of the Way

You've seen the dot product equation everywhere:

$\displaystyle{\vec{a} \cdot \vec{b} = a_x \cdot b_x + a_y \cdot b_y = |\vec{a}||\vec{b}|\cos(\theta) }$

And also the justification: "Well Billy, the Law of Cosines (you remember that, don't you?) says the following calculations are the same, so they are." Not good enough -- it doesn't click! Beyond the computation, what does it mean?

The goal is to apply one vector to another. The equation above shows two ways to accomplish this:

Rectangular perspective: combine x and y components
Polar perspective: combine magnitudes and angles

The "this stuff = that stuff" equation just means "Here are two equivalent ways to 'directionally multiply' vectors".

Seeing Numbers as Vectors

Let's start simple, and treat 3 x 4 as a dot product:

$\displaystyle{(3, 0) \cdot (4,0)}$

The number 3 is "directional growth" in a single dimension (the x-axis, let's say), and 4 is "directional growth" in that same direction. 3 x 4 = 12 means we get 12x growth in a single dimension. Ok.

Now, suppose 3 and 4 refer to different dimensions. Let's say 3 means "triple your bananas" (x-axis) and 4 means "quadruple your oranges" (y-axis). Now they're not the same type of number: what happens when apply growth (use the dot product) in our "bananas, oranges" universe?

(3,0) means "Triple your bananas, destroy your oranges"
(0,4) means "Destroy your bananas, quadruple your oranges"

Applying (0,4) to (3,0) means "Destroy your banana growth, quadruple your orange growth". But (3, 0) had no orange growth to begin with, so the net result is 0 ("Destroy all your fruit, buddy").

$\displaystyle{(3, 0) \cdot (0, 4) = 0}$

See how we're "applying" and not simply adding? With regular addition, we smush the vectors together: (3,0) + (0, 4) = (3, 4) [a vector which triples your oranges and quadruples your bananas].

"Application" is different. We're mutating the original vector based on the rules of the second. And the rules of (0, 4) are "Destroy your banana growth, and quadruple your orange growth." When applied to something with only bananas, like (3, 0), we're left with nothing.

The final result of the dot product process can be:

Zero: we don't have any growth in the original direction
Positive number: we have some growth in the original direction
Negative number: we have negative (reverse) growth in the original direction

Understanding the Calculation

"Applying vectors" is still a bit abstract. I think "How much energy/push is one vector giving to the other?". Here's how I visualize it:

Rectangular Coordinates: Component-by-component overlap

Like multiplying complex numbers, see how each x- and y-component interacts:

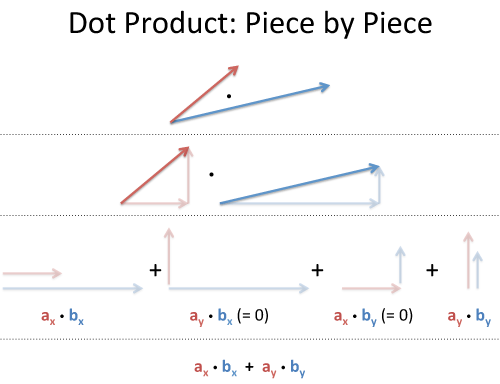
We list out all four combinations (x with x, y with x, x with y, y with y). Since the x- and y-coordinates don't affect each other (like holding a bucket sideways under a waterfall -- nothing falls in), the total energy absorbtion is absorbtion(x) + absorbtion(y):

$\displaystyle{\vec{a} \cdot \vec{b} = a_x \cdot b_x + a_y \cdot b_y}$

Polar coordinates: Projection

The word "projection" is so sterile: I prefer "along the path". How much energy is actually going in our original direction?

Here's one way to see it:

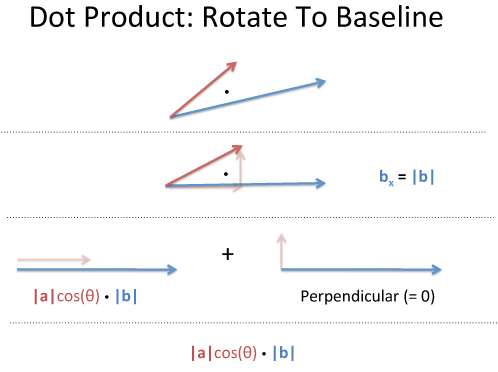
Take two vectors, a and b. Rotate our coordinates so b is horizontal: it becomes (|b|, 0), and everything is on this new x-axis. What's the dot product now? (It shouldn't change just because we tilted our head).

Well, vector a has new coordinates (a1, a2), and we get:

$\displaystyle{a1 \cdot |\vec{b}| + a2 \cdot 0 = a1 \cdot |\vec{b}|}$

a1 is really "What is the x-coordinate of a, assuming b is the x-axis?". That is |a|cos(θ), aka the "projection":

$\displaystyle{\vec{a} \cdot \vec{b} = |\vec{a}|\cos(\theta)|\vec{b}|}$

Analogies for the Dot Product

The common interpretation is "geometric projection", but it's so bland. Here's some analogies that click for me:

Energy Absorbtion

One vector are solar rays, the other is where the solar panel is pointing (yes, yes, the normal vector). Larger numbers mean stronger rays or a larger panel. How much energy is absorbed?

Energy = Overlap in direction * Strength of rays * Size of panel
$\displaystyle{\text{Energy} = \cos(\theta) \cdot |a| \cdot |b|}$

If you hold your panel sideways to the sun, no rays hit (cos(θ) = 0).

Photo credit

But... but... solar rays are leaving the sun, and the panel is facing the sun, and the dot product is negative when vectors are opposed! Take a deep breath, and remember the goal is to embrace the analogy (besides, physicists lose track of negative signs all the time).

Mario-Kart Speed Boost

In Mario Kart, there are "boost pads" on the ground that increase your speed (Never played? I'm sorry.)

Photo source

Imagine the red vector is your speed (x and y direction), and the blue vector is the orientation of the boost pad (x and y direction). Larger numbers are more power.

How much boost will you get? For the analogy, imagine the pad gives a speed bonus like this:

If you come in going 0, you'll get nothing. (If you are dropped onto the pad, there's no boost.)
If you cross the pad perpendicularly, you'll get 0 benefit. (Just like the banana obliteration, there's 0x boost in the perpendicular direction.)
If our direction and pad are aligned, our x-speed contributes an x-boost, and our y-speed gives us a y-boost:

$\displaystyle{\text{boost effect} = speed_x \cdot boost_x + speed_y \cdot boost_y}$

Neat, eh? Another way to see it: your incoming speed is $|a|$, and the max boost is $|b|$. The percentage of boost you actually get (based on how you're lined up) is $\cos(\theta)$, for an overal boost of $|a||b|\cos(\theta)$, which is the dot product.

Fruit Stand Analogy

Let's say your store sells apples, bananas, and clementines. They cost \$1, \$2, and \$3 each, respectively.

A customer wants to buy 2 apples, 3 bananas, and 4 clementines. What does it cost?

cost = (A quantity) * (A price) + (B quantity) * (B price) + (C quantity) * (C price) 
cost = 2*1 + 3*2 + 4*3 = 20

This is the dot product between the "quantity" vector and the "price" vector! We're multiplying the matching entries and getting the total. We ignore entries that don't "make sense" to multiply (why should the banana quantity and clementine price impact each other?).

Physics Physics Physics

The dot product appears all over physics: some field (electric, gravitational) is pulling on some particle. We'd love to multiply, and we could if everything were lined up. But that's never the case, so we take the dot product to account for potential differences in direction.

It's all a useful generalization: Integrals are "multiplication, taking changes into account" and the dot product is "multiplication, taking direction into account".

And what if your direction is changing? Why, take the integral of the dot product, of course!

Onward and Upward

Don't settle for "Dot product is the geometric projection, justified by the law of cosines". Find the analogies that click for you! Happy math.