Intuitive Understanding of Sine Waves

Sine waves confused me. Yes, I can mumble "SOH CAH TOA" and draw lines within triangles. But what does it mean?

I was stuck thinking sine had to be extracted from other shapes. A quick analogy:

You: Geometry is about shapes, lines, and so on.

Alien: Oh? Can you show me a line?

You (looking around): Uh... see that brick, there? A line is one edge of that brick.

Alien: So lines are part of a shape?

You: Sort of. Yes, most shapes have lines in them. But a line is a basic concept on its own: a beam of light, a route on a map, or even--

Alien: Bricks have lines. Lines come from bricks. Bricks bricks bricks.

Most math classes are exactly this. "Circles have sine. Sine comes from circles. Circles circles circles."

Argh! No - circles are one example of sine. In a sentence: Sine is a natural sway, the epitome of smoothness: it makes circles "circular" in the same way lines make squares "square".

Let's build our intuition by seeing sine as its own shape, and then understand how it fits into circles and the like. Onward!

Sine vs Lines

Remember to separate an idea from an example: squares are examples of lines. Sine clicked when it became its own idea, not "part of a circle."

Let's observe sine in a simulator:

Hubert will give the tour:

Click start. Go, Hubert go! Notice that smooth back and forth motion? That's Hubert, but more importantly (sorry Hubert), that's sine! It's natural, the way springs bounce, pendulums swing, strings vibrate... and many things move.
Change "vertical" to "linear". Big difference -- see how the motion gets constant and robotic, like a game of pong?

Let's explore the differences with video:

Linear motion is constant: we go a set speed and turn around instantly. It's the unnatural motion in the robot dance (notice the linear bounce with no slowdown vs. the strobing effect).
Sine changes its speed: it starts fast, slows down, stops, and speeds up again. It's the enchanting smoothness in liquid dancing (human sine wave and natural bounce).

Unfortunately, textbooks don't show sine with animations or dancing. No, they prefer to introduce sine with a timeline (try setting "horizontal" to "timeline"):

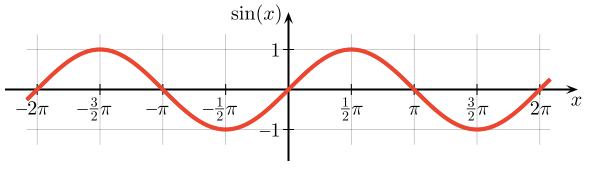(source)

Egads. This is the schematic diagram we've always been shown. Does it give you the feeling of sine? Not any more than a skeleton portrays the agility of a cat. Let's watch sine move and then chart its course.

The Unavoidable Circle

Circles have sine. Yes. But seeing the sine inside a circle is like getting the eggs back out of the omelette. It's all mixed together!

Let's take it slow. In the simulation, set Hubert to vertical:none and horizontal: sine*. See him wiggle sideways? That's the motion of sine. There's a small tweak: normally sine starts the cycle at the neutral midpoint and races to the max. This time, we start at the max and fall towards the midpoint. Sine that "starts at the max" is called cosine, and it's just a version of sine (like a horizontal line is a version of a vertical line).

Ok. Time for both sine waves: put vertical as "sine" and horizontal as "sine*". And... we have a circle!

A horizontal and vertical "spring" combine to give circular motion. Most textbooks draw the circle and try to extract the sine, but I prefer to build up: start with pure horizontal or vertical motion and add in the other.

Quick Q & A

A few insights I missed when first learning sine:

Sine really is 1-dimensional

Sine wiggles in one dimension. Really. We often graph sine over time (so we don't write over ourselves) and sometimes the "thing" doing sine is also moving, but this is optional! A spring in one dimension is a perfectly happy sine wave.

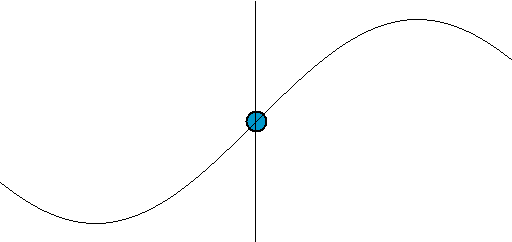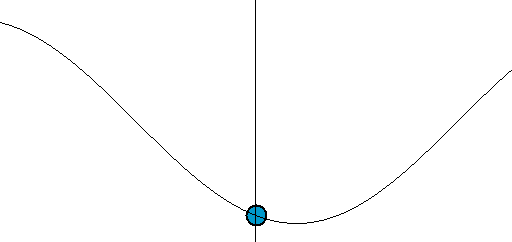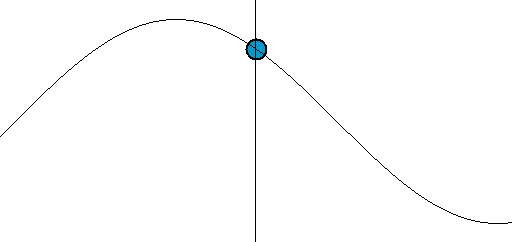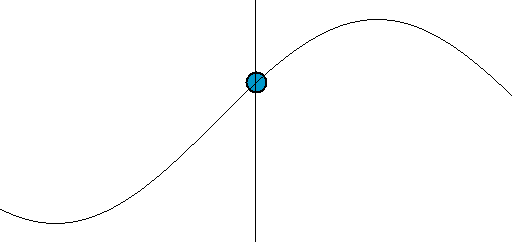
(Source: Wikipedia, try not to get hypnotized.)

Circles are an example of two sine waves

Circles and squares are a combination of basic components (sines and lines). The circle is made from two connected 1-d waves, each moving the horizontal and vertical direction.

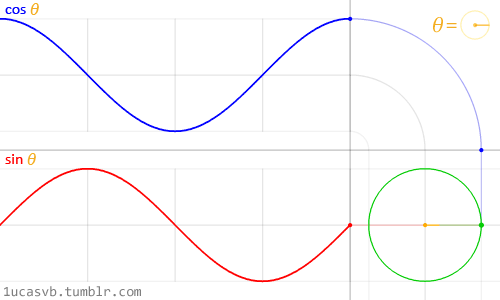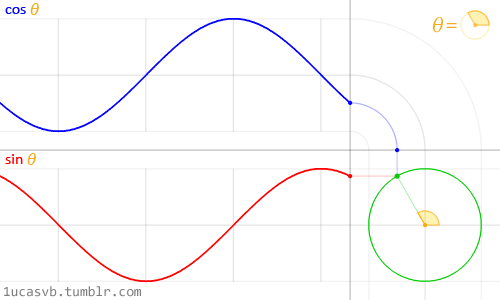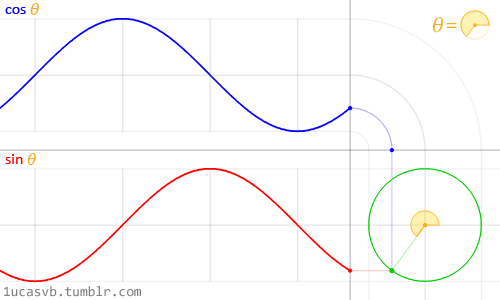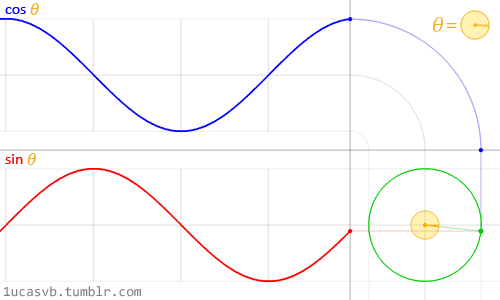
(Source http://1ucasvb.tumblr.com/)

But remember, circles aren't the origin of sines any more than squares are the origin of lines. They're examples of two sine waves working together, not their source.

What do the values of sine mean?

Sine cycles between -1 and 1. It starts at 0, grows to 1.0 (max), dives to -1.0 (min) and returns to neutral. I also see sine like a percentage, from 100% (full steam ahead) to -100% (full retreat).

What's is the input 'x' in sin(x)?

Tricky question. Sine is a cycle and x, the input, is how far along we are in the cycle.

Let's look at lines:

You're traveling on a square. Each side takes 10 seconds.
After 1 second, you are 10% complete on that side
After 5 seconds, you are 50% complete
After 10 seconds, you finished the side

Linear motion has few surprises. Now for sine (focusing on the "0 to max" cycle):

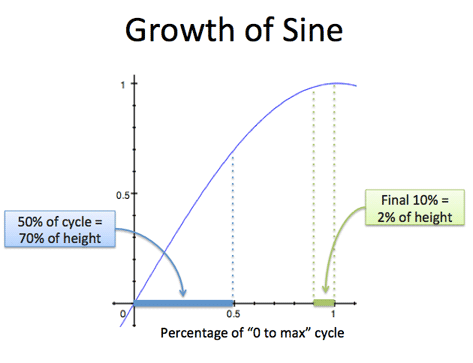
We're traveling on a sine wave, from 0 (neutral) to 1.0 (max). This portion takes 10 seconds.
After 5 seconds we are... 70% complete! Sine rockets out of the gate and slows down. Most of the gains are in the first 5 seconds
It takes 5 more seconds to get from 70% to 100%. And going from 98% to 100% takes almost a full second!

Despite our initial speed, sine slows so we gently kiss the max value before turning around. This smoothness makes sine, sine.

For the geeks: Press "show stats" in the simulation. You'll see the percent complete of the total cycle, mini-cycle (0 to 1.0), and the value attained so far. Stop, step through, and switch between linear and sine motion to see the values.

Quick quiz: What's further along, 10% of a linear cycle, or 10% of a sine cycle? Sine. Remember, it barrels out of the gate at max speed. By the time sine hits 50% of the cycle, it's moving at the average speed of linear cycle, and beyond that, it goes slower (until it reaches the max and turns around).

So x is the 'amount of your cycle'. What's the cycle?

It depends on the context.

Basic trig: 'x' is degrees, and a full cycle is 360 degrees
Advanced trig: 'x' is radians (they are more natural!), and a full cycle is going around the unit circle (2*pi radians)

Play with values of x here:

But again, cycles depend on circles! Can we escape their tyranny?

Pi without Pictures

Imagine a sightless alien who only notices shades of light and dark. Could you describe pi to it? It's hard to flicker the idea of a circle's circumference, right?

Let's step back a bit. Sine is a repeating pattern, which means it must... repeat! It goes from 0, to 1, to 0, to -1, to 0, and so on.

Let's define pi as the time sine takes from 0 to 1 and back to 0. Whoa! Now we're using pi without a circle too! Pi is a concept that just happens to show up in circles:

Sine is a gentle back and forth rocking
Pi is the time from neutral to max and back to neutral
n * Pi (0 * Pi, 1 * pi, 2 * pi, and so on) are the times you are at neutral
2 * Pi, 4 * pi, 6 * pi, etc. are full cycles

Aha! That is why pi appears in so many formulas! Pi doesn't "belong" to circles any more than 0 and 1 do -- pi is about sine returning to center! A circle is an example of a shape that repeats and returns to center every 2*pi units. But springs, vibrations, etc. return to center after pi too!

Question: If pi is half of a natural cycle, why isn't it a clean, simple number?

Let's answer a question with a question. Why does a 1x1 square have a diagonal of length $\sqrt{2} = 1.414...$ (an irrational number)?

It's philosophically inconvenient when nature doesn't line up with our number system. I don't have a good intuition. My hunch is simple rules (1x1 square + Pythagorean Theorem) can still lead to complex outcomes.

How fast is sine?

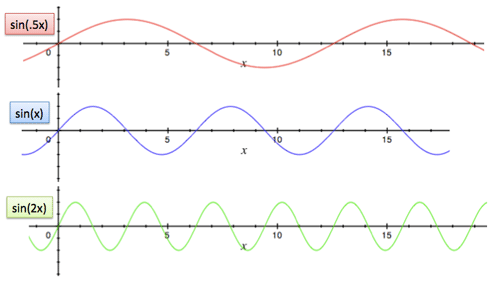
I've been tricky. Previously, I said "imagine it takes sine 10 seconds from 0 to max". And now it's pi seconds from 0 to max back to 0? What gives?

sin(x) is the default, off-the-shelf sine wave, that indeed takes pi units of time from 0 to max to 0 (or 2*pi for a complete cycle)
sin(2x) is a wave that moves twice as fast
sin(0.5x) is a wave that moves twice as slow

So, we use sin(n*x) to get a sine wave cycling as fast as we need. Often, the phrase "sine wave" is referencing the general shape and not a specific speed.

Part 2: Understanding the definitions of sine

That's a brainful -- take a break if you need it. Hopefully, sine is emerging as its own pattern. Now let's develop our intuition by seeing how common definitions of sine connect.

Definition 1: The height of a triangle / circle!

Sine was first found in triangles. You may remember "SOH CAH TOA" as a mnemonic

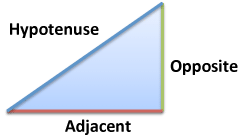
SOH: Sine is Opposite / Hypotenuse
CAH: Cosine is Adjacent / Hypotenuse
TOA: Tangent is Opposite / Adjacent

For a right triangle with angle x, sin(x) is the length of the opposite side divided by the hypotenuse. If we make the hypotenuse 1, we can simplify to:

Sine = Opposite
Cosine = Adjacent

And with more cleverness, we can draw our triangles with hypotenuse 1 in a circle with radius 1:

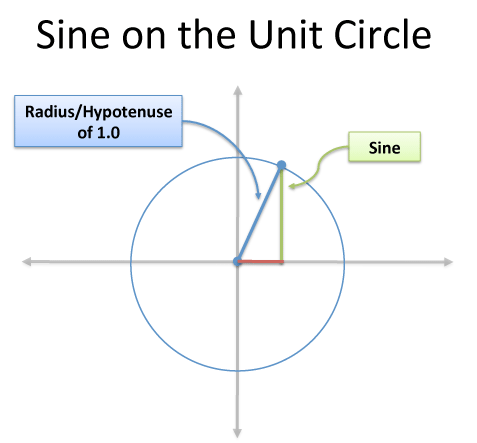
Voila! A circle containing all possible right triangles (since they can be scaled up using similarity). For example:

sin(45) = .707
Lay down a 10-foot pole and raise it 45 degrees. It is 10 * sin(45) = 7.07 feet off the ground
An 8-foot pole would be 8 * sin(45) = 5.65 feet

These direct manipulations are great for construction (the pyramids won't calculate themselves). Unfortunately, after thousands of years we start thinking the meaning of sine is the height of a triangle. No no, it's a shape that shows up in circles (and triangles).

Realistically, for many problems we go into "geometry mode" and start thinking "sine = height" to speed through things. That's fine -- just don't get stuck there.

Definition 2: The infinite series

I've avoided the elephant in the room: how in blazes do we actually calculate sine!? Is my calculator drawing a circle and measuring it?

Glad to rile you up. Here's the circle-less secret of sine:

Sine is acceleration opposite to your current position

Using our bank account metaphor: Imagine a perverse boss who gives you a raise the exact opposite of your current bank account! If you have \$50 in the bank, then your raise next week is \$50. Of course, your income might be \$75/week, so you'll still be earning some money \$75 - \$50 for that week), but eventually your balance will decrease as the "raises" overpower your income.

But never fear! Once your account hits negative (say you're at \$50), then your boss gives a legit \$50/week raise. Again, your income might be negative, but eventually the raises will overpower it.

This constant pull towards the center keeps the cycle going: when you rise up, the "pull" conspires to pull you in again. It also explains why neutral is the max speed for sine: If you are at the max, you begin falling and accumulating more and more "negative raises" as you plummet. As you pass through then neutral point you are feeling all the negative raises possible (once you cross, you'll start getting positive raises and slowing down).

By the way: since sine is acceleration opposite to your current position, and a circle is made up of a horizontal and vertical sine... you got it! Circular motion can be described as "a constant pull opposite your current position, towards your horizontal and vertical center".

Geeking Out With Calculus

Let's describe sine with calculus. Like e, we can break sine into smaller effects:

Start at 0 and grow at unit speed
At every instant, get pulled back by negative acceleration

How should we think about this? See how each effect above changes our distance from center:

Our initial kick increases distance linearly: y (distance from center) = x (time taken)
At any moment, we feel a restoring force of $-x$. We integrate twice to turn negative acceleration into distance:

$\displaystyle{ \iint -x = \frac{-x^3}{3!} }$

Seeing how acceleration impacts distance is like seeing how a raise hits your bank account. The "raise" must change your income, and your income changes your bank account (two integrals "up the chain").

So, after "x" seconds we might guess that sine is "x" (initial impulse) minus $\frac{x^3}{3!}$ (effect of the acceleration):

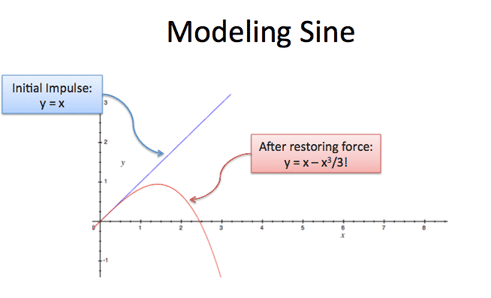
Something's wrong -- sine doesn't nosedive! With e, we saw that "interest earns interest" and sine is similar. The "restoring force" changes our distance by $\frac{-x^3}{3!}$, which creates another restoring force to consider. Consider a spring: the pull that yanks you down goes too far, which shoots you downward and creates another pull to bring you up (which again goes too far). Springs are crazy!

We need to consider every restoring force:

$y = x$ is our initial motion, which creates a restoring force of impact...
$y = \frac{-x^3}{3!}$ which creates a restoring force of impact...
$y = \frac{x^5}{5!}$ which creates a restoring force of impact...
$y = \frac{-x^7}{7!}$ which creates a restoring force of impact...

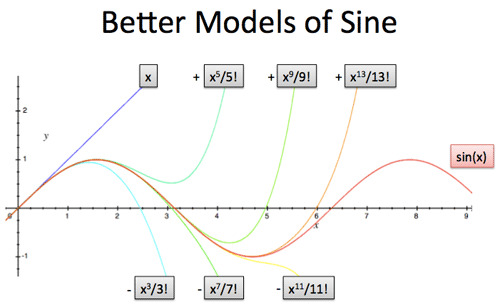
Just like e, sine can be described with an infinite series:

$\displaystyle{\sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + ... }$

I saw this formula a lot, but it only clicked when I saw sine as a combination of an initial impulse and restoring forces. The initial push (y = x, going positive) is eventually overcome by a restoring force (which pulls us negative), which is overpowered by its own restoring force (which pulls us positive), and so on.

A few fun notes:

Consider the "restoring force" like "positive or negative interest". This makes the sine/e connection in Euler's formula easier to understand. Sine is like e, except sometimes it earns negative interest. There's more to learn here :).
For very small angles, "y = x" is a good guess for sine. We just take the initial impulse and ignore any restoring forces.

The Calculus of Cosine

Cosine is just a shifted sine, and is fun (yes!) now that we understand sine:

Sine: Start at 0, initial impulse of y = x (100%)
Cosine: Start at 1, no initial impulse

So cosine just starts off... sitting there at 1. We let the restoring force do the work:

$\displaystyle{y = 1 - \frac{x^2}{2!}}$

Again, we integrate -1 twice to get $\frac{-x^2}{2!}$. But this kicks off another restoring force, which kicks off another, and before you know it:

$\displaystyle{\cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + ...}$

Definition 3: The differential equation

We've described sine's behavior with specific equations. A more succinct way (equation):

$\displaystyle{y'' = -y}$

This beauty says:

Our current position is y
Our acceleration (2nd derivative, or y'') is the opposite of our current position (-y)

Both sine and cosine make this true. I first hated this definition; it's so divorced from a visualization. I didn't realize it described the essence of sine, "acceleration opposite your position".

And remember how sine and e are connected? Well, $e^x$ can be be described by (equation):

$\displaystyle{y'' = y}$

The same equation with a positive sign ("acceleration equal to your position")! When sine is "the height of a circle" it's really hard to make the connection to e.

One of my great mathematical regrets is not learning differential equations. But I want to, and I suspect having an intuition for sine and e will be crucial.

Summing it up

The goal is to move sine from some mathematical trivia ("part of a circle") to its own shape:

Sine is a smooth, swaying motion between min (-1) and max (1). Mathematically, you're accelerating opposite your position. This "negative interest" keeps sine rocking forever.
Sine happens to appear in circles and triangles (and springs, pendulums, vibrations, sound...).
Pi is the time from neutral to neutral in sin(x). Similarly, pi doesn't "belong" to circles, it just happens to show up there.

Let sine enter your mental toolbox (Hrm, I need a formula to make smooth changes...). Eventually, we'll understand the foundations intuitively (e, pi, radians, imaginaries, sine...) and they can be mixed into a scrumptious math salad. Enjoy!

Appendix

Using this approach, Alistair MacDonald made a great tutorial with code to build your own sine and cosine functions.