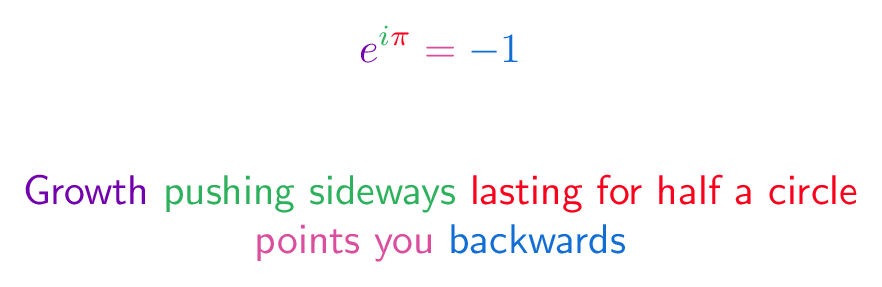Euler's identity seems baffling:
![]()
It emerges from a more general formula:
![]()
Yowza -- we're relating an imaginary exponent to sine and cosine! And somehow plugging in pi gives -1? Could this ever be intuitive?
Not according to 1800s mathematician Benjamin Peirce:
It is absolutely paradoxical; we cannot understand it, and we don't know what it means, but we have proved it, and therefore we know it must be the truth.
Argh, this attitude makes my blood boil! Formulas are not magical spells to be memorized: we must, must, must find an insight. Here's mine:
Euler's formula describes two equivalent ways to move in a circle.
That's it? This stunning equation is about spinning around? Yes -- and we can understand it by building on a few analogies:
- Starting at the number 1, see multiplication as a transformation that changes the number: $1 \cdot e^{i \pi}$
- Regular exponential growth continuously increases 1 by some rate for some time period; imaginary exponential growth continuously rotates 1 for some time period
- Growing for "pi" units of time means going pi radians around a circle
- Therefore, $e^{i \pi}$ means starting at 1 and rotating pi (halfway around a circle) to get to -1
That's the high-level view, let's dive into the details. By the way, if someone tries to impress you with $e^{i \pi} = -1$, ask them about i to the i-th power. If they can't think it through, Euler's formula is still a magic spell to them.
Update: While writing, I thought a video might help explain the ideas more clearly:
Understanding cos(x) + i * sin(x)
The equals sign is overloaded. Sometimes we mean "set one thing to another" (like x = 3) and others we mean "these two things describe the same concept" (like $\sqrt{-1} = i$).
Euler's formula is the latter: it gives two formulas which explain how to move in a circle. If we examine circular motion using trig, and travel x radians:
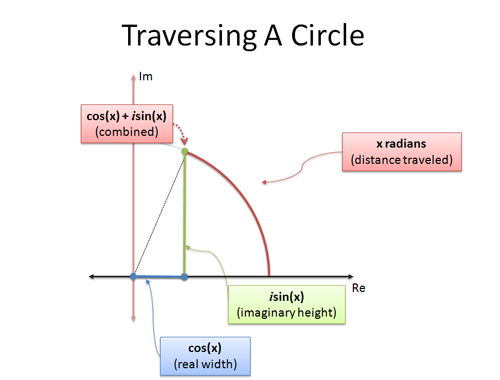
- cos(x) is the x-coordinate (horizontal distance)
- sin(x) is the y-coordinate (vertical distance)
The statement
![]()
is a clever way to smush the x and y coordinates into a single number. The analogy "complex numbers are 2-dimensional" helps us interpret a single complex number as a position on a circle.
When we set x to $\pi$, we're traveling $\pi$ units along the outside of the unit circle. Because the total circumference is $2\pi$, plain old $\pi$ is halfway around, putting us at -1.
Neato: The right side of Euler's formula ($\cos(x) + i \sin(x)$) describes circular motion with imaginary numbers. Now let's figure out how the e side of the equation accomplishes it.
What is Imaginary Growth?
Combining x- and y- coordinates into a complex number is tricky, but manageable. But what does an imaginary exponent mean?
Let's step back a bit. When I see $3^4$, I think of it like this:
- 3 is the end result of growing instantly (using e) at a rate of ln(3). In other words: $3 = e^{\ln(3)}$
- $3^4$ is the same as growing to 3, but then growing for 4x as long. So $3^4 = e^{\ln(3) \cdot 4} = 81$
Instead of seeing numbers on their own, you can think of them as something e had to "grow to". Real numbers, like 3, give an interest rate of ln(3) = 1.1, and that's what e "collects" as it's going along, growing continuously.
Regular growth is simple: it keeps "pushing" a number in the same, real direction it was going. 3 × 3 pushes in the original direction, making it 3 times larger (9).
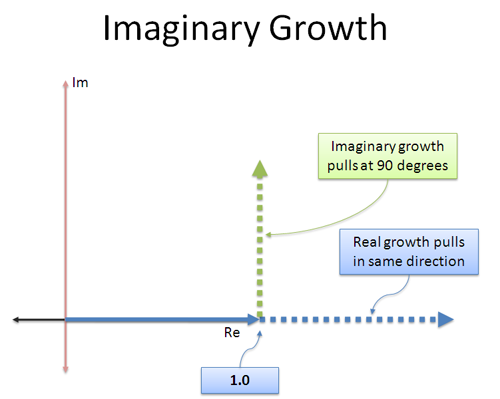
Imaginary growth is different: the "interest" we earn is in a different direction! It's like a jet engine that was strapped on sideways -- instead of going forward, we start pushing at 90 degrees.
The neat thing about a constant orthogonal (perpendicular) push is that it doesn't speed you up or slow you down -- it rotates you! Taking any number and multiplying by i will not change its magnitude, just the direction it points.
Intuitively, here's how I see continuous imaginary growth rate: "When I grow, don't push me forward or back in the direction I'm already going. Rotate me instead."
But Shouldn't We Spin Faster and Faster?
I wondered that too. Regular growth compounds in our original direction, so we go 1, 2, 4, 8, 16, multiplying 2x each time and staying in the real numbers. We can consider this $e^{\ln(2)x}$, which means grow instantly at a rate of ln(2) for "x" seconds.
And hey -- if our growth rate was twice as fast, 2ln(2) vs ln(2), it would look the same as growing for twice as long (2x vs x). The magic of e lets us swap rate and time; 2 seconds at ln(2) is the same growth as 1 second at 2ln(2).
Now, imagine we have some purely imaginary growth rate (Ri) that rotates us until we reach i, or 90 degrees upward. What happens if we double that rate to 2Ri, will we spin off the circle?
Nope! Having a rate of 2Ri means we just spin twice as fast, or alternatively, spin at a rate of R for twice as long, but we're staying on the circle. Rotating twice as long means we're now facing 180 degrees.
Once we realize that some exponential growth rate can take us from 1 to i, increasing that rate just spins us more. We'll never escape the circle.
However, if our growth rate is complex (a+bi vs Ri) then the real part (a) will grow us like normal, while the imaginary part (bi) rotates us. But let's not get fancy: Euler's formula, $e^{ix}$, is about the purely imaginary growth that keeps us on the circle (more later).
A Quick Sanity Check
While writing, I had to clarify a few questions for myself:
Why use $e^x$, aren't we rotating the number 1?
e represents the process of starting at 1 and growing continuously at 100% interest for 1 unit of time.
When we write e we're capturing that entire process in a single number -- e represents all the whole rigmarole of continuous growth. So really, $e^x$ is saying "start at 1 and grow continuously at 100% for x seconds", and starts from 1 like we want.
But what does i as an exponent do?
For a regular exponent like $3^4$ we ask:
- What is the implicit growth rate? We're growing from 1 to 3 (the base of the exponent).
- How do we change that growth rate? We scale it by 4x (the power of the exponent).
We can convert our growth into "e" format: our instantaneous rate is ln(3), and we increase it to ln(3) * 4. Again, the power of the exponent (4) just scaled our growth rate.
![]()
When the top exponent is i (as in $3^i$), we just multiply our implicit growth rate by i. So instead of growing at plain old ln(3), we're growing at ln(3) * i.
![]()
The top part of the exponent modifies the implicit growth rate of the bottom part.
The Nitty Gritty Details
Let's take a closer look. Remember this definition of e:
![]()
That $\frac{100\%}{n}$ represents the portion interest we earned in each microscopic period. We assumed the interest rate was 100% in the real dimension -- but what if it were 100% in the imaginary direction?
![]()
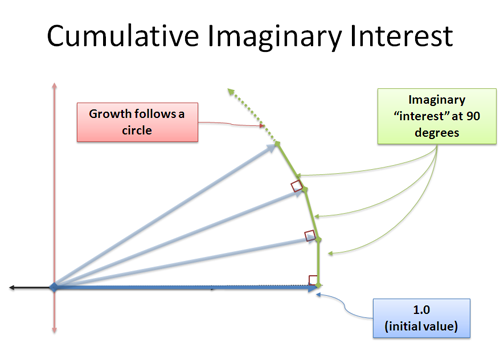
Now, our newly formed interest adds to us in the 90-degree direction. Surprisingly, this does not change our length -- this is a tricky concept, because it appears to make a triangle where the hypotenuse must be larger. We're dealing with a limit, and the extra distance is within the error margin we specify. This is something I want to tackle another day, but take my word: continuous perpendicular growth will rotate you. This is the heart of sine and cosine, where your change is perpendicular to your current position, and you move in a circle.
We apply i units of growth in infinitely small increments, each pushing us at a 90-degree angle. There is no "faster and faster" rotation - instead, we crawl along the perimeter a distance of |i| = 1 (magnitude of i).
And hey -- the distance crawled around a circle is an angle in radians! We've found another way to describe circular motion!
To get circular motion: Change continuously by rotating at 90-degree angle (aka imaginary growth rate).
So, Euler's formula is saying "exponential, imaginary growth traces out a circle". And this path is the same as moving in a circle using sine and cosine in the imaginary plane.
In this case, the word "exponential" is confusing because we travel around the circle at a constant rate. In most discussions, exponential growth is assumed to have a cumulative, compounding effect.
Some Examples
You don't really believe me, do you? Here's a few examples, and how to think about them intuitively.
Example: $e^i$
Where's the x? Ah, it's just 1. Intuitively, without breaking out a calculator, we know that this means "travel 1 radian along the unit circle". In my head, I see "e" trying to grow 1 at 100% all in the same direction, but i keeps moving the ball and forces "1" to grow along the edge of a circle:
![]()
Not the prettiest number, but there it is. Remember to put your calculator in radian mode when punching this in.
Example: $3^i$
This is tricky -- it's not in our standard format. But remember, ![]()
We want an initial growth of 3x at the end of the period, or an instantaneous rate of ln(3). But, the i comes along and changes that rate of ln(3) to "i * ln(3)":
![]()
We thought we were going to transform at a regular rate of ln(3), a little faster than 100% continuous growth since e is about 2.718. But oh no, i spun us around: now we're transforming at an imaginary rate which means we're just rotating about. If i was a regular number like 4, it would have made us grow 4x faster. Now we're growing at a speed of ln(3), but sideways.
We should expect a complex number on the unit circle -- there's nothing in the growth rate to increase our size. Solving the equation:
![]()
So, rather than ending up "1" unit around the circle (like $e^i$) we end up ln(3) units around.
Example: $i^i$
A few months ago, this would have had me tears. Not today! Let's break down the transformations:
![]()
We start with 1 and want to change it. Like solving $3^i$, what's the instantaneous growth rate represented by i as a base?
Hrm. Normally we'd do ln(x) to get the growth rate needed to reach x at the end of 1 unit of time. But for an imaginary rate? We need to noodle this over.
In order to start with 1 and grow to i we need to start rotating at the outset. How fast? Well, we need to get 90 degrees (pi/2 radians) in 1 unit of time. So our rate is $i \frac{\pi}{2}$. Remember our rate must be imaginary since we're rotating, not growing! Plain old $\frac{\pi}{2}$ is about 1.57 and results in regular growth.
This should make sense: to turn 1.0 to i at the end of 1 unit, we should rotate $\frac{\pi}{2}$ radians (90 degrees) in that amount of time. So, to get "i" we can use $e^{i \frac{\pi}{2}}$.
![]()
Phew. That describes i as the base. How about the exponent?
Well, the other i tells us to change our rate -- yes, that rate we spent so long figuring out! So rather than rotating at a speed of $i \frac{\pi}{2}$, which is what a base of i means, we transform the rate to:
![]()
The i's cancel and make the growth rate real again! We rotated our rate and pushed ourselves into the negative numbers. And a negative growth rate means we're shrinking -- we should expect $i^i$ to make things smaller. And it does:
![]()
Tada! (Search "i^i" on Google to use its calculator)
Take a breather: You can intuitively figure out how imaginary bases and imaginary exponents should behave. Whoa.
And as a bonus, you figured out ln(i) -- to make $e^x$ become i, make e rotate $\frac{\pi}{2}$ radians.
![]()
Example: (i^i)^i
A double imaginary exponent? If you insist. First off, we know what our growth rate will be inside the parenthesis:
![]()
We get a negative (shrinking) growth rate of -pi/2. And now we modify that rate again by i:
![]()
And now we have a negative rotation! We're going around the circle a rate of $-\frac{\pi}{2}$ per unit time. How long do we go for? Well, there's an implicit "1" unit of time at the very top of this exponent chain; the implied default is to go for 1 time unit (just like $e = e^1$). 1 time unit gives us a rotation of $-\frac{\pi}{2}$ radians (-90 degrees) or -i!
![]()
And, just for kicks, if we squared that crazy result:
![]()
It's "just" twice the rotation: 2 is a regular number so doubles our rotation rate to a full -180 degrees in a unit of time. Or, you can look at it as applying -90 degree rotation twice in a row.
At first blush, these are really strange exponents. But with our analogies we can take them in stride.
Complex Growth
We can have real and imaginary growth at the same time: the real portion scales us up, and the imaginary part rotates us around:
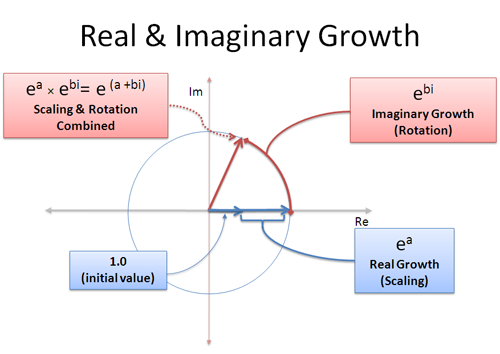
A complex growth rate like (a + bi) is a mix of real and imaginary growth. The real part a, means "grow at 100% for a seconds" and the imaginary part b means "rotate for b seconds". Remember, rotations don't get the benefit of compounding since you keep 'pushing' in a different direction -- rotation adds up linearly.
With this in mind, we can represent any point on any sized circle using (a+bi)! The radius is $e^a$ and the angle is determined by $e^{bi}$. It's like putting the number in the expand-o-tron for two cycles: once to grow it to the right size (a seconds), another time to rotate it to the right angle (b seconds). Or, you could rotate it first and then grow!
Let's say we want to know the growth amount to get to 6 + 8i. This is really asking for the natural log of an imaginary number: how do we grow e to get (6 + 8i)?
- Radius: How big of a circle do we need? Well, the magnitude is $\sqrt{6^2 + 8^2} = \sqrt{100} = 10$. Which means we need to grow for ln(10) = 2.3 seconds to reach that amount.
- Amount to rotate: What's the angle of that point? We can use arctan to figure it out: atan(8/6) = 53 degrees = .93 radian.
- Combine the result: ln(6+8i) = 2.3 + .93i
That is, we can reach the random point (6 + 8i) if we use $e^{2.3 + .93i}$.
Why Is This Useful?
Euler's formula gives us another way to describe motion in a circle. But we could already do that with sine and cosine -- what's so special?
It's all about perspective. Sine and cosine describe motion in terms of a grid, plotting out horizontal and vertical coordinates.

Euler's formula uses polar coordinates -- what's your angle and distance? Again, it's two ways to describe motion:
- Grid system: Go 3 units east and 4 units north
- Polar coordinates: Go 5 units at an angle of 53.13 degrees
Depending on the problem, polar or rectangular coordinates are more useful. Euler's formula lets us convert between the two to use the best tool for the job. Also, because $e^{ix}$ can be converted to sine and cosine, we can rewrite formulas in trig as variations on e, which comes in very handy (no need to memorize sin(a+b), you can derive it -- more another day). And it's beautiful that every number, real or complex, is a variation of e.
But utility, schmutility: the most important result is the realization that baffling equations can become intuitive with the right analogies. Don't let beautiful equations like Euler's formula remain a magic spell -- build on the analogies you know to see the insights inside the equation.
Happy math.
Appendix
The screencast was fun, and feedback is definitely welcome. I think it helps the ideas pop, and walking through the article helped me find gaps in my intuition.
References:
- Brian Slesinsky has a neat presentation on Euler's formula
- Visual Complex Analysis has a great discussion on Euler's formula -- see p. 10 in the Google Book Preview
- I did a talk on Math and Analogies which explains Euler's Identity more visually:
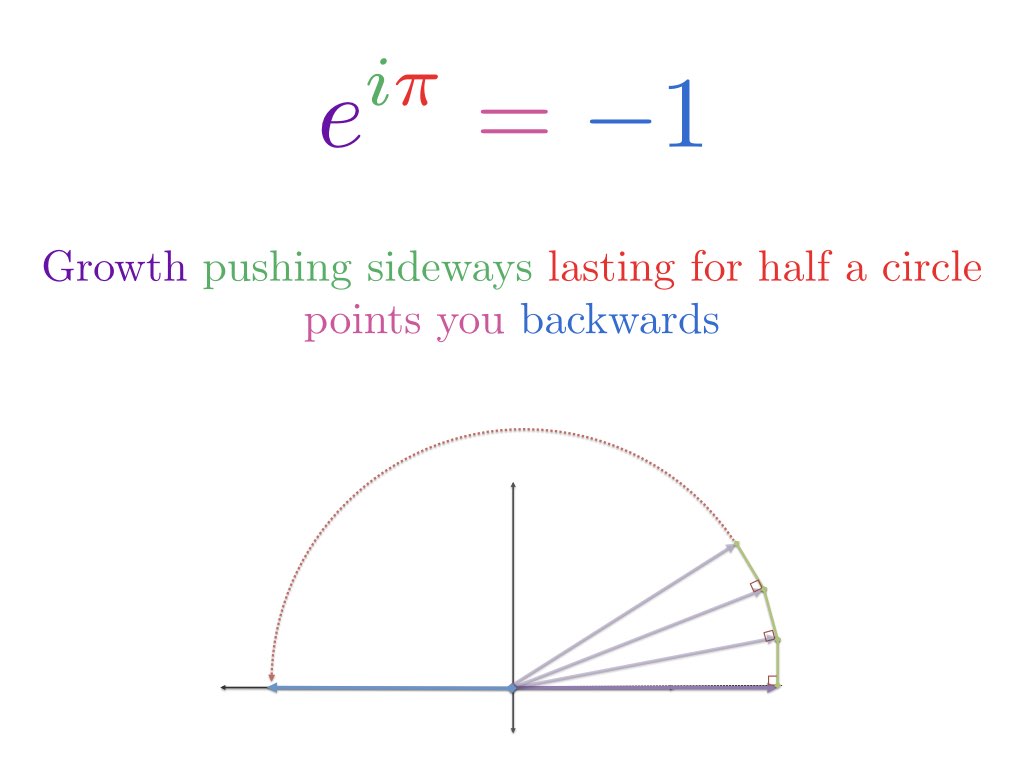
Other Posts In This Series
- A Visual, Intuitive Guide to Imaginary Numbers
- Intuitive Arithmetic With Complex Numbers
- Understanding Why Complex Multiplication Works
- Intuitive Guide to Angles, Degrees and Radians
- Intuitive Understanding Of Euler's Formula
- An Interactive Guide To The Fourier Transform
- Intuitive Guide to Convolution
- Intuitive Understanding of Sine Waves
- An Intuitive Guide to Linear Algebra
- A Programmer's Intuition for Matrix Multiplication
- Imaginary Multiplication vs. Imaginary Exponents
- Intuitive Guide to Hyperbolic Functions